标签:
1.查找(search) 是指在数据集合中寻找满足某种条件的数据元素的过程。用于查找的数据集合则称为 查找表(search table)。查找表中的数据元素类型是一致的,并且有能够唯一标识出元素的 关键字(keyword)。如果从查找表中找出了关键字等于某个给定值的数据元素,则称为 查找成功,否则称 查找不成功。
通常对查找表有 4 种操作:
①查找:在查找表中查看某个特定的记录是否存在
②检索:查找某个特定记录的各种属性
③插入:将某个不存在的数据元素插入到查找表中
④删除:从查找表中删除某个特定元素
如果对查找表只执行前两种操作,则称这类查找表为 静态查找表(static search table)。静态查找表建立以后,就不能再执行插入或删除操作,查找表也不再发生变化。对应的,如果对查找表还要执行后两种操作,则称这类查找表为 动态查找表(dynamic search table)。本章我们要介绍的查找算法都是针对静态查找表的,比如顺序查找、折半查找、分块查找等;而对于动态查找表,往往使用二叉平衡树、B-树或哈希表来处理。
对于各种各样的查找算法,我们要如何比较他们的优劣呢?通常,我们使用 平均查找长度(average search length, ASL)来衡量查找算法的性能。对于含有 n 个元素的查找表,定义查找成功的平均查找长度为
ASL=∑i=0PiCi
其中 P?i?? 是搜索查找表中第 i 个记录的概率,并且 ∑i=0Pi=1(通常我们认为每个元素被查找的概率相等,即Pi=1/n )。Ci?? 是指搜索查找表中第 i 个元素时直到查找成功为止,表中元素的比较次数。考虑到查找不成功的情况,查找算法的平均查找长度应该是查找成功的平均查找长度和查找不成功的平均查找长度之和。通常我们在说平均查找长度时,不考虑查找不成功的情况。
比如一个给定的查找表 A = [1, 2, 3, 4, 5]A=[1,2,3,4,5],其中每个 Pi=1/5??。若对于某个查找算法,每个元素到查找成功为止的比较次数C=[1, 2, 3, 4, 5]C=[1,2,3,4,5]。则该查找算法的平均查找长度为3。
2.顺序查找
顺序查找(又称线性查找,sequential search),是指在线性表中进行的查找算法。顺序查找算法是最直观的一种查找算法,它从线性表的一端出发,逐个比对关键字是否满足给定的条件。
顺序查找按照查找表中数据的性质,分为对一般的无序线性表的顺序查找和对按关键字有序的线性表的顺序查找。下面我们分别对这两种查找算法进行讲解。


大致是之前查找不成功的平均查找长度 nn 的一半,效率提升还是很明显的。当然,这种方法只适用于有序表。
顺序查找的实现
1 #include <iostream> 2 #include <cstring> 3 using namespace std; 4 class Vector { 5 private: 6 int size, length; 7 int *data; 8 public: 9 Vector(int input_size) { 10 size = input_size; 11 length = 0; 12 data = new int[size]; 13 } 14 ~Vector() { 15 delete[] data; 16 } 17 bool insert(int loc, int value) { 18 if (loc < 0 || loc > length) { 19 return false; 20 } 21 if (length >= size) { 22 expand(); 23 } 24 for (int i = length; i > loc; --i) { 25 data[i] = data[i - 1]; 26 } 27 data[loc] = value; 28 length++; 29 return true; 30 } 31 void expand() { 32 int * old_data = data; 33 size = size * 2; 34 data = new int[size]; 35 for (int i = 0; i < length; ++i) { 36 data[i] = old_data[i]; 37 } 38 delete[] old_data; 39 } 40 int search(int value) { //有序表上顺序查找算法 41 for(int i=0;i<length;i++){ 42 if(data[i]==value){ //逐个比较,若相等则返回下标 43 return i; 44 } 45 else if(data[i]>value){ //此处为有序表,因此大于可判断查找不成功 46 return -1; 47 } 48 } 49 return -1; //value比表中所有值都大,查找不成功 50 } 51 bool remove(int index) { 52 if (index < 0 || index >= length) { 53 return false; 54 } 55 for (int i = index + 1; i < length; ++i) { 56 data[i - 1] = data[i]; 57 } 58 length = length - 1; 59 return true; 60 } 61 void print() { 62 for (int i = 0; i < length; ++i) { 63 if (i > 0) { 64 cout << " "; 65 } 66 cout << data[i]; 67 } 68 cout << endl; 69 } 70 }; 71 int main() { 72 Vector a(100); 73 a.insert(0, 2); 74 a.insert(1, 4); 75 a.insert(2, 6); 76 a.insert(3, 8); 77 a.insert(4, 10); 78 79 cout << a.search(4) << endl; 80 cout << a.search(5) << endl; 81 return 0; 82 }
对于有序表,查找不成功的平均查找长度是可以优化的。那么对于查找成功的情况,能不能利用有序表的关键字有序的特性,对效率进行优化呢?
3.二分查找


下面我们来一起分析一下折半查找算法的平均查找长度 ASLASL。为了直观,我们把有序表折半查找的过程用一棵 二叉判定树(binary decision tree, BDT) 来表示,如下图:
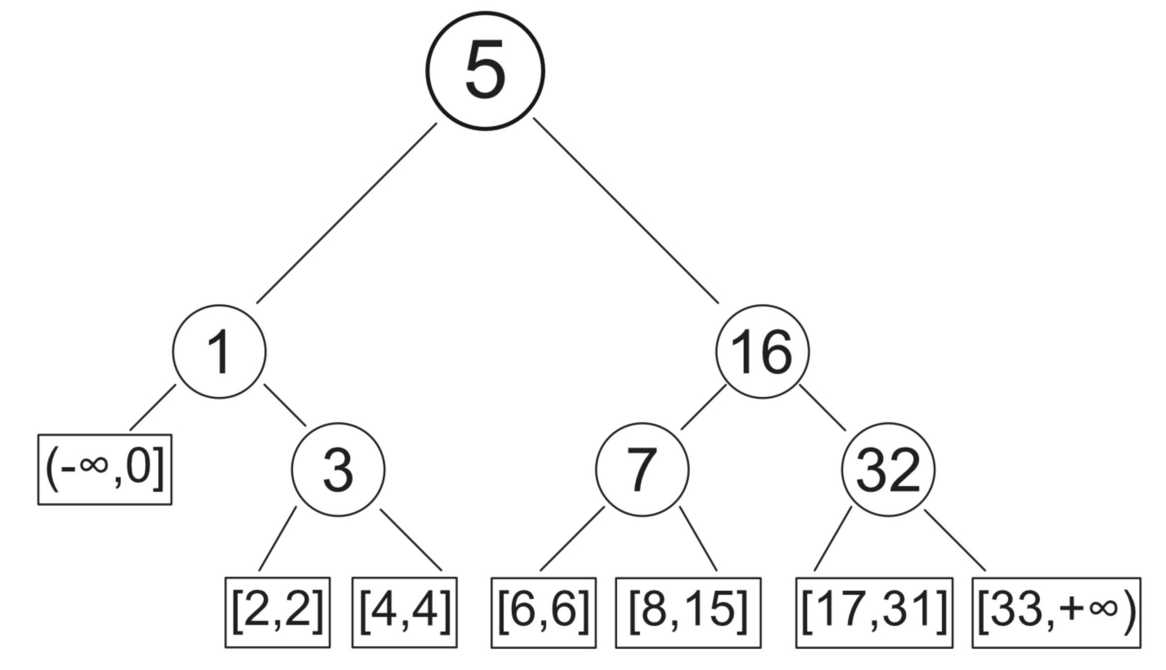
通过这样一棵树,我们可以很容易计算出折半查找算法查找成功的平均查找长度:
ASL = 1 *(1/6) + 2 *(2/6) + 3 *(3/6) = 7/3
而如果用顺序查找算法,平均查找长度为"
ASL = (n+1)/2 = 3 > 7/3??
可以看出,折半查找是比顺序查找更高效的查找算法。
无论查找成功还是查找不成功,在有序表中查找某个关键字的过程就是从根节点出发走到该关键字对应结点的路径,而路径的长度就对应着查找长度。与此同时,这个路径长度也对应着该结点在树上的深度。由于树的深度是 O(logn)+1,所以每次查找不成功的比较次数不会超过O(logn) +1。
因此,折半查找的时间复杂度为 O(logn),明显优于时间复杂度为 O(n)的顺序查找算法。不过一定要注意,折半查找只适用于关键字有序的顺序表,无序的线性表如果想使用折半查找要先进行排序操作,而链表因为无法随机存取所以没有办法使用折半查找。
二分查找的代码实现:
1 #include <iostream> 2 #include <cstring> 3 using namespace std; 4 class Vector { 5 private: 6 int size, length; 7 int *data; 8 public: 9 Vector(int input_size) { 10 size = input_size; 11 length = 0; 12 data = new int[size]; 13 } 14 ~Vector() { 15 delete[] data; 16 } 17 bool insert(int loc, int value) { 18 if (loc < 0 || loc > length) { 19 return false; 20 } 21 if (length >= size) { 22 expand(); 23 } 24 for (int i = length; i > loc; --i) { 25 data[i] = data[i - 1]; 26 } 27 data[loc] = value; 28 length++; 29 return true; 30 } 31 void expand() { 32 int * old_data = data; 33 size = size * 2; 34 data = new int[size]; 35 for (int i = 0; i < length; ++i) { 36 data[i] = old_data[i]; 37 } 38 delete[] old_data; 39 } 40 int search(int value) { 41 int left=0,right=length-1; 42 while(left<=right){ 43 int mid=(left+right)/2; 44 if(data[mid]==value){ 45 return mid; 46 } 47 else if(data[mid]<value){ 48 left=mid+1; 49 } 50 else{ 51 right=mid-1; 52 } 53 } 54 return -1; 55 } 56 bool remove(int index) { 57 if (index < 0 || index >= length) { 58 return false; 59 } 60 for (int i = index + 1; i < length; ++i) { 61 data[i - 1] = data[i]; 62 } 63 length = length - 1; 64 return true; 65 } 66 void print() { 67 for (int i = 0; i < length; ++i) { 68 if (i > 0) { 69 cout << " "; 70 } 71 cout << data[i]; 72 } 73 cout << endl; 74 } 75 }; 76 int main() { 77 Vector a(100); 78 a.insert(0, 2); 79 a.insert(1, 4); 80 a.insert(2, 6); 81 a.insert(3, 8); 82 a.insert(4, 10); 83 84 cout << a.search(4) << endl; 85 cout << a.search(5) << endl; 86 return 0; 87 }
关于left<=right何时加等号何时不加,一般来说,有left或right=mid时不能加等号,不然容易陷入死循环。
标签:
原文地址:http://www.cnblogs.com/Reindeer/p/5693327.html