深入理解关系型数据库(一)

标签：

　　前言：是否写了很多年的SQL查询，仍然不知道这个大盒子里怎么运作的? 如果你感兴趣，不妨读读本文。

　　每当说到关系型数据库时，我总感觉少点什么。各式各样的数据库被到处使用，从轻量的SQLite到强大的Teradata。但是，几乎没有一篇文章来解释这些关系型数据库到底是怎样工作的。你使用谷歌搜索“关系型数据库的运行原理”，基本上搜不到什么结果。现在，如果你有接触到比较流行的技术（Big Data, NoSQL或者JavaScript），你却可以找到一些比较深入的介绍它们原理的文章。

　　难道关系型的数据库太老土和无聊了吗？以至于在大学课堂，论文和专业书籍以外的地方都没人去深入研究。

　　作为一个开发者，我很厌恶我常使用但又不理解的东西。数据库被使用了40多年，一定有它的原因。这些年来，我花费了数百个小时来理解这个我每天使用的怪黑盒子。关系型数据库很有趣因为它基于一些很有用处和被重复使用的概念，如果你一直想弄懂关系型数据库是怎么工作的，但是一直都没有足够的时间去深入研究，那么你应该读读这篇博客。

　　尽管文章的标题再直白不过，本文的目的不在于教你怎么使用数据库，因此，你首先应该知道怎么写一些基本的CRUD查询，要不然你可能无法理解此篇文章。知道这些知识就足够了，其余的留给我来给你解释。

　　我将从时间复杂度开始说起，有些人肯定很讨厌这些概念，但是如果没有时间复杂度的概念，你就无法理解数据库中的妙处。尽管“时间复杂度”是一个庞大的主题，我只会关注其中我认为关键的地方：数据库处理一个SQL查询。我将解释数据库底层的一些概念这样当你读完本篇文章的时候，你就能大致理解数据库底层是怎么运作的了。

　　本篇技术文章涉及到很多算法和数据结构，你可以慢慢阅读它。一些概念可能比较难以理解，你可以跳过这部分也能大致理解数据库的运行原理。

　　本篇文章主要分为3个部分：

　　> 底层和上层的数据库组件

　　> 基本的查询优化过程

　　> 事务和缓冲池的管理

-----------------------------------------------------------------------------

　　　　　　　　　　                    目录

     1 基本算法

　　　　1.1 O(1)对比O(n²)

　　　　　　1.1.1 概念

　　　　　　1.1.2 示例

　　　　　　1.1.3 深入

　　　　1.2 归并排序

　　　　　　1.2.1 归并

　　　　　　1.2.2 拆分阶段

　　　　　　1.2.3 排序阶段

　　　　　　1.2.4 归并排序的威力

　　　　1.3 数组，树和哈希表

　　　　　　1.3.1 数组

　　　　　　1.3.2 树和数据库索引

　　　　　　1.3.3 哈希表

　　2 数据库概览

　　3 客户端管理器

　　4 查询管理器

　　　　4.1 查询解析器

　　　　4.2 查询重写器

　　　　4.3 统计分析器

　　　　4.4 查询优化器

　　　　　　4.4.1 索引

　　　　　　4.4.2 访问路径

　　　　　　4.4.3 连接运算符

　　　　　　4.4.4 简化的示例

　　　　　　4.4.5 动态规划，贪心算法和启发式

　　　　　　4.4.6 优化器

　　　　　　4.4.7 查询计划缓存

　　　　4.5 查询执行器

　　5 数据管理器

　　　　5.1 缓存管理器

　　　　　　5.1.1 预先获取

　　　　　　5.1.2 缓存替换策略

　　　　　　5.1.3 写缓存

　　　　5.2 事务管理器

　　　　　　5.2.1 ACID事务

　　　　　　5.2.2 并发控制

　　　　　　5.2.3 锁管理

　　　　　　5.2.4 日志管理

　　6 总结

-----------------------------------------------------------------------------

基本算法

　　很久以前（在一个遥远的星系..），开发者们得知道他们写的代码有多少条指令。他们必须得充分理解他们的算法和数据结构因为他们浪费不起那些慢机器上的CPU和内存。

　　这部粉，我将介绍一些基本的算法，因为他们对理解数据至关重要。我也将介绍下数据库索引的概念。

O(1)对比O(n²)

　　现在，大部分程序员不怎么关系时间复杂度了...他们是对的！

　　但是，当处理大数据量的时候（不是千级别）或者程序需要在毫秒级别上作斗争时，那理解这个概念就变得很重要了。数据库在这两方面都有做处理，我不会浪费你很多时间来介绍这个概念，它将帮助我们理解基于时间开销的优化。

概念

　　时间复杂度是用来衡量一个算法处理给定的数据需要花多长时间。计算机科学家们使用数学符号大O来描述。这个符号使用一个函数来描述一个算法对给你的输入需要多少次操作。

　　例如，当算法的复杂度是O（some_function()）,它的意思就是，这个算法需要some_function(amount_of_data)次操作来完成这个任务。

　　重要的不在于amount_of_data, 而在于当amount_of_data增长时，时间复杂度的增长情况，时间复杂度不会给出具体数值，但是让你了解大致的时间开销。

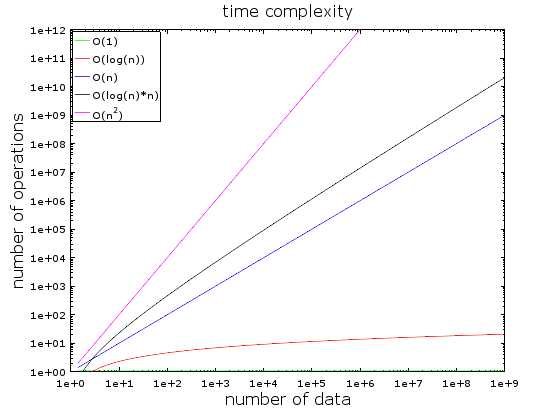
　　在这个图表中，你可以看到不同时间复杂度的演变情况，我使用对数来绘制它们。

　　> O(1)或常量时间基本保持不变(不然也不会被称之为常量时间)

　　> O(log(n))在亿级别的数据量时依然很小

　　> 最差的复杂度是O(n²), 复杂度随数据量的增长而剧烈上升。

示例

　　当数据量很小的时候，O(1)和O(n²)基本没啥区别，例如对于处理2000个元素算法。

　　> O(1)的算法需要1次操作

　　> O(log(n))的算法需要7次操作

　　> O(n)的算法需要2000次操作

　　> O(n*log(n))的算法需要14000次操作

　　> O(n²)的算法需要4000000次操作

　　O(1)和O(n²)的区别很大但实际上只差了2毫秒，你一眨眼的功夫。确实，现在处理器每秒钟可以做数千万次操作。所以现在对于很多IT项目来说，性能和优化都不是问题。

　　而对于处理1000000个元素的算法而言， O(n²)的时间都可以喝杯咖啡了，如果数据量在大一个数量级都可以睡一觉了。

深入

　　> 查找一个好的哈希表的时间复杂度是O(1)

　　> 查找一个好的平衡二叉树的时间复杂度是O(log(n))

　　> 查找一个数组中的元素的时间复杂度时O(n)

　　> 最佳的排序算法的时间复杂度是O(n*log(n))

　　> 最差的排序算法的时间复杂度是O(n²)

　　Note：在下一部分中，我们将看到这些算法和数据结构。

       时间复杂度有三种类型，平均，最佳，最差。我们一般讨论的是最差情况下的时间复杂度。算法的复杂度还涉及到内存消耗和I/O读写。

　　还有一些更差的时间复杂度如n⁴, 3ⁿ, n!, nⁿ等，这里不一一介绍。

归并排序

　　当你需要排序一个集合的时候你会怎么做？什么？使用sort()函数...好吧，回答得好。但对于数据库而言你需要理解sort函数在其中是怎么运作的。

　　有很多好的排序算法，在这里只介绍归并排序。你现在可能无法理解为什么排序这么重要，但是当你读完查询优化那一部分的时候就理解了，这也会帮助我们理解数据库中一个比较常用的连接操作，合并连接。

归并

　　像有些算法一样，归并排序基于这样一个小把戏：即归并2个长度为N/2的有序数组为1个长度为N的有序数组需要N次操作。这种操作成为归并。

　　让我们看看如下的一个简单的例子：

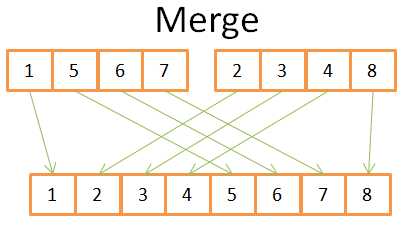
　　在图中可以看到为了构造得到含8个元素的有序数组，你只需要遍历一次2个含4个元素的数组。因为它们都是有序的：

　　1）比较在2个数组中的当前位置的元素（当前=第一个，在最开始的时候）

　　2）将其中最小的放到结果数组中

　　3）当前位置在最小元素的数组中后移一位

　　4）重复步骤1，2，3直到某个数组的最后一个位置

　　5）将另外一个数组余下的元素全添加到结果数组中

　　当我们理解了这个小把戏，接下来看看我的归并排序的伪代码。

array mergeSort(array a)
   if(length(a)==1)
      return a[0];
   end if

   //recursive calls
   [left_array right_array] := split_into_2_equally_sized_arrays(a);
   array new_left_array := mergeSort(left_array);
   array new_right_array := mergeSort(right_array);

   //merging the 2 small ordered arrays into a big one
   array result := merge(new_left_array,new_right_array);
   return result;

　　归并排序将问题分解成子问题，在解决子问题的过程中解决原问题（这种思想叫分治法，分而治之），如果你不理解这种算法，不要着急，我第一次见到时也不理解。我将这种算法划分为两个阶段以帮助你理解：

　　> 分：将数组划分为更小的数组

　　> 治：小的排序数组通过归并合成一个大的数组

拆分阶段

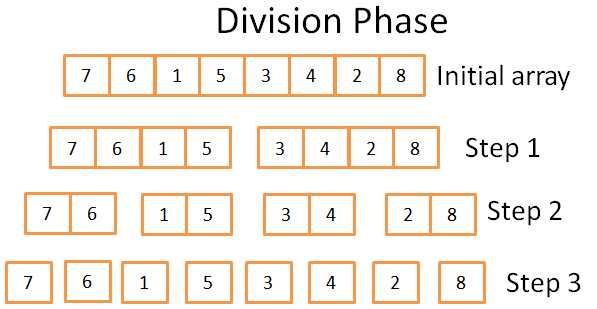
　　在拆分阶段，数组通过3步被分成了只包含一个元素的数组，这个过程一共有log(N)（N=8，所以log(N)=3）.

　　我是怎么知道的？

　　我是天才！ 换句话说，数学。过程是在每个步骤的时候将数组分为2份，步骤数即为数组被分成两半的次数，即以2为底的对数定义。

排序阶段

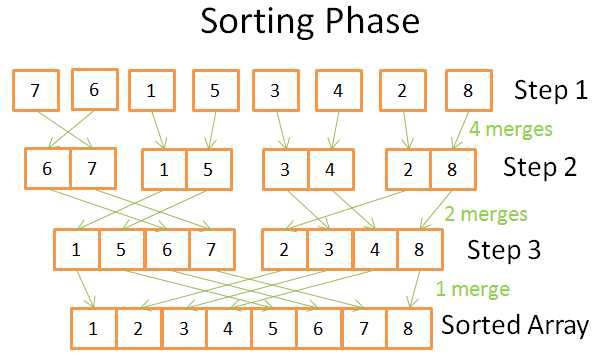
　　在排序阶段，从含有单个元素的数组开始，在每个步骤的时候都使用归并操作合并数组，每一次都花费N=8次操作：

　　> 第一步，你需要4次归并，每次2个操作

　　> 第二步，你需要2次归并，每次4次操作

　　> 第三步，你需要1次归并，8次操作

　　因为需要log(N)步，所以总的时间复杂度为N * log(N)

归并排序的威力

　　为什么这个算法这么有用呢？

　　> 你没有创建新的数组而是直接修改原数组，这样减少了内存的占用。这种算法称为 in-place，原地修改。

　　> 为了使用更少的内存和硬盘空间以减少磁盘I/O，将当前需要处理的数据部分载入到内存中。这样当你需要排序好几G的表的时候只需要100M的内存空间。这种排序方式称为外部排序。

　　> 你可以在多个处理器/线程/服务器上处理它。例如，分布式的归并排序是Hadoop的关键组件之一。

　　这种排序算法在数据库中最常用，如果你想了解更多，你可以阅读各种排序算法在数据库中使用时的优劣对比。research paper

数组，树和哈希表

　　当你理解了时间复杂度和排序后，接下来我们介绍3中数据结构，因为它们是现代数据库的基础，接着也会介绍下数据库索引。

数组　

　　二维的数组是最简单的数据结构之一，一个数据库表可以看作是一个数组，例如：

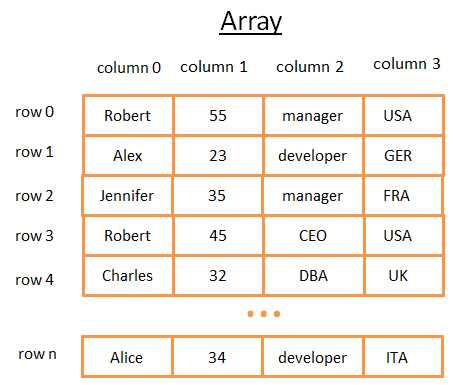
　　这个二维数组是由行和列构成的：

　　> 每一行代表一个主题

　　> 列描述了这个主题的特征

　　> 每一列存储了特定类型的数据（integer, string, date ...）

　　这种方式用来存储和可视化数据时很好，但是当你需要找到特定值的时候很麻烦。

　　例如，如果你想找到所有在UK工作的人，你必须去每一行找到匹配UK的行。这将花费你N次操作（N是数据的行数），这种方式还不错，但是有更快的方法吗？树

　　Note：大多数现代数据库提供了高级的数组来存储表如堆构建的表或索引构建的表，但是这仍然没有解决快速查找列中满足某些条件的行的问题。

树和数据库索引

　　二叉搜索树是满足如下特性的二叉树，每个节点存储的值：

　　> 比左子树存储的值要大

　　> 比右子树存储的值要小

　　如图：

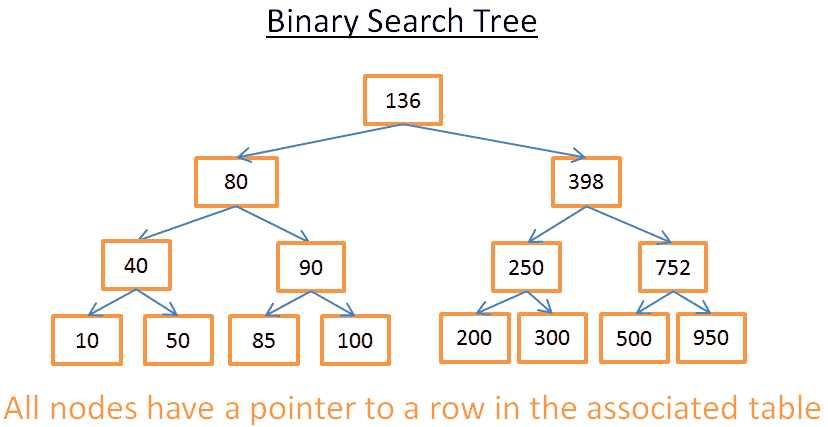
　　这棵树有N=15个元素，假设我们需要查找208：

　　> 从根节点开始，其值是136，因为136<208，所以往其右子树继续查找。

　　> 因为398>208,所以往其左子树继续查找。

　　> 因为250>208，所以往其左子树继续查找。

　　> 因为200<208，所以往其右子树继续查找。由于200不存在右子树，所以值208不存在该树中。

　　现在，我们以查找40为例

　　> 从值为136的根节点开始，136>40，所以往其左子树继续查找。

　　> 因为80>40,所以从其左子树继续查找。

　　> 40=40,查找成功，节点存在。找到该节点所在行的id，然后去查表。

　　> 知道行id让我们可以精确的知道数据在表的位置，这样我们可以立马得到它。

　　最后，一共花费了树的深度次查找，为log(N)，还不赖！

　　回到我们之前的问题，它很抽象。一个string代表了某个人所在的国家，假设二叉搜索树中包含了表中名为“country”的列：如果你想查找谁在UK工作，首先你从树中找到代表UK的节点，然后找到所在行的位置。

　　这种查找方式花费log(N)次操作而不是N次，你可以把它理解为数据库索引。

　　你可以为任意组合的列构建树的索引，只要你有个函数来比较键值，这样你就可以建立一个基于键值的顺序。

　　B+树索引

　　尽管从树中查找特定值很方便，但是当你要查找大小在两个值之间的元素时会很麻烦。你将需要花费O(N)的时间来检查每个节点的值是否在2个给定的值之间（例如，通过树的中序遍历）,并且因为需要读整棵树所以磁盘I/O效率也不好。要找到一种高效的方式来进行范围查询，现代的数据库使用了在B+树。在B+树中：

　　>  处于最低层的节点（叶子节点）存储信息（对应的表的行所在的位置）
　　> 其他节点在查找时调整以定位到其对的节点

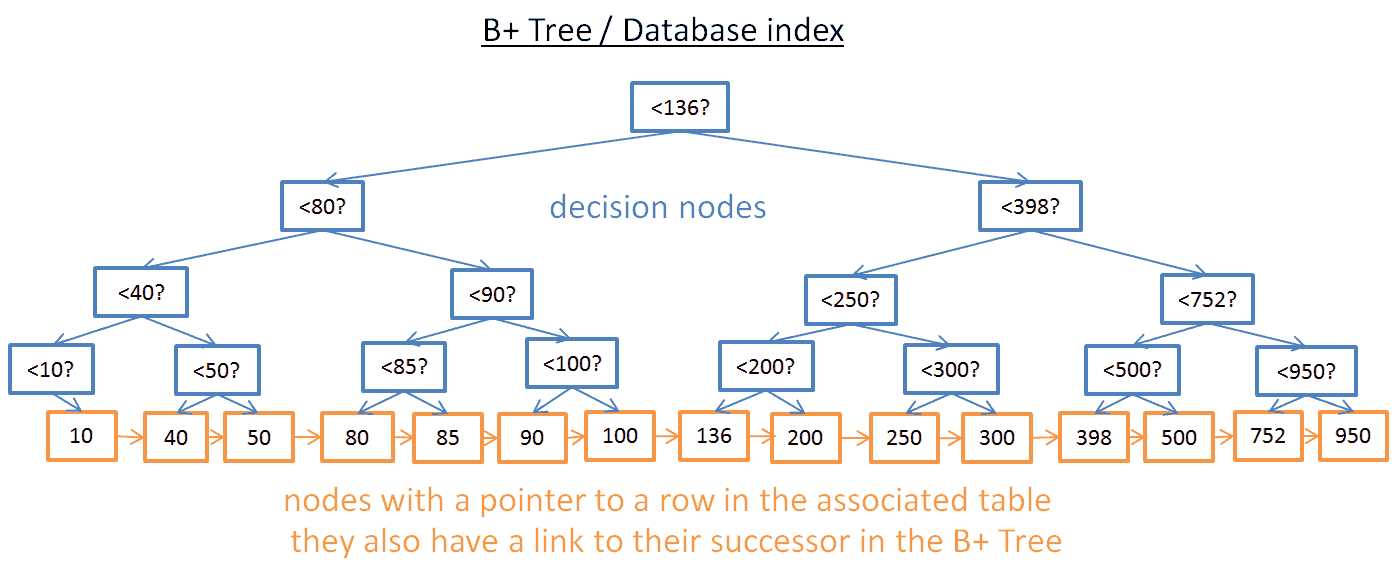
　　可以看到，节点要比之前多（之前的2倍），确实，你增加了“决策节点”用来帮助你找到对的节点（那个存储了数据库表的行所在位置的节点），但查找的时间复杂度依然是O(log(N))（因为只多了一层）。最大的区别是最底层的叶子节点链接起来了。

　　通过B+树，如果你要找40到100之间的值：

　　> 你只要找到40（如果40不存在，那就找大于并最接近40的值）就像在以前的树上查找一样。

　　> 然后你一直通过链接往后找直到100                                                                       假设你找到M个此范围的节点，且树一共有N个节点，找到某个特定的节点需要log(N)次操作。但是，一旦你找到这个节点，你只需要M次操作找到这范围的所有节点。总的查找时间为M+log(N)次操作，之前的树的遍历需要N次操作。你无需读整棵树（只有M+log(N)个节点）节省了磁盘的读写。如果M很小（如200行）且N很大（如10 000 000行），这样效果就体现出来了。

　　但是这样也有新的问题（又来了！）。如果你在数据库中添加或删除一行，那么在其相关的B+树索引中：

　　> 你需要重新保证B+树中节点的顺序

　　> 你需要保证B+树的层次，不然复杂度会从O(log(N)) 变为O(N)  

　　换句话说，这棵B+树需要自排序和自平衡，幸运的是，可以通过巧妙的删除和添加节点来保证，但是这也带来了额外的开销，这些操作的时间复杂度为O(log(N))。这就是为什么你听到太多的索引并不是件好事。确实，这样你让在数据库表中插入/更新/删除一行的操作变得缓慢，因为数据库需要对每个索引花费O(log(N))的时间来更新这些索引。更重要的是添加索引对与事务管理器来说也是个负担（我们将在后面介绍事务管理器）

　　想要了解更多的细节，可以阅读维基百科上的文章B+树，如果你想阅读在数据库中B+树实现的例子，可以阅读来源于一个MySQL核心开发者的文章B+Tree index structure in InnoDB,介绍了MySQL的引擎InnoDB是怎么处理索引的。

哈希表

　　我们最后一个重要的数据结构是哈希表。当你需要查找时非常有用，更重要的是理解哈希表帮助我们理解常用的数据库连接操作hash join，这个数据结构也被数据库用来存储一些内部的东西（如锁表和缓冲池，在后面会做介绍）

　　哈希表可以通过键值快速找到其对应的值，为了构造一个哈希表，你需要定义：

　　> 元素对应的Key值

　　> 哈希函数，它计算储存位置和其Key值之间的对应关系

　　让我们看看一个简单的例子：

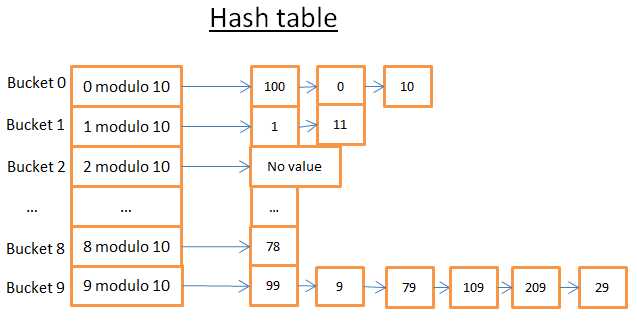
　　这个哈希表一共有是个bucket（桶），我偷懒只画了其中5个，聪明的你肯定可以想象出其他5个。使用的哈希函数是key对10取模，换句话说，我保留整数的最后一为来对应所在bucket编号：

　　> 如果最后一位整数是0，那么它被装在0号桶里

　　> 如果最后一位整数是1，那么它被装载1号桶里

　　> ....　　

　　比如我们要找到元素78：

　　> 哈希函数计算出78对应的桶是8

　　> 去8号桶找，发现第一个元素就是78

　　> 返回78

　　> 整个查找操作只花了2步（第一步计算哈希值，第二步在桶中查找元素）

　　如果我们要找元素59：

　　> 哈希函数计算出59对应9号桶

　　> 去9号桶找，第一个元素是99，不等于59

　　> 往后找9，79...最后找到了29

　　> 元素不存在

　　>整个查找操作花了7步

　　可以看到查找的值不同花费的时间也不同，如果我改变哈希函数为key对1000000取模（取最后的6位数），这时只需要1次操作来找到桶000059。所以哈希表真正的挑战在于找到一个好的哈希函数使桶里装的元素尽量少。有好的哈希函数的，哈希表查找的时间复杂度为O(1)。

　　为什么不使用数组呢？呃，这是一个好问题。

　　> 使用哈希表可以在装载部分到内存，而其他的bucket留在硬盘上。

　　> 数组需要使用连续的内存空间，如果你读入一个超大的表，很难有足够的连续的内存空间。

　　> 使用哈希表你可以选择你想要的作为键值（比如一个城市和姓）

　　想要了解更多，可以读文章Java HashMap，一个哈希表的高效实现方式。你不需要很多Java的知识来理解这篇文章。（未完待续~）

                                                                  译自<how does a relational database work> by Christophe

深入理解关系型数据库(一)

标签：

原文地址：http://www.cnblogs.com/cdefgab1011/p/5687209.html