标签:
BM算法
后缀匹配,是指模式串的比较从右到左,模式串的移动也是从左到右的匹配过程,经典的BM算法其实是对后缀蛮力匹配算法的改进。为了实现更快移动模式串,BM算法定义了两个规则,好后缀规则和坏字符规则,如下图可以清晰的看出他们的含义。利用好后缀和坏字符可以大大加快模式串的移动距离,不是简单的++j,而是j+=max (shift(好后缀), shift(坏字符))
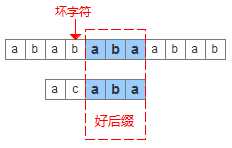
先来看如何根据坏字符来移动模式串,shift(坏字符)分为两种情况:
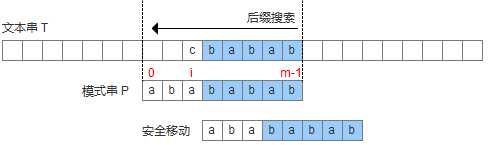
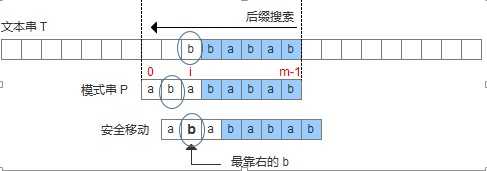
此处配的图是不准确的,因为显然加粗的那个b并不是”最 靠右的”b。而且也与下面给出的代码冲突!我看了论文,论文的意思是最右边的。当然了,尽管一时大意图配错了,论述还是没有问题的,我们可以把图改正一 下,把圈圈中的b改为字母f就好了。接下来的图就不再更改了,大家心里有数就好。
为了用代码来描述上述的两种情况,设计一个数组bmBc[‘k‘],表示坏字符‘k’在模式串中出现的位置距离模式串末尾的最大长度,那么当遇到坏字符的时候,模式串可以移动距离为: shift(坏字符) = bmBc[T[i]]-(m-1-i)。如下图:
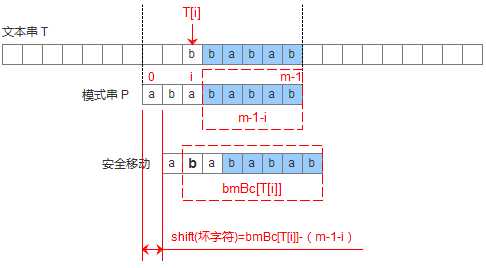
数组bmBc的创建非常简单,直接贴出代码如下:
1 void preBmBc(char *x, int m, int bmBc[]) {
2
3 int i;
4
5 for (i = 0; i < ASIZE; ++i)
6
7 bmBc[i] = m;
8
9 for (i = 0; i < m - 1; ++i)
10
11 bmBc[x[i]] = m - i - 1;
12
13 }
代码分析:
再来看如何根据好后缀规则移动模式串,shift(好后缀)分为三种情况:
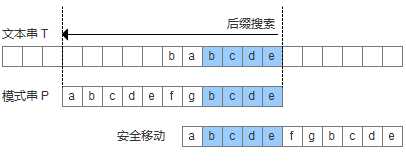
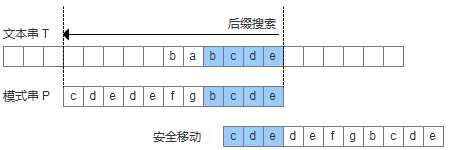
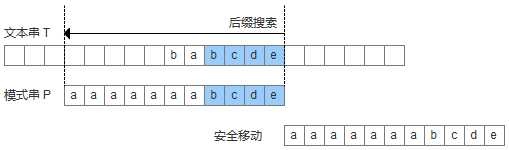
为了实现好后缀规则,需要定义一个数组suffix[],其中suffix[i] = s 表示以i为边界,与模式串后缀匹配的最大长度,如下图所示,用公式可以描述:满足P[i-s, i] == P[m-s, m]的最大长度s。

构建suffix数组的代码如下:
1 void suffixes(char *x, int m, int *suff)
2 {
3 suff[m-1]=m;
4 for (i=m-2;i>=0;--i){
5 q=i;
6 while(q>=0&&x[q]==x[m-1-i+q])
7 --q;
8 suff[i]=i-q;
9 }
10 }
·注解:这一部分代码乏善可陈,都是常规代码,这里就不多说了。
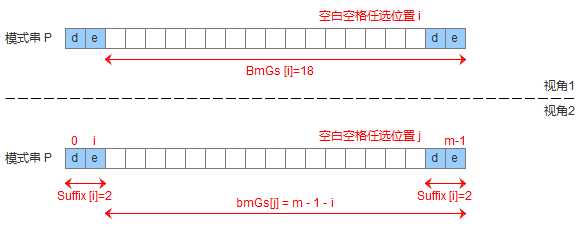
有了suffix数组,就可以定义bmGs[]数组,bmGs[i] 表示遇到好后缀时,模式串应该移动的距离,其中i表示好后缀前面一个字符的位置(也就是坏字符的位置),构建bmGs数组分为三种情况,分别对应上述的移动模式串的三种情况
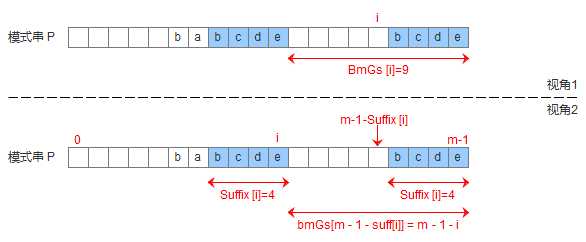

构建bmGs数组的代码如下:
1 void preBmGs(char *x, int m, int bmGs[]) {
2 int i, j, suff[XSIZE];
3 suffixes(x, m, suff);
4 for (i = 0; i < m; ++i)
5 bmGs[i] = m;
6 j = 0;
7 for (i = m - 1; i >= 0; --i)
8 if (suff[i] == i + 1)
9 for (; j < m - 1 - i; ++j)
10 if (bmGs[j] == m)
11 bmGs[j] = m - 1 - i;
12 for (i = 0; i <= m - 2; ++i)
13 bmGs[m - 1 - suff[i]] = m - 1 - i;
14 }
注解:这一部分代码挺有讲究,写的很巧妙,这里谈谈我的理解。讲解代码时候是分为三种情况来说明的,其实第二种和第三种可以合并,因为第三种情况相当于与好后缀匹配的最长前缀长度为0。由于我们的目的是获得精确的bmGs[i],故而若一个 字符同时符合上述三种情况中的几种,那么我们选取最小的bmGs[i]。比如当模式传中既有子串可以匹配上好后串,又有前缀可以匹配好后串的后串,那么此 时我们应该按照前者来移动模式串,也就是bmGs[i]较小的那种情况。故而每次修改bmGs[i]都应该使其变小,记住这一点,很重要!而在这三种情况中第三种情况获得的bmGs[i]值大于第二种大于第一种。故而写代码的时候我们先计算第三种情况,再计算第二种情况,再计算第一种情况。为什么呢,因为对于同一个位置的多次修改只会使得bmGs[i]越来越小。
1. 为什么从后往前,也就是i从大到小?原因在于如果i,j(i>j)位置同时满足第二种情况,那么m-1-i<m-1-j,而第十行代码保证了每个位置最多只能被修改一次,故而应该赋值为m-1-i,这也说明了为什么要从后往前计算。
2. 第8行代码的意思是找到了合适的位置,为什么这么说呢?因为根据suff的定义,我们知道x[i+1-suff[i]…i]==x[m-1-siff[i]…m-1],而suff[i]==i+1,我们知道x[i+1-suff[i]…i]=x[0,i],也就是前缀,满足第二种情况。
3. 第9-11行就是在对满足第二种情况下的赋值了。第十行确保了每个位置最多只能被修改一次。
再来重写一遍BM算法:
1 void BM(char *x, int m, char *y, int n) {
2 int i, j, bmGs[XSIZE], bmBc[ASIZE];
3
4 /* Preprocessing */
5 preBmGs(x, m, bmGs);
6 preBmBc(x, m, bmBc);
7
8 /* Searching */
9 j = 0;
10 while (j <= n - m) {
11 for (i = m - 1; i >= 0 && x[i] == y[i + j]; --i);
12 if (i < 0) {
13 OUTPUT(j);
14 j += bmGs[0];
15 }
16 else
17 j += MAX(bmGs[i], bmBc[y[i + j]] - m + 1 + i);
18 }
19 }
标签:
原文地址:http://www.cnblogs.com/wxgblogs/p/5701101.html