标签:
母串:S[i]
模式串:T[i]
标记数组:Next[i](Next[i]表示T[0~i]最长前缀/后缀数)
先来讲一下最长前缀/后缀的概念
例如有字符串T[6]=abcabd接下来讨论的全部是真前缀/真后缀,也就是除去串自己本身之外的前缀/后缀
T[0]=a,此时前后缀都是a那么Next[0]=1
T[0~1]=ab,此时前缀为a,后缀为b两者不等因此Next[1]=0
T[0~2]=abc,此时前缀为a,ab,后缀为bc,c同上有Next[2]=0
T[0~3]=abca,此时前缀为a,ab,abc,后缀为bca,ca,a可以看到共同部分只有a因此Next[3]=1
T[0~4]=abcab,此时前缀为a,ab,abc,abca,后缀为bcab,cab,ab,b此时最长的公共部分为ab因此Next[4]=2
T[0~5]=abcabd,此时前缀为a,ab,abc,abca,abcab,后缀为bcabd,cabd,abd,bd,d无相等部分故Next[5]=0
说完前后缀的概念之后再来说说KMP的核心思想
例如S=abcabcabdabba,T=abcabd匹配时的情况如下
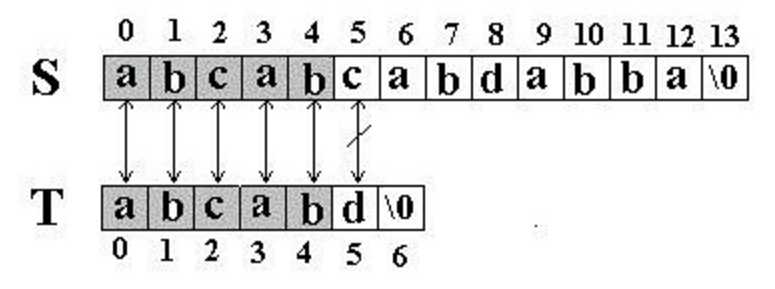
可以看到在S[5]的位置匹配失败,KMP的处理方式如下
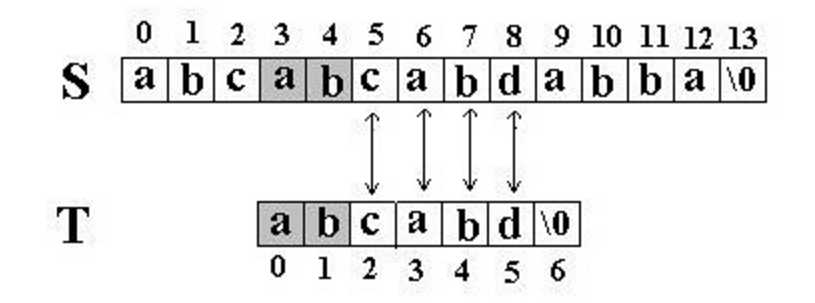
说一下原因,在S[5]的位置匹配失败后直接用S[5]与T[2]去开始匹配,因为Next[5-1]也就是Next[4]=2,因此直接从T[2]重新开始匹配
原因很简单,既然Next[4]=2那么T[0~1]既可以与S[0~1]相等,也可以与S[3~4]相等,所以可以直接从T[2]开始,这也是KMP的精妙所在,不理解的可以自己写两个串试试。所以难点就在于Next数组的实现了,具体实现过程如下
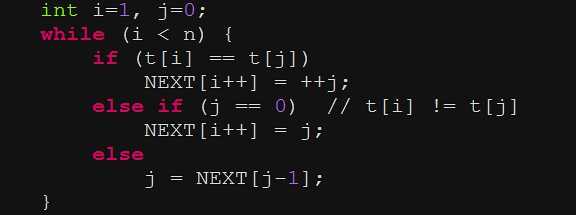
这里只介绍了核心思想,原文比较详细请见:https://www.douban.com/note/321870890/
下面给出kuangbin大神的模板
#include<cstdio> #include<iostream> #include<algorithm> #include<math.h> #include<string.h> #include<vector> #include<queue> #include<iterator> #include<vector> #include<set> #define dinf 0x3f3f3f3f typedef long long ll; //const int Max=(1<<16)+10; using namespace std; #define SIZE 100000005 const int N = 100000005; int m_next[N]; char S[N],T[N]; int slen, tlen; void getNext() { int j, k; j = 0; k = -1; m_next[0] = -1; while(j < tlen) if(k == -1 || T[j] == T[k]) m_next[++j] = ++k; else k = m_next[k]; } /* 返回模式串T在主串S中首次出现的位置 返回的位置是从0开始的。 */ int KMP_Index() { int i = 0, j = 0; getNext(); while(i < slen && j < tlen) { if(j == -1 || S[i] == T[j]) { i++; j++; } else j = m_next[j]; } if(j == tlen) return i - tlen+1; else return -1; } /* 返回模式串在主串S中出现的次数 */ int KMP_Count() { int ans = 0; int i, j = 0; if(slen == 1 && tlen == 1) { if(S[0] == T[0]) return 1; else return 0; } getNext(); for(i = 0; i < slen; i++) { while(j > 0 && S[i] != T[j]) j = m_next[j]; if(S[i] == T[j]) j++; if(j == tlen) { ans++; j = m_next[j]; } } return ans; } int main() { int TT; int i, cc; string str; cin>>TT; while(TT--) { getchar(); scanf("%s %s",&T,&S); slen = strlen(S); tlen = strlen(T); cout<<"模式串T在主串S中首次出现的位置是: "<<KMP_Index()/2+1<<endl; cout<<"模式串T在主串S中出现的次数为: "<<KMP_Count()<<endl; } return 0; }
标签:
原文地址:http://www.cnblogs.com/pter/p/5715034.html