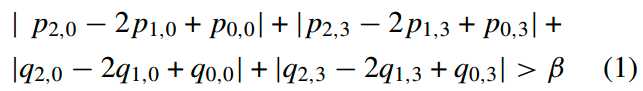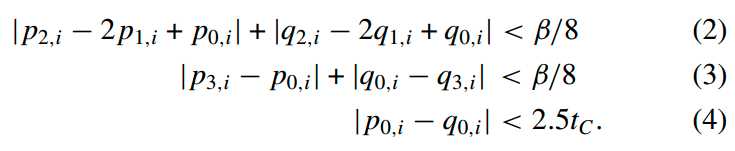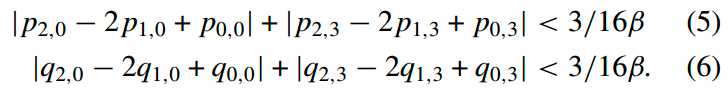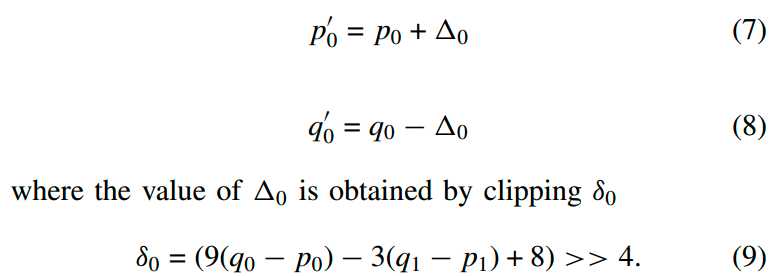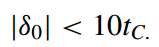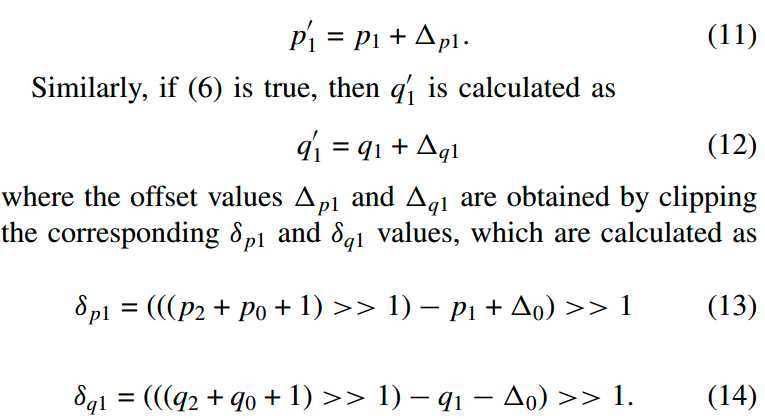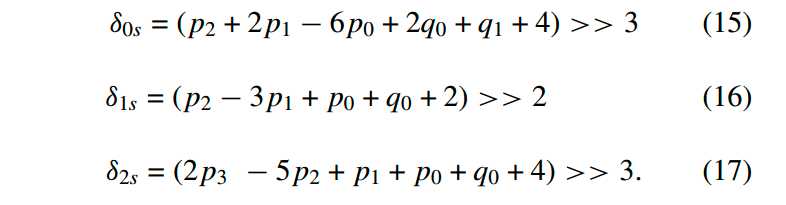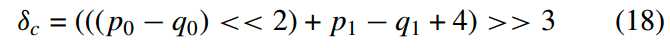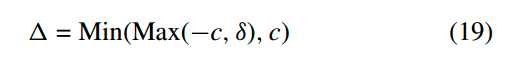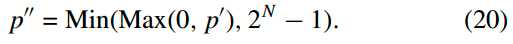标签:
参考论文:HEVC Deblocking Filter
《HEVC标准介绍、HEVC帧间预测论文笔记》系列博客,目录见:http://www.cnblogs.com/DwyaneTalk/p/5711333.html
一、Deblock Filter的目的
在AVC中,图像被分成16x16的MB,对于HEVC则分成16x16到64x64的LCU,LCU按照四叉树结构分成CU,CU的大小从8x8到64x64。CU可以进一步划分成PU和TU,划分成TU也是按照四叉树结构,HEVC支持4x4到32x32的变换大小,更大的变换块也就导致了更加严重的块效应、振铃效应等。
二、Deblock Filter的过程
1、滤波条件判断:DB过程考虑8x8的块边界,对于每个CU,分成8x8的块之后,对于8x8块的每一个边界,进行下面判断决定是否进行DB,以及DB的强度。
A、是否是PU或者TU的边界,如果不是则不进行DB;
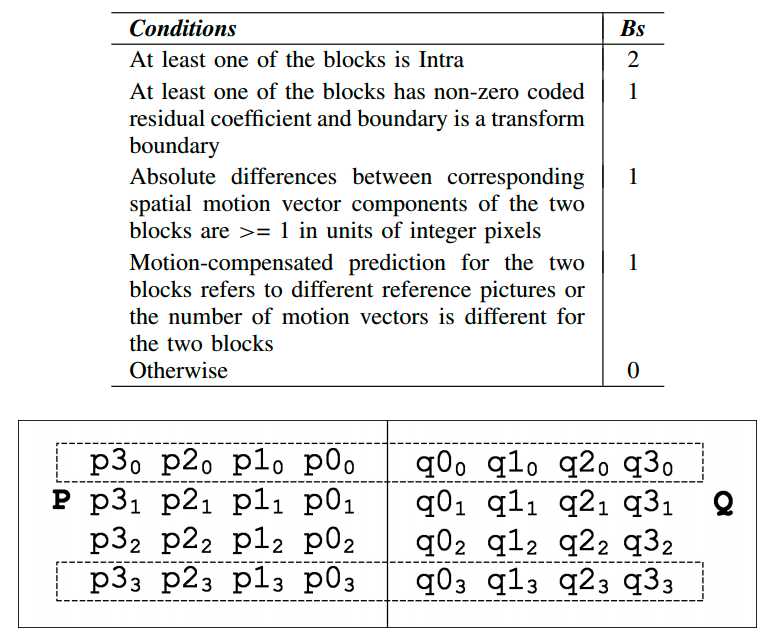
B、进行边界强度BS(boundary strength )的判定,边界强度的确定如下图(对于8x8块的边界,下图中pij和qij是指中间四行、靠近边界的四列,称为four-sample part of a block boundary):

BS = 2:边界两边至少有一个8x8块属于intra,如果满足BS=2的条件,则不进行BS=1的判断;
BS = 1:至少一个8x8块有非0残差系数,且该边界是TU的边界;
BS = 1:两个块的运动矢量的绝对差值大于一个整像素;
BS =1:两个帧间补偿块的参考帧不同或者运动矢量的数目不同;
BS =0:其余情况;
确定BS之后,对于亮度分量:只有当BS>=1时,才会进行DB(需要进一步判断C);对于色度分量,则需要BS=2时,才会进行DB(当A和B满足后,不需要进行C的判断,直接进行滤波)。这表明当边界两遍的块是相对比较平稳的区域时,进行DB的可能性就比较低。对于色度分量,只有边界的两边存在intra块时才会进行DB。
C、局部自适应和滤波判定:就是指当边界两遍的信号变化低于指定的阈值。对于亮度信号,当BS>0时,对于four-sample length boundary,还需要满足下式(只与第1、4行有关)才能进行DB:

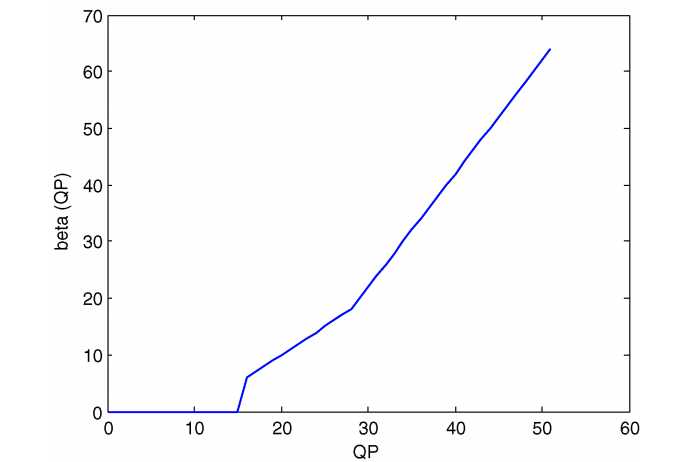
其中belta是与QP有关的,是QP的分段线性函数(具体关系见后面),可以通过查表实现。上式衡量了边界两遍信号值偏离线型的水平(how much signal on both sides of the block boundary deviates from a straight line)。
2、强滤波和普通滤波的判断:对于亮度边界:分为普通滤波和强滤波,其中普通滤波又分为两种情况;而对于色度滤波,则只采用普通滤波的一种情况(只有靠近边界的一个元素进行滤波)。
对于亮度分量,通过下式选择普通滤波还是强滤波,其中i=0、3(表示只对第1和4行进行判断)

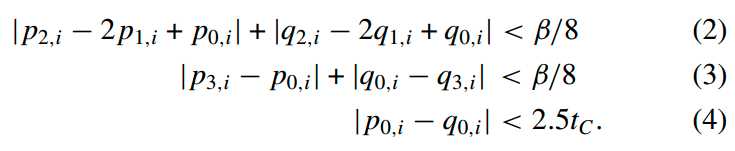
当对于i=0、3时,如果(2)、(3)和(4)式都成立,则进行强滤波,否则进行普通滤波。其中tc也是与QP有关,可以通过查表得到tc的值。条件(2)保证了边缘两边满足更小的局部自适应,条件(3)保证了边缘两边的信号的平稳,条件(4)保证边缘两遍的像素值跳变小于一个阈值。
3、普通滤波的两种情况判定:普通滤波的两种不同情况的区别在于,边界两遍进行滤波的像素的数目不同。判断条件如下:

当条件(5)满足时,边界左边块P中最靠近边界的两个像素位置进行滤波(P1i和P0i,i=0,1,2,3);否则P块中只有最靠近边界的一个像素进行滤波(P0i,i=0,1,2,3)。对于条件(6),情况相同。
这两个条件中,使用的阈值也是和belta有关,但是小于条件(1)中阈值,大于条件(2)、(3)中的阈值,说明对于局部自适应越低的边界,使用越强(或者滤波元素越多)的滤波操作。
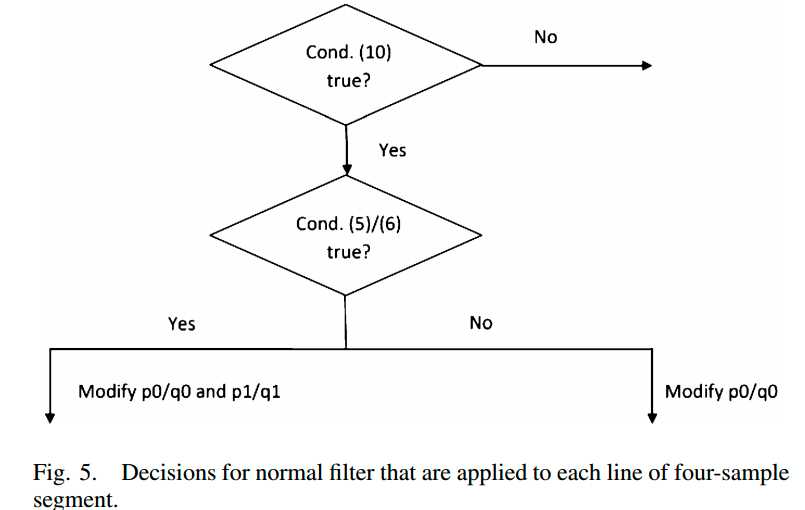
整体滤波条件判断和滤波类型决策过程如下两图:关于条件(10)的说明见后面

4、普通滤波的处理过程:(假设是竖边界)
无论条件(5)和(6)是否满足,都需要对最靠近边界的一列进行滤波,滤波公式如下(行坐标舍去,需要对i=0,1,2,3,共4行都要滤波):

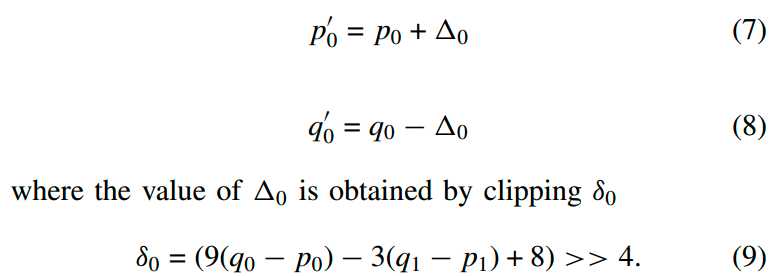
Delta是sita进行clip操作的结果,至于clip操作后面会介绍。上述操作相当于对像素进行了(3,7,9,-3)/16的滤波器进行了滤波。另外,对于i=0,1,2,3的每一行,进行滤波前还需要单独进行条件(10)的判断,只有条件(10)满足了,该行才能够进行滤波:
条件(10)的存在,是为了避免对正常存在的块边界进行不必要的滤波,因为当sita绝对的大于10倍tc时,一般不太可能是由于块效应导致的,所以对于普通滤波的处理过程如下图:
如上图所示:无论正常滤波的那种情况,都需要对p0和q0进行滤波,但是当条件(5)满足时,则需要对p1进行滤波;当条件(6)满足时,需要对q1进行滤波。对p1/q1滤波操作如下:

相当于对p1/q1进行了(8, 19, -1, 9, -3)/32的滤波操作。
5、强滤波的处理过程:(假设竖边界)
对于强滤波,需要影响更多的像素,所以需要对边界两侧每一行的各3个像素进行调整,调整量分别为delta0、delta1和delta2,分别是下面sita0、sita1和sita2的clip操作结果。

也就是说,对于每一行(共4行,i=0,1,2,3)的p0/q0、p1/q1和p2/q2,分别加上/减去delta0、delta1和delta2。这个滤波相当于分别进行了(1, 2, 2, 2, 1)/8、(1, 1, 1, 1)/4和(2, 3, 1, 1, 1)/8的滤波操作。
6、色度的滤波操作:
如上1、2所述,对于色度8x8块边界,是PU或TU边界且BS=2时,不进行其他任何判断,进行对变量两侧每行(i=0,1,2,3)分别一个元素(p0/q0)进行滤波,滤波大小delta是下面sita的clip操作结果,相当于进行了(1 4 4 -1)/8的滤波操作。

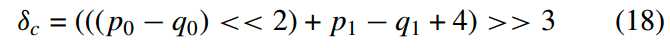
7、Clip操作:
Clip的操作是针对sita进行的,Clip过程如下:

如上式,Clip操作就是将sita的值限定到[-c, c]的区间,其中针对不同的sita,Clip的范围c也不同。对于正常滤波,若delta用于调整p0/q0的值,则c=Tc(n);若delta调整p1/q1,则c=Tc(n)/2。对于强滤波,c=2Tc(n)。对于Tc(n)中的n,当边界两遍都是帧间预测是(BS=0或1),则n=QP;否则n=QP+2;
另外,对于色度分量滤波后的结果p0‘/q0‘,以及亮度分量的正常滤波结果p0‘/q0‘、p1‘/q1‘,需要按照下式进行Clip操作(其中N是bit depth):

8、序列和帧级的DB自适应:
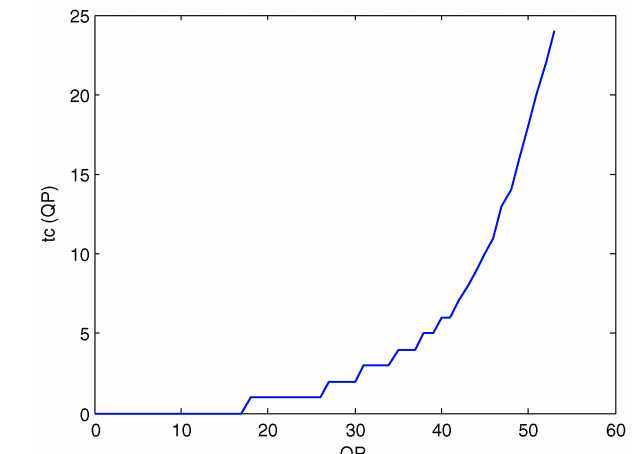
滤波过程中,delta控制哪些边界需要进行滤波,控制在强滤波和正常滤波之间的选择,还控制哪些正常滤波2种情况中的选择。参数Tc除了控制了强滤波和正常滤波的选择之外,还控制滤波补偿量的最大绝对值。二者都是通过QP查表得到,二者与QP的关系如下图:

为了实现序列内不同帧或不同slice的滤波强度的自适应调整,因此在slice header和PPS(picture parameters set)中设置了tc−offset−div2 和beta−offset−div2这两个参数对tc和belta进行调整。在进行tc和belta计算时,相应地把tc−offset−div2 和beta−offset−div2的2倍加到当前的QP上,从而调整tc和belta的值。
【HEVC简介】DB-DeBlock Filter
标签:
原文地址:http://www.cnblogs.com/DwyaneTalk/p/5715053.html