标签:
本节使用的算法称为ID3,另一个决策树构造算法CART以后讲解。
我们经常使用决策树处理分类问题,它的过程类似二十个问题的游戏:参与游戏的一方在脑海里想某个事物,其他参与者向他提出问题,只允许提20个问 题,问题的答案也只能用对或错回答。问问题的人通过推断分解,逐步缩小带猜测事物的范围。
如图1所示的流程图就是一个决策树,长方形代表判断模块(decision block),椭圆形代表终止模块(terminating block),表示已经得出结论,可以终止运行。从判断模块引出的左右箭头称作分支(branch),它可以到达另一个判断模块或终止模块。
图 1构造了一个假象的邮件分类系统,它首先检测发送邮件域名地址。如果地址为myEmployer.com,则将其放在分类"无聊时需要阅读的邮件"中。如 果邮件不是来自这个域名,则检查内容是否包括单词曲棍球,如果包含则将邮件归类到"需要及时处理的朋友邮件",否则将邮件归类到"无须阅读的垃圾邮件"。
- 优点:计算复杂度不高,输出结果易于理解,对中间值的缺失不敏感,可以处理不相关特征数据。
- 缺点:可能会产生过度匹配问题。
- 适用数据类型:离散型和连续型
如果待分类的事务可能划分在多个分类之中,则符号Xi定义为:x
其中p(xi)是选择该分类的概率。
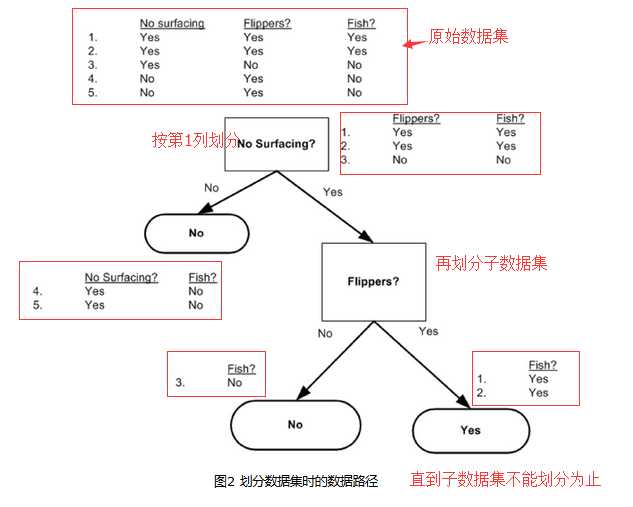
在构造决策树时,我们需要解决的第一个问题就是,当前数据集上哪个特征在划分数据分类时起决定性作用。为了找到决定性的特征,划分出最好的结果,我们必须评估每个特征。我们假设已经根据一定的方法选取了待划分的特征,则原始数据集将根据这个特征被划分为几个数据子集。这数据子集会分布在决策点(关键 特征)的所有分支上。如果某个分支下的数据属于同一类型,则无需进一步对数据集进行分割。如果数据子集内的数据不属于同一类型,则需要递归地重复划分数据 子集的过程,直到每个数据子集内的数据类型相同。如何划分子集的算法和划分原始数据集的方法相同。
创建分支的过程用伪代码表示如下:
检测数据集中的每个子项是否属于同一类型:
If Yes return 类标签
Else
寻找划分数据集的最好特征
划分数据集
创建分支节点
for 每个划分的子集:
递归调用本算法并添加返回结果到分支节点中(这是个递归)
return 分支节点
决策树的一般流程:
- 收集数据:可以使用任何方法。
- 准备数据:树构造算法只适用于标称数据,因此数值型数据必须离散化。
- 分析数据:可以使用任何方法,构造树完成之后,我们应该检查图形是否符合预期。
- 训练算法:构造树的数据结构。
- 测试算法:使用经验树计算错误率。
- 使用算法:此步骤可以适用于任何监督学习算法,而使用决策树可以更好地理解数据的内在含义。
一些决策树算法使用二分法划分数据,本书将使用ID3算法划分数据集,该算法处理如何划分数据集,何时停止划分数据集。每次划分数据集我们只选取一个特征属性,那么应该选择哪个特征作为划分的参考属性呢?
表1的数据包含5个海洋动物,特征包括:不浮出水面是否可以生存,以及是否有脚噗。我们可以将这些动物分成两类:鱼类和非鱼类。
表1 海洋生物数据
| 不浮出水面是否可以生存 | 是否有脚蹼 | 属于鱼类 | |
| 1 | 是 | 是 | 是 |
| 2 | 是 | 是 | 是 |
| 3 | 是 | 否 | 否 |
| 4 | 否 | 是 | 否 |
| 5 | 否 | 是 | 否 |
划分数据集的大原则是:将无序的数据变得更加有序。我们可以使用多种方法划分数据集,但是每种方法都有各自的优缺点。组织杂乱无章数据的一种方法就是使用信息论度量信息,信息论是量化处理信息的分支科学。我们可以在划分数据之前或之后使用信息论量化度量信息的内容。
在划分数据集之前之后信息发生的变化成为信息增益,我们可以计算每个特征划分数据集获得的信息增益,获得信息增益最高的特征就是最好的选择。
集合信息的度量方式成为香农熵或者简称为熵。
为了计算熵,我们需要计算所有类型所有可能值包含的信息的期望值,通过下面的公式得到:
其中n是分类的数目。
下面给出计算信息熵的Python函数,创建名为trees.py文件,添加如下代码:
1 def createDataSet(): 2 dataSet = [[1, 1, ‘yes‘], 3 [1, 1, ‘yes‘], 4 [1, 0, ‘no‘], 5 [0, 1, ‘no‘], 6 [0, 1, ‘no‘]] 7 labels = [‘no surfacing‘,‘flippers‘] 8 #change to discrete values 9 return dataSet, labels 10 def calcShannonEnt(dataSet): 11 numEntries = len(dataSet) #获取数据行数 numEntries = 5 12 labelCounts = {} 13 for featVec in dataSet: #the the number of unique elements and their occurance 14 currentLabel = featVec[-1] 15 if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0 16 labelCounts[currentLabel] += 1 17 shannonEnt = 0.0 18 print("labelCounts=",labelCounts) # labelCounts= {‘yes‘: 2, ‘no‘: 3} 19 for key in labelCounts: 20 prob = float(labelCounts[key])/numEntries # prob 为每个值出现的概率 21 shannonEnt -= prob * log(prob,2) # 数学公式,计算 熵 22 print("shannonEnt=",shannonEnt) 23 return shannonEnt
测试代码:
1 >>> d,l=trees.createDataSet() 2 >>> d 3 [[1, 1, ‘yes‘], [1, 1, ‘yes‘], [1, 0, ‘no‘], [0, 1, ‘no‘], [0, 1, ‘no‘]] 4 >>> l 5 [‘no surfacing‘, ‘flippers‘] 6 >>> c=trees.calcShannonEnt(d) 7 labelCounts= {‘yes‘: 2, ‘no‘: 3} 8 shannonEnt= 0.9709505944546686 9 >>>
calcShannonEnt:返回整个数据集的 熵
上面测试代码数据集的熵=0.9709505944546686
熵 值越高,则混合的数据也越多,得到 熵 之后,我们就可以按最大信息增益的方法划分数据集。
上面我们学习了如何度量数据集的无序程序,分类算法除了需要测量信息熵,还需要划分数据集,度量划分数据集的熵,以便判断当前是否正确地划分了数据集。
我们将对每个特征划分数据集的结果计算一次信息熵,然后判断按照哪个特征划分数据集市最好的划分方法。
按照给定的特征划分数据集:
1 def splitDataSet(dataSet, axis, value):#查找数据集 dataSet 第 axis 列值== value 的元素,再排除第 axis 列的数据,组成一个新的数据集 2 retDataSet = [] 3 for featVec in dataSet: 4 if featVec[axis] == value: 5 reducedFeatVec = featVec[:axis] #chop out axis used for splitting 6 reducedFeatVec.extend(featVec[axis+1:]) 7 retDataSet.append(reducedFeatVec) 8 return retDataSet
该函数使用了三个输入参数:带划分的数据集、划分数据集的特征(数据集第几列)、需要返回的特征的值(按哪个值划分)。函数先选取数据集中第axis个特征值为value的数据,从这部分数据中去除第axis个特征,并返回。
测试这个函数,效果如下:
1 >>> myDat, labels = trees.createDataSet() 2 >>> myDat 3 [[1, 1, ‘yes‘], [1, 1, ‘yes‘], [1, 0, ‘no‘], [0, 1, ‘no‘], [0, 1, ‘no‘]] 4 >>> trees.splitDataSet(myDat, 0, 1) #查找第0列值==1的元素,再排除第0列的数据,组成一个新的数据集 5 [[1, ‘yes‘], [1, ‘yes‘], [0, ‘no‘]] 6 >>> trees.splitDataSet(myDat, 0, 0) 7 [[1, ‘no‘], [1, ‘no‘]]
接下来我们将遍历整个数据集,循环计算香农熵和splitDataSet()函数,找到最好的特征划分方式。熵计算将会告诉我们如何划分数据集是最好的数据组织方式。
选择最好的数据集划分方式:
1 def chooseBestFeatureToSplit(dataSet): 2 numFeatures = len(dataSet[0]) - 1 # 这里的dataSet 最后一列是分类 numFeatures=2;我们按2列数据进行划分 3 baseEntropy = calcShannonEnt(dataSet) # 计算出整个 数据数据集的 熵 4 bestInfoGain = 0.0; bestFeature = -1 5 for i in range(numFeatures): # 循环每一列特征 6 featList = [example[i] for example in dataSet]# 创建一个新的 列表,存放数据集第 i 列的数据 7 uniqueVals = set(featList) # 使用集合,把数据去重。。。。。。。。。。 8 newEntropy = 0.0 # 以下是计算 每一列 的 熵 求某列 最大的 熵 9 for value in uniqueVals:# 循环 第 i 列 的特征值 10 subDataSet = splitDataSet(dataSet, i, value) # 划分数据集。。。。 11 prob = len(subDataSet)/float(len(dataSet)) # 子数据集所占的比例。。。。 12 newEntropy += prob * calcShannonEnt(subDataSet) # 子数据集的 熵 * 比例。。。。 13 infoGain = baseEntropy - newEntropy #calculate the info gain; ie reduction in entropy 14 if (infoGain > bestInfoGain): #compare this to the best gain so far 15 bestInfoGain = infoGain #if better than current best, set to best 16 bestFeature = i 17 return bestFeature #returns an integer 返回按某列划分数据集的最大 熵
- 本函数使用变量bestInfoGain和bestFeature记录最好的信息增益和对应的特征;
- numFeatures记录特征维数,依次遍历各个特征,计算该特征值的集合(uniqueVals);
- 遍历该特征计算使用该特征划分的熵(newEntropy),据此计算新的信息增益(infoGain);
- 比较infoGain和bestInfoGain记录信息增益的最大值和对应特征;
- 最终返回最大的信息增益对应特征的索引。
测试上面代码的实际输出结果:
1 >>> myData, labels = trees.createDataSet() 2 >>> trees.chooseBestFeatureToSplit(myData) 3 labelCounts= {‘yes‘: 2, ‘no‘: 3} 4 shannonEnt= 0.9709505944546686 5 labelCounts= {‘no‘: 2} 6 shannonEnt= 0.0 7 labelCounts= {‘yes‘: 2, ‘no‘: 1} 8 shannonEnt= 0.9182958340544896 9 labelCounts= {‘no‘: 1} 10 shannonEnt= 0.0 11 labelCounts= {‘yes‘: 2, ‘no‘: 2} 12 shannonEnt= 1.0 13 0
构建决策树的算法流程如下:
- 得到原始数据集,
- 基于最好的属性值划分数据集,由于特征值可能多于两个,因此可能存在大于两个分支的数据集划分。
- 第一次划分之后,数据将被向下传递到树分支的下一个节点,在这个节点上,我们可以再次划分数据。我们可以采用递归的原则处理数据集。
- 递归结束的条件是,程序遍历完所有划分数据集的属性,或者每个分支下的所有实例都具有相同的分类。
添加下面的程序代码:
1 def majorityCnt(classList):# 返回 出现次数最多的类别 ,,类似于K-近邻算法中 返回前K中类别出现最多次数的。 2 classCount={} 3 for vote in classList: 4 if vote not in classCount.keys(): classCount[vote] = 0 5 classCount[vote] += 1 6 sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True) 7 return sortedClassCount[0][0] 8 9 def createTree(dataSet,labels): 10 classList = [example[-1] for example in dataSet] # 获取数据集的所有类别 11 if classList.count(classList[0]) == len(classList): 12 return classList[0]# 如果数据集的所有类别 都相同,则不需要划分 13 if len(dataSet[0]) == 1: # 使用完了所有特征,仍然不能将数据划分 到某个类别上的话,返回出现次数最多的类别 14 return majorityCnt(classList) 15 bestFeat = chooseBestFeatureToSplit(dataSet) # 获取数据集中 按哪一列进行划分。。。。。 16 bestFeatLabel = labels[bestFeat] # bestFeatLabel = 列 描述 17 myTree = {bestFeatLabel:{}} # 创建一个字典 18 del(labels[bestFeat]) # 删除已计算过的列 19 featValues = [example[bestFeat] for example in dataSet] 20 uniqueVals = set(featValues) # 获取某列 所有不重复值 21 for value in uniqueVals: 22 subLabels = labels[:] #copy all of labels, so trees don‘t mess up existing labels 23 myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels) # 递归 24 return myTree 25
majorityCnt函数统计classList列表中每个类型标签出现频率,返回出现次数最多的分类名称。
createTree函数使用两个输入参数:数据集dataSet和标签列表labels。标签列表包含了数据集中所有特征的标签,算法本身并不需 要这个变量,但是为了给出数据明确的含义,我们将它作为一个输入参数提供。上述代码首先创建了名为classList的列表变量,其中包含了数据集的所有 类标签。列表变量classList包含了数据集的所有类标签。递归函数的第一个停止条件是所有类标签完全相同,则直接返回该类标签。递归函数的第二个停 止条件是使用完了所有特征,仍然不能将数据集划分成仅包含唯一类别的分组。这里使用majorityCnt函数挑选出现次数最多的类别作为返回值。
下一步程序开始创建树,这里直接使用Python的字典类型存储树的信息。字典变量myTree存储树的所有信息。当前数据集选取的最好特征存储在变量bestFeat中,得到列表中包含的所有属性值。
最后代码遍历当前选择特征包含的所有属性值,在每个数据集划分上递归待用函数createTree(),得到的返回值将被插入到字典变量myTree中,因此函数终止执行时,字典中将会嵌套很多代表叶子节点信息的字典数据。
注意其中的subLabels = labels[:]复制了类标签,因为在递归调用createTree函数中会改变标签列表的值。
测试这些函数:
1 >>> myDat, labels = trees.createDataSet() 2 >>> myTree = trees.createTree(myDat, labels) 3 >>> myTree 4 {‘no surfacing‘: {0: ‘no‘, 1: {‘flippers‘: {0: ‘no‘, 1: ‘yes‘}}}}
变量myTree包含了很多代表树结构信息的嵌套字典,从左边开始,第一个关键字no surfacing 是第一个划分数据集特征的名称,该关键字的值也是一个字典。
依靠训练数据构造了决策树之后,我们可以将它用于实际数据的分类。在执行数据分类时,需要决策树以及用于决策树的标签向量。然后,程序比较测试数据与决策树上的数值,递归执行该过程直到进入叶子结点;最后将测试数据定义为叶子结点所属的类型。
使用决策树分类的函数:
1 def classify(inputTree,featLabels,testVec): 2 firstStr = inputTree.keys()[0] 3 secondDict = inputTree[firstStr] 4 featIndex = featLabels.index(firstStr) 5 key = testVec[featIndex] 6 valueOfFeat = secondDict[key] 7 if isinstance(valueOfFeat, dict): 8 classLabel = classify(valueOfFeat, featLabels, testVec) 9 else: classLabel = valueOfFeat 10 return classLabel
测试上面的分类函数:
>>> myDat, labels = trees.createDataSet() >>> myTree = trees.createTree(myDat, labels[:]) >>> trees.classify(myTree, labels, [1, 0]) ‘no‘ >>> trees.classify(myTree, labels, [1, 1]) ‘yes‘
可以使用Python模块pickle序列化对象,参见下面的程序。序列化对象可以在磁盘上保存对象,并在需要的时候读取出来。
1 def storeTree(inputTree, filename): 2 import pickle 3 fw = open(filename, ‘w‘) 4 pickle.dump(inputTree, fw) 5 fw.close() 6 7 def grabTree(filename): 8 import pickle 9 fr = open(filename) 10 return pickle.load(fr)
>>> fr = open(‘lenses.txt‘) >>> lensens = [inst.strip().split(‘\t‘) for inst in fr.readlines()] >>> lensensLabels = [‘age‘, ‘prescript‘, ‘astigmatic‘, ‘tearRate‘] >>> lensesTree = trees.createTree(lensens,lensensLabels) >>> lensensTree
执行结果:{‘tearRate‘: {‘normal‘: {‘astigmatic‘: {‘yes‘: {‘prescript‘: {‘hyper‘: {‘age‘: {‘pre‘: ‘no lenses‘, ‘presbyopic‘: ‘no lenses‘, ‘young‘: ‘hard‘}}, ‘myope‘: ‘hard‘}}, ‘no‘: {‘age‘: {‘pre‘: ‘soft‘, ‘presbyopic‘: {‘prescript‘: {‘hyper‘: ‘soft‘, ‘myope‘: ‘no lenses‘}}, ‘young‘: ‘soft‘}}}}, ‘reduced‘: ‘no lenses‘}}
- 计算整个数据集的 熵
- 根据第1处计算出来的熵 再计算数据集按哪一列划分最为合适(计算数据集每一列的 熵 ,根据所有列计算出来的 熵 获取最佳列),设此处计算出最佳列为 I
- 获取数据集第 I 列所有不重复值的集合,设此处集合为 M
- for v in M 循环集合 M
- 根据 I 列 和 v 值 划分数据集
- 再递归运算
标签:
原文地址:http://www.cnblogs.com/netuml/p/5724750.html