machine-learning课程学习总结（1-4）

标签：

一、绪论 

    1.概念：

• the field of study that gives computers the ability to learn without being explicitly programmed. ——an older, informal definition by  Arthur Samuel （对于无法直接编程的任务让 机器 通过学习来实现）
•  "A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.（机器做任务T时通过实践E来提升自己的表现P）

   2.机器学习问题分为两大类：监督式学习（supervised learning）和非监督式学习（unsupervised learning）

• supervised learning: we are given a data set and already know what our correct output should look like, having the idea that there is a relationship between the input and the output.（对于输入数据，明确知道输出数据应该是什么）。监督式学习又分为回归（regression）和归类（classification）问题。回归问题是将输入数据映射到一个连续的函数（对应输出数据）上面，然后来预测结果。归类问题是将输入数据映射到离散的类别里面（对应输出数据），然后根据离散的输出值预测结果。
• unsupervised learning:  allows us to approach problems with little or no idea what our results should look like. We can derive structure from data where we don‘t necessarily know the effect of the variables.（不知结果是什么，但可以试着从中找到数据的某些联系，对于预测的结果，我们也无法判断是对是错）。     

　　  非监督式学习的例子：

　　   Clustering: Take a collection of 1000 essays written on the US Economy, and find a way to automatically group these essays into a        small number that are somehow similar or related by different variables, such as word frequency, sentence length, page count, and so on.

　　   Non-clustering: The "Cocktail Party Algorithm", which can find structure in messy data (such as the identification of individual voices and  music from a mesh of sounds at a cocktail party). 

二、单变量的线性回归（univariate linear regression）

  1.概念：predict a single output value y from a single input value x.（以一个变量x来预测y）

  2.假说函数：用一个函数来估计输出值，这里用h(x)去估计y，函数如下：

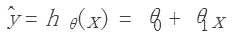
  3.代价函数：用来评估假说函数是否准确，类似方差（Squared error function/ Mean squared error），函数如下：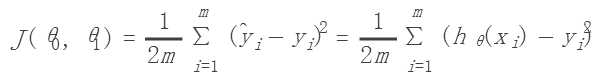

三、梯度下降（gradient descent）

1. 概念：a way to automatically improve the parameters of our hypothesis function

    简而言之，梯度下降就是求最合适的那些参数。分别以θ0,θ1为x,y轴，画出代价函数J，我们要使得代价函数最小，就是找该函数J的最小值。可以通过J 对θ0，θ1分别求偏导来找出极值点，从而找到最小值。

    梯度下降算法如下：

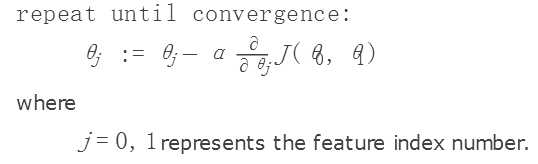
2.将其应用于我们上面的线性回归，那么就是：

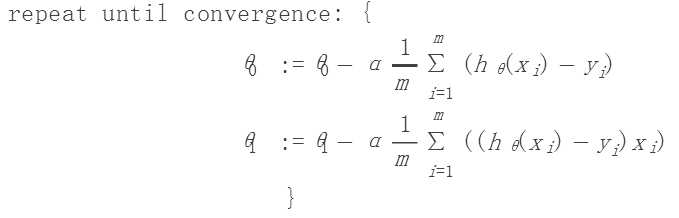
四、多变量的线性回归（multivariate linear regression）

1.和单变量的差不多，只是多了参数。下面我们先定义一些标号：

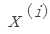：第i 个训练样本，包含一系列特征值，是一个列向量。

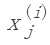：第i 个训练样本中第j 个特征值。

θ：参数θ0，θ1...的一个列向量。（n*1）

m:训练样本个数。

n:特征值个数。

那么我们的训练样本X就是：

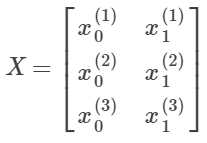（m*n）

2.假说函数：

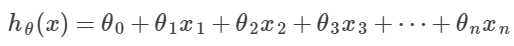
 用矩阵来写，就是：

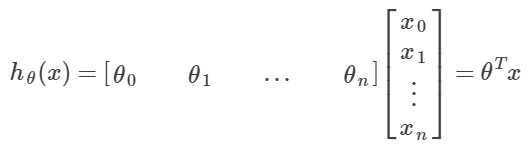
用我们上面定义的标号来写就是：

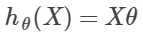
3.代价函数：

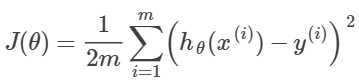
用矩阵来写就是：

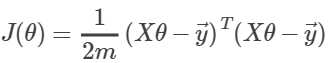（其中y^→为所有y值得一个列向量）

4.梯度下降：

求偏导带入公式，得：

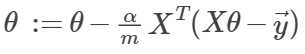
5.特征正规化（feature nomalization）：

将输入值调整在一个相同的范围内可以加速梯度下降的过程，理想情况下，将每个输入值都调整在[-0.5，0.5],[-1,1]之间。

方法：

 feature scaling （/s）和mean normalization（-μ），统计学中的：

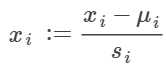（μ为特征数均值，s为标准差）

6.多项式回归（polynomial regression）:

  线性回归可能不能很好拟合数据，这时候在假说函数中加入平方，立方，开方项来更好拟合数据

For example, if our hypothesis function is hθ(x)=θ0+θ1x then we can create additional features based on x, to get the quadratic function hθ(x)=θ0+θ1x+θ2x^2 or the cubic function hθ(x)=θ0+θ1x+θ2x^2+θ3x^3

7.normal equation:

  不迭代直接求最佳的参数，直接解出θ：（让偏导为0，用逆矩阵解）

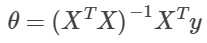
其中，X‘X有时是不可逆的，不可逆的情况有：特征值冗余，比如可能两个之间成比例，可以去掉一个；太多 features(m<=n),可以去掉一些

两种方法的比较：

machine-learning课程学习总结（1-4）

标签：

原文地址：http://www.cnblogs.com/cherry-yue/p/5726533.html