标签:
一、数据结构背景+代码变量介绍
二叉查找树,又名二叉排序树,亦名二叉搜索树
它满足以下定义:
1、任意节点的子树又是一颗二叉查找树,且左子树的每个节点均小于该节点,右子树的每个节点均大于该节点。
2、由1可推出,任意节点的左孩子小于该节点,右孩子大于该节点
以上讨论的是左(右)孩子(子树)存在的情况
它的中序遍历是一个升序的排序
在参考代码中,我们定义有:
主程序中,k代表插入或删除或查找的节点的值
root,根节点位置;a[i],第 i 号节点的值;cl[i],第 i 号节点左孩子的位置;cr[i],第 i 号节点右孩子的位置;fa[i],父亲节点位置;
二、中序遍历
中序遍历的求法采用递归,先递归它的左孩子,然后打印当前节点,最后递归它的右孩子(当左或右孩子存在时才进行递归)
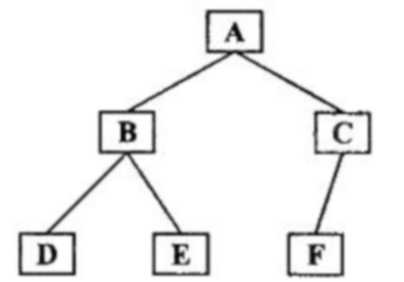
如上图的中序遍历为 DBEAFC
时间复杂度O(n)
1 void mid(int x)
2 {
3 if (time[cl[x]]!=0) mid(cl[x]);
4 cout<<a[x]<<" ";
5 if (time[cr[x]]!=0) mid(cr[x]);
6 }
7
8 主程序中:mid(root);
三、插入节点
我们采用遇到相同的节点,使该节点计数器+1的办法
先从根节点出发:
1、若当前节点小于插入的数,则递归进入其左儿子
若左儿子计数器为0,即不存在左儿子,则直接将数插入到左儿子
2、若当前节点大于插入的数,则递归进入其右儿子
若右儿子计数器为0,即不存在右儿子,则直接将数插入到右儿子
3、若当前节点等于插入的数,则直接将该节点计数器+1
样例一
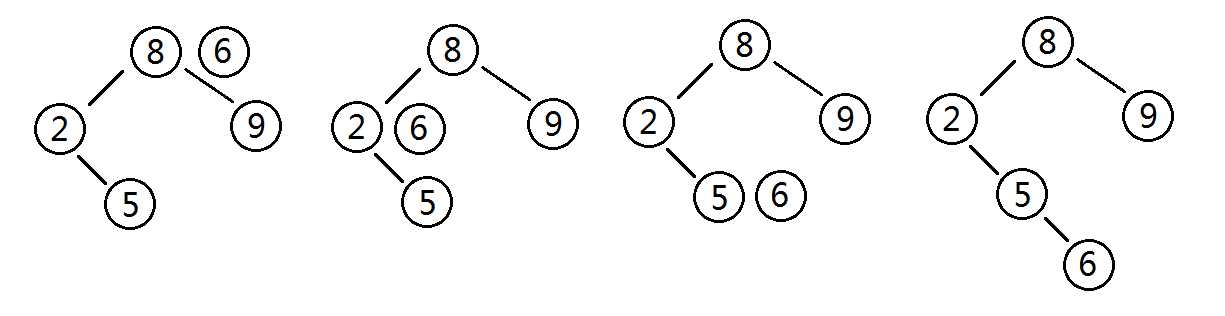
如上图,将6插入该二叉树
1、与根节点比较,小于根节点,进入左儿子
2、与2比较,大于2,进入右儿子
3、与5比较,大于5,进入右儿子,但因右儿子不存在,所以将6作为其右儿子
样例二
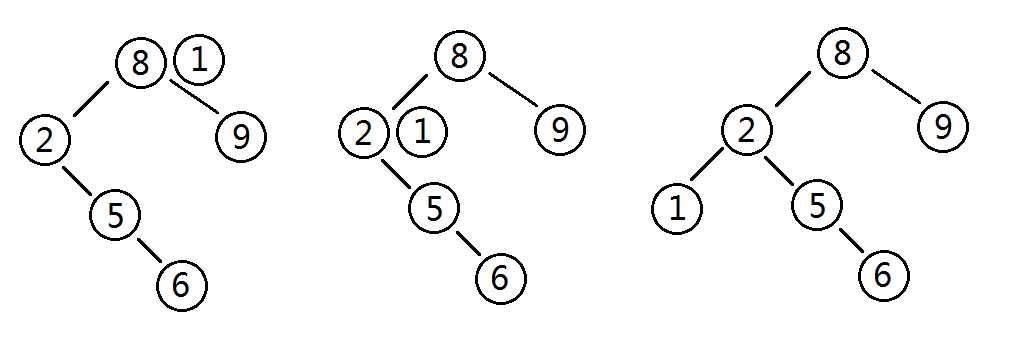
如上图,将1插入该二叉树:
1、与根节点比较,小于8,进入左儿子
2、与2比较,小于2,进入左儿子,但因其左儿子不存在,所以将1作为其左儿子
时间复杂度O(log2n)
1 void ins(int i,int x)
2 {
3 if (root==0)
4 {
5 a[1]=x;
6 time[1]=root=1;
7 return;
8 }
9 if (x<a[i])
10 {
11 if (time[cl[i]]==0)
12 {
13 cl[i]=top>0?s[top--]:++tail;14 a[cl[i]]=x;
15 fa[cl[i]]=i;
16 time[cl[i]]++;
17 cr[cl[i]]=cl[cl[i]]=0;
18 }
19 else ins(cl[i],x);
20 }
21 else if (x>a[i])
22 {
23 if (time[cr[i]]==0)
24 {
25 cr[i]=top>0?s[top--]:++tail;26 a[cr[i]]=x;
27 fa[cr[i]]=i;
28 time[cr[i]]++;
29 cr[cr[i]]=cl[cr[i]]=0;
30 }
31 else ins(cr[i],x);
32 }
33 else
34 {
35 time[i]++;
36 }
37 }
38
39 主程序中:ser(root,k); root代表起始位置,k代表插入的值
四、查找节点
查找类似于插入
同样从根节点出发,如果遇到了空节点,即计数器等于0的节点,直接返回0,表示未查找到
若该节点等于查找的值,则返回该节点的位置
若该节点大于查找的值,则向左儿子递归查找
若该节点小于查找的值,则向右儿子递归查找
此处说明,若当前节点为空节点,则说明小于(大于)该节点父亲的值不存在,即未查找到
查找类似于线段树思想,是一步步向下把范围缩小,直到找到期望的值或无结果
样例一
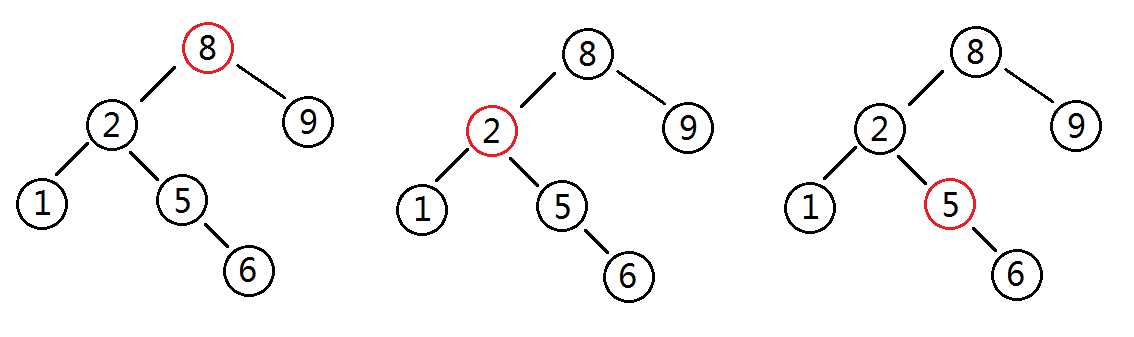
如上图,需查找的值为5
1、查找根节点,5<8,进入左儿子
2、5>2,进入右儿子
3、5=5,查找到该节点,返回该节点的位置
若需查找的值为4时,在第3步会进入其左儿子,又因左儿子为空节点,则返回0,说明未查找到
时间复杂度O(log2n)
1 int sea(int i,int x)
2 {
3 if (time[i]==0) return 0;
4 if (a[i]==x) return i;
5 else if (a[i]>x) return ser(cl[i],x);
6 else return ser(cr[i],x);
7 }
8
9 主程序中:sea(root,k); root代表查找的起始位置,k代表查找的值
五、删除节点
当需要删除节点时,先查找改值所在的位置,然后再进行删除
如果该节点计数器大于1,则只用把计数器-1
如果计数器等于1,即删除后该节点不再存在,则根据儿子的数目分为三种情况:
1、没有儿子:直接将该节点删除
2、一个儿子:将该节点父亲的左(右)儿子直接指向该节点的唯一的那个儿子
3、两个儿子:在该节点的右子树中寻找一个最小的值,然后用最小的那个节点替代该节点,最后删除最小的节点
寻找最小节点具体方法:先将目前节点指向右儿子,然后寻找不断指向目前节点的左儿子,直到没有左儿子为止
因为需要删除的最小节点肯定没有左儿子,所以只需递归执行第1或第2种情况,即 del(最小节点位置,最小节点的值)具体请参考代码
样例一
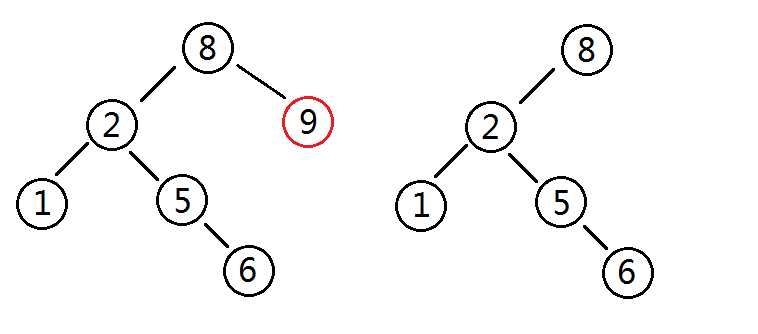
删除9节点:调用查找,查找到9的位置,因为它没有儿子,可直接删除
样例二
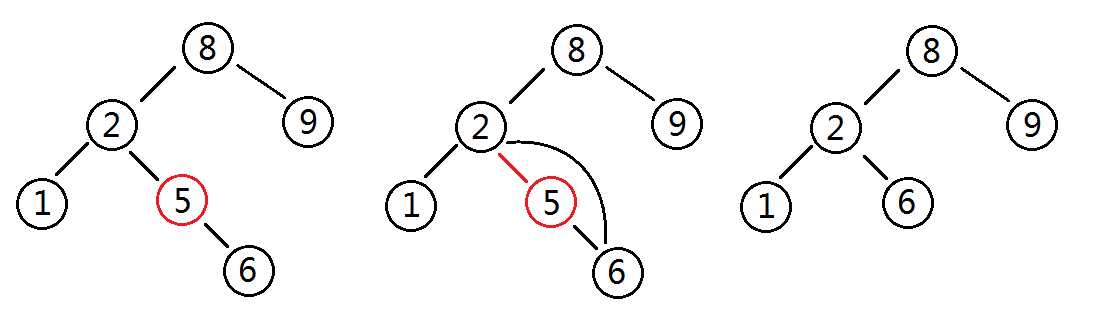
删除5节点:同样查找5节点的位置,发现其有1个孩子,则将 5节点 的 父亲2节点 的 右孩子 指向 5节点 的 孩子6节点,这样就自动删除了5节点
样例三
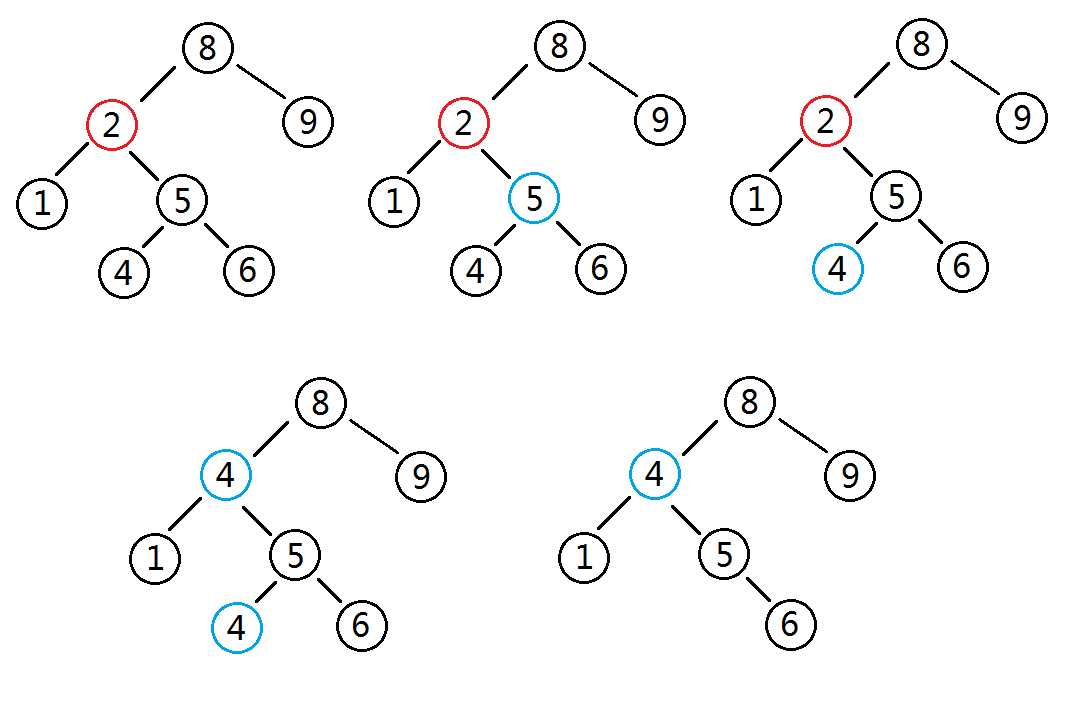
删除2节点:
1、查找到2节点的位置
2、把最小节点指向其右孩子
3、不断寻找目前最小节点的左孩子,直到尽头,找到最小节点
4、将最小节点的信息赋给2节点
5、按照删除节点的方法删除最小节点4节点
时间复杂度O(log2n)
1 void del(int k,int x)
2 {
3 int ct=0;
4 if (cl[k]!=0) ct++;
5 if (cr[k]!=0) ct++;
6 time[k]--;
7 if (time[k]==0)
8 {
9 if (ct==1)
10 {
11 s[++top]=k;12 if (k==root)
13 {
14 root=time[cr[k]]==0?cl[k]:cr[k];
15 return;
16 }
17 if (x<a[fa[k]]) cl[fa[k]]=time[cr[k]]==0?cl[k]:cr[k];
18 else cr[fa[k]]=time[cr[k]]==0?cl[k]:cr[k];
19 }
20 else if (ct==2)
21 {
22 int s=cr[k];
23 if (time[cl[s]]!=0) s=cl[s];
24 time[k]=time[s];
25 a[k]=a[s];
26 del(s,a[s]);
27 }
28 else s[++top]=k;29 }
30 }
31
32 主程序中:del(sea(root,k),k); 先查找到需删除的节点的位置,然后删除k
六、空节点位置栈
在删除节点的时候,会产生许多空节点
为了节省空间,我们会开一个栈来保存空节点的位置,当删除某个节点后,把它空出来的位置压入栈中
当插入节点时,先询问栈顶top是否大于0,若栈中有元素,则把栈中的位置弹出,用该位置存放节点
若栈中没有元素,表示前面没有空的位置,则新开一个空间来存放节点,通过保存最大位置数的变量tail来控制最大位置
七、特殊情况
对于二叉查找树会产生如下图的情况
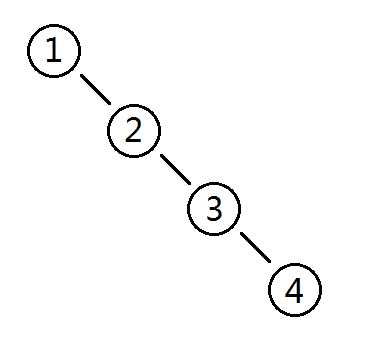
则所有操作的时间往往会被卡成线性O(n),而利用平衡二叉树、伸展树、红黑树等等数据结构便会帮我们解决这个问题
标签:
原文地址:http://www.cnblogs.com/Leo_wl/p/5727623.html