标签:
首先我们先介绍一下普通的插排,就是我们现在一般写的那种,效率是O(n^2)的。
普通的插排基于的思想就是找位置,然后插入进去,其他在它后面的元素全部后移,下面是普通插排的代码:
1 #include<iostream> 2 #include<fstream> 3 #include<stdio.h> 4 using namespace std; 5 int a[200000]; 6 int p[200000]; 7 8 int main(){ 9 ios::sync_with_stdio(false); 10 int n; 11 cin>>n; 12 for(int i=1;i<=n;i++){ 13 cin>>a[i]; 14 } 15 int len = 1; 16 p[len] = a[1]; 17 for(int i=2;i<=n;i++){ //插入第i个元素 18 int k = a[i]; 19 int j; 20 for(j=len;j>=1;j--){ 21 if(k < p[j]){ 22 p[j+1] = p[j]; 23 }else 24 break; 25 } 26 p[j+1] = k; 27 len++; 28 } 29 for(int i=1;i<=n;i++) 30 cout<<p[i]<<" "; 31 return 0; 32 }
可以看出,这个代码的复杂度应该是T((1+n)*n/2)=O(n^2)的,让我们仔细分析到底时间费在哪里。
1.查找过程太费时间,仔细观察我们就可以发现,查找它应当插入元素的位置的时间是O(n)的,我们可以想办法优化成O(log2n),没错,二分查找,于是我们写出了下面这份代码。
1 #include<iostream> 2 #include<cstdio> 3 #include<cstdlib> 4 #include<vector> 5 #include<algorithm> 6 using namespace std; 7 int a[200000]; 8 vector <int> vec; 9 10 int main(){ 11 ios::sync_with_stdio(false); 12 int n; 13 cin >> n; 14 for(int i =1;i<=n;i++) 15 cin>>a[i]; 16 vec.push_back(a[1]); 17 for(int i=2;i<=n;i++){ 18 int k=a[i]; 19 int j=lower_bound(vec.begin(),vec.end(),k)-vec.begin(); 20 vec.insert(vec.begin()+j,k); //这是O(n)的 21 } 22 for(int i=0;i<n;i++){ 23 cout<<vec[i]<<" "; 24 } 25 return 0; 26 }
显然,这份代码的复杂度,应该是T(n*(log2n+n))=O(n^2)的,但是有一点好的,就是不会被某些专门卡插排的数据卡。
我们再分析一下另一个耗时间的地方。
2.将所有元素前移的时间的上界是O(n)的,我们也要想办法优化到O(logn)。若我们只针对这一点优化,那么我们可以想到一种比O(logn)更快的数据结构来优化这一点,链表。
如果我们用链表来储存,我们完全没必要将元素前移,只要连接起来,是O(1)的。不难写出下面这份代码
1 #include<iostream> 2 #include<cstdio> 3 #include<cstdlib> 4 #include<cstring> 5 using namespace std; 6 struct node{ 7 int data; 8 node* next; 9 }; 10 node *start=new node,*end = new node; 11 int a[200000]; 12 13 int main(){ 14 end->data = -1; 15 ios::sync_with_stdio(false); 16 int n; 17 cin >> n; 18 for(int i=1;i<=n;i++) 19 cin>>a[i]; 20 start->next = end; 21 for(int i=1;i<=n;i++){ 22 int k=a[i]; 23 node *p = start; 24 while(p->next!=end&&p->next->data < k) 25 p = p->next; 26 node *q = p->next; 27 node *now = new node; 28 now->data = k; 29 now->next = q; 30 p->next = now; 31 } 32 node *p =start->next; 33 while(p!=end){ 34 cout<<p->data<<" "; 35 p = p->next; 36 } 37 return 0; 38 }
显然,这份代码也是O(n^2)的,慢在哪了?又是查找。
所以我们现在要做的事,就是把二分融合在链表里面,这就设下了一个大难关,但是,对数级的优化又启发了我们,我们必须在有限的次数(可以预知)内筛掉一半以上的数。
我们不妨考虑一个简化版的问题:给定n个有序的元素,现在要插入1个元素,用链表实现,效率是O(logn)怎么搞。
对这个问题,我有两个方法:
法1:在读入的时候预处理每个点到另一个点的中点的位置,空间复杂度高达O(n^2),铁定MLE。我们不得不另寻他法
法2:我们不妨分层存储,比如对于一个8个元素的链表,我们可以设计出以下数据结构: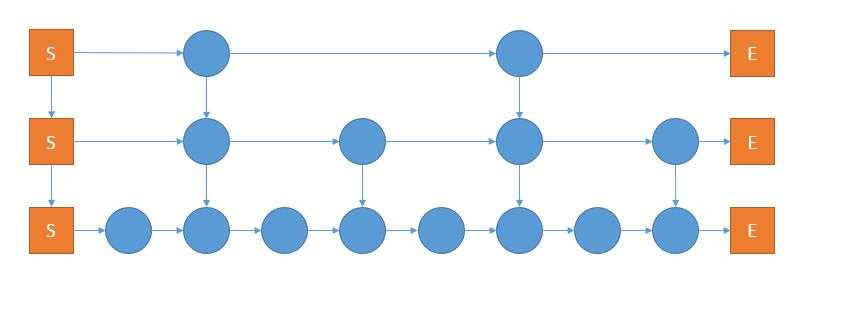
显然,层数是log2n层的,每一层的元素个数都是上一层的1/2,那么我们的查找显然是O(logn)的,我们从最顶上一层开始找,如果下一个不是我想要的,那么就排掉了一半,往下面走,以此类推。
这样的空间复杂度是O(n)的,显然第一层是有n个元素,此外每一层的元素个数都是上一层的1/2,回忆二叉树的知识,若我们在最上面再补一层,那么就有n+n-1=2n-1,那么再减去刚才补上的一层,就是2n-2个元素,所以空间复杂度是O(n)的。
推广这个问题,我们可以发现,这样子只能对某个固定的链表使用,而不能动态地更改,于是我们就想到了随机数。对每个元素,我们有1/2的几率让它成为上面一层的元素,这样的话每层元素的期望也就跟这个差不多,可以证明,这样做插入的复杂度是O(logn)<-递归log2n层,查找的复杂度也是O(logn),那么插入排序的复杂度就变成了O(nlogn),下面是代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstdlib> 4 #include<ctime> 5 #include<cstring> 6 using namespace std; 7 struct node{ 8 int data; 9 int level; //所在层数 10 node* under; //下一层的相同结点 11 node* next; 12 }; 13 struct llist{ //level of list 14 int level; 15 node* start; 16 llist(){ 17 start = new node; 18 start->data = -1; 19 } 20 }; 21 int siz[200]; //定义为一个天文数字 22 int a[200000]; 23 int log2(int); 24 node* end = new node; 25 int top = 1; //表示层数 26 llist le[200]; 27 int want,n; 28 int insert(int now,int lev,node* place,node *last = NULL){ 29 node *f = place; 30 while(f->next->data < now && f->next!=end) 31 f = f->next; 32 if(lev != 1){ 33 int pd = insert(now,lev-1,f->under,f); 34 if(pd == true){ 35 siz[lev]++; 36 int trid = rand()%2; 37 if(trid == 1){ 38 node* p = f->next; 39 node *q = new node; 40 q->data = p->data; 41 q->level = p->level+1; 42 q->under = p; 43 if(last!=NULL){ 44 q->next = last->next; 45 last->next = q; 46 }else{ 47 q->next = end; 48 le[lev+1].start->next = q; 49 } 50 if(siz[lev+1] == 0) 51 top = lev+1; 52 siz[lev+1] = 1; 53 return true; 54 } 55 }else 56 return false; 57 }else{ 58 siz[1]++; 59 node *p = new node; 60 p->level = 1; 61 p->data = now; 62 p->next = f->next; 63 f->next = p; //移花接木 64 int trid = rand()%2; 65 if(trid == 1&&lev<want){ 66 node *q = new node; 67 q->data = p->data; 68 q->level = p->level+1; 69 q->under = p; 70 if(last!=NULL){ 71 q->next = last->next; 72 last->next = q; 73 }else{ 74 q->next = end; 75 le[lev+1].start->next = q; 76 } 77 if(siz[lev+1] == 0) 78 top = lev+1; 79 siz[lev+1]++; 80 return 1; 81 }else 82 return 0; 83 } 84 } 85 86 int main(){ 87 freopen("sort.in","r",stdin); 88 freopen("sort.out","w",stdout); 89 srand(time(NULL)); 90 end->data = 2147483647; 91 end->level = -1; //确认身份 92 ios::sync_with_stdio(false); 93 cin >> n; 94 want = log2(n); 95 for(int i=1;i<=want;i++){ 96 le[i].level = i; 97 le[i].start->level = i; 98 le[i].start->next = end; 99 if(i!=1){ 100 le[i].start->under = le[i-1].start; 101 } 102 } 103 for(int i=1;i<=n;i++) 104 cin>>a[i]; 105 node* q = new node; 106 q->data = a[1]; 107 q->next = end; 108 le[1].start->next = q; //为第一层加上一个结点 109 siz[1]++; 110 for(int i=2;i<=n;i++){ 111 insert(a[i],top,le[top].start); //插 ♂入 a[i] 112 } 113 node *p = le[1].start; 114 p = p->next; 115 while(p!=end){ 116 cout<<p->data<<" "; 117 p = p->next; 118 } 119 return 0; 120 } 121 122 int log2(int n){ 123 int val = 1,k = 0; 124 while(val*2 < n){ 125 k++; 126 val*=2; 127 } 128 return k+1; 129 }
多美妙的代码啊。
下面是它与其它几种排序方法在时间上的比较:
首先是对于测试点的说明:
对于测试点1:n=100000,专门卡插入排序的测试点,因为是从小到大排序所以自然是从大到小的数据喽。
对于测试点2:n=1000,数据随机。基本上都能过
对于测试点3:n=10000,数据随机。卡卡常还是能过
对于测试点4:n=50000,数据随机。理论上分块能过,人懒就没写分块。
对于测试点5:n=100000,数据随机。只有O(nlogn)能过
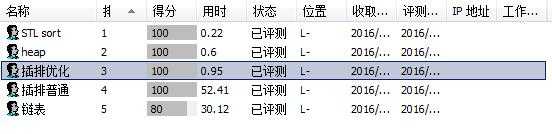
STL都跑得快,最慢的跑了0.09秒。heap_sort最慢的0.24秒。插排优化最慢的0.43秒(常数略大)。
普通插排最慢的32.18秒,被第一个点卡了。链表插排没过最后一个点(常数太大)。
还有一个我删了的是二分优化的普通插排(数组实现O(n^2)),最慢的跑了3秒。
下面是一道实战题,丑数(USACOtraining 第三章)
对于一给定的素数集合 S = {p1, p2, ..., pK},
来考虑那些质因数全部属于 S 的数的集合.这个集合包括,p1, p1p2, p1p1, 和 p1p2p3 (还有其它).
这是个对于一个输入的 S 的丑数集合.
注意:我们不认为 1 是一个丑数.
你的工作是对于输入的集合 S 去寻找集合中的第 N 个丑数.longint(signed 32-bit)对于程序是足
够的.
程序名: humble
读入说明:
第 1 行: 二个被空间分开的整数:K 和 N , 1<= K<=100 , 1<= N<=100,000.
第 2 行: K 个被空间分开的整数:集合 S 的元素
样例读入 (文件名 humble.in)
4 19
2 3 5 7
输出说明
单独的一行,写上对于输入的 S 的第 N 个丑数.
样例输出 (文件名 humble.out)
27
对于这道题,我们容易想到的一种做法是用堆来做,代码我就不贴了(其实就是我删了懒得重打了)。容易证明,这样做的复杂度是O(2^(k)*k*n)的,空间也是会爆掉的,所以这样做不行。
我们试着改变它,因为它是求第n小,所以假设一个由丑数构成的序列大于100000个元素,那么大于100,000的元素必然不可能是我想要的丑数(借用刘汝佳的一句话:想一想,为什么)。那么我们可以构建一个ans链表,来储存目前枚举出的每一个丑数,初始状态,ans数组仅有S集合中的元素,然后我们扫描一遍,求第n小,我们可以每次把当前第一小的数字出链表,同时加入它与它后面的数的乘积入链表(想一想为什么不加入它和前面的乘积,或者它和后面好几个的乘积),这个的复杂度显然是O(k*logn)的,如果这个链表大小超过了n,那么就砍尾巴喽。那么这个的复杂度就是O(n*k*logn),卡卡常还是能过的嘛。(毕竟是USACO,没像NOIP那样为难oier)。代码的话,我不会打!!!!毕竟这么晚了,改天有空了我会把代码补上。放心这次不会和前面那个三分,莫比乌斯一样烂尾的!
插入排序的优化【不靠谱地讲可以优化到O(nlogn)】 USACO 丑数
标签:
原文地址:http://www.cnblogs.com/1-1-1-1/p/5731990.html