标签:
假设m阶实对称阵X的低秩特征值分解为 , 其中U是列正交矩阵,即
,每一列为一个特征向量,S是对角阵,对角线上每个元素为特征值。r为分解的秩
1) 对X进行正交变换得到一个三对角阵T:,其中
2) 对T进行奇异值分解:
3) 最后 即为所求
1) T矩阵是一个三对角阵,很稀疏,因此对它的特征值分解会非常快。
2) 如果r很小,(求其最大的r个特征值),可以不用求整个T,而是求其左上1.5r阶的方阵即可得到很好的近似。这样对T的特征值分解会更快。(https://en.wikipedia.org/wiki/Lanczos_algorithm)
另外一种方法动态决定求多少lanzcos向量,http://peghoty.blog.163.com/blog/static/4934640920071179393238/
这里简单总结一下,初始选取n<m个lanzcos向量,然后求T的最大特征值和最小特征值,然后逐渐增加n,并更新这两个特征值,直到这种更新非常小为止。如果用在求r个主特征向量,那么可以更新第1个和第r个特征值。
我们知道,在幂迭代过程中,产生了一系列中间向量 。当v和X的任意特征向量都不正交的时候,这些向量构成的矩阵所张成的空间和X的特征向量所张成的空间相同。而且,随着迭代的进行,向量越来越趋近于主特征向量,而其他特征向量被逐 渐抛弃。其中特征值越小的,抛弃的越快。一个自然的想法就是,对前l个向量所构成的矩阵进行特征值分解,应该能得到原矩阵特征向量的近似解,l越大,越近似。当l=m-1时就得到了原矩 阵的特征向量。
然而,这种原始的方法并不稳定。因为较小的特征值被快速的抛弃,即使是第二大特征值,也是随迭代次数指数速度缩小(参看幂迭代收敛性证明,这里略过)。因此,为了能够保留小特 征值所张成的空间,需要在迭代中正交化,即在大特征值特征向量的正交空间中进行迭代。由此便产生了Arnoldi‘s algorithm,每次迭代所得向量都要去掉其和之前所有向量的投影。这个方法虽然稳定,但却要求次向量内积,相减。随着l增大,该方法速度堪忧。
lanczos提出了复杂度的正交化方法。由于X是实对称阵,可以证明,每次迭代得到的向量只需要和前两次得到的向量正交后,即可保证该向量和其他所有向量正交。并且将所有向量按列排列后得到的矩阵P,满足X=PTP‘,其中T为三对角阵。
详细来说,lanczos方法在每次迭代中,执行如下操作:
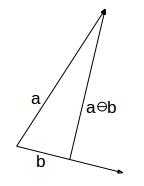
其中 表示 a在b的正交空间的投影:
论文 http://www.cs.cornell.edu/~bindel/class/cs6210-f09/lec32.pdf 解释了该方法实际上就是用迭代后的向量和前两次向量做正交,但是并没有证明这样得到的向量和其他向量一定正交和为什么得到的是三对角阵,本文在附录A中,给出了lanzcos方法的正交以及三对角性的证明。
三对角化后的矩阵T有三种常用的方法进行分解:
1) QR法,即对T进行QR分解,T=Q*R,其中Q为正交阵,R为上三角阵,然后令T‘=R*Q,如此反复进行,直至收敛。其中产生的Q矩阵的连乘就得到了T的特征向量。
文章https://www.math.kth.se/na/SF2524/matber15/qrmethod.pdf第二页给出了伪代码。在2.2.2节中,还提到了针对上海森伯格阵的快速QR算法,正好适用于这里的T矩阵。这里不再赘述。相比于另两种方法,QR方法并不高效,但是在求最大的少数特征向量时,T通常很小,因此为实现简单,以及稳定性考虑,QR方法常被使用。
2) 分治法。这个方法将T划均匀分成两块三对角阵和一个秩为1的2*2块状方阵的和。分别对两个三对角阵分解,然后合并。合并时对特征向量作秩1的修正。详细讨论见下一篇文章。
3) MRRR方法。这个方法是理论上最快的方法,O(l^2)复杂度,主要采用逆迭代来加快收敛。详细讨论见后续文章。
这里讨论大型、稀疏、非方阵A的奇异值分解的实现,并求其少数主奇异向量。主要从如下角度考虑:
1)对于非方阵的SVD可以转化为对称方阵,本文采用了通过对X=A*A‘的特征值分解从而得到A的奇异值分解的方法。X的特征向量即为A的左奇异向量,而A的右奇异向量可以通过左奇异向量左乘A得到。
2)由于矩阵非常大,不能完全读入内存,因此是存在硬盘上的。在计算lanzcos向量时,每次计算A*A‘*p需要扫两遍磁盘。A在磁盘上顺序存储,顺序读取,这样可以利用磁盘的读缓存。
3)考虑到多线程并行计算A*A‘*p,需要开辟读缓存,每次装载一批数据读入内存。每个线程维护自己的一个p向量,迭代完之后合并。
4)由于只求少数主奇异向量,因此lanzcos向量也不会很多(1.5倍于奇异向量数),因此可以假设lanzcos向量可以完全放在内存中。
本文中求lanzcos向量采用的是
https://en.wikipedia.org/wiki/Lanczos_algorithm
中的伪代码实现。由于lanczos方法并不稳定,迭代很多次之后,所得向量可能不正交甚至线性相关,关于lanzcos的重启即实现会在后续文章中讨论。
C++代码的实现见附录B.
首先引入一个符号,对于两个向量a,b, ,表示由a和b张成的空间中的某一个向量
证明:采用数学归纳法。需要证明两个命题
(1)正交性:
(2) 三对角:
先证明正交性。当k<=2时,结论显然成立。当k>2时,假设结论成立,则当k+1时,有
此时如果k>i+1,则根据归纳假设,;
否则如果k=i+1或者k=i(即k+1=i+2,或者k+1=i+1)时,根据的构造,直接可以得到
证明完毕。
再证明三对角性。当k<=2时,结论显然成立,当k>2时,假设结论成立,则当k+1时,对于i+1<k+1的任意i有
最后一个等号由正交性得出。
头文件svds.h定义了稀疏矩阵的结构以及函数接口,svds.cpp实现了基于lanzcos方法+QR方法的奇异值分解算法。这里lanzcos向量数并没有取1.5*r,而是计算所有向量。main.cpp实现了调用样例。
svds.h
#ifndef SVDS_H
#define SVDS_H
#include <vector>
using namespace std;
class Cell{
public:
unsigned int row;
unsigned int col;
double value;
Cell():row(0),col(0),value(0){};
Cell(int r, int c, double v):row(r),col(c),value(v){};
};
class SparseMatrix{
public:
unsigned int rows;
unsigned int cols;
vector<Cell> cells;
int cellID;
//read data sequentially, especially when loading large matrix from the disk.
void moveFirst(){
cellID=0;
}
bool hasNext(){
return cellID<cells.size();
}
Cell next(){
return cells[cellID++];
}
};
void svds(SparseMatrix &A, int r, vector<vector<double> > &U, vector<double> &s, vector<vector<double> > &V);
//decompose A = U * diag(s) *V‘
//where A is a m*n matrix
//U is a m*r column orthogonal matrix
//s is a length r vector
//V is a n*r column orthogonal matrix
void print(vector<vector<double> > &X);
#endif
svds.cpp
#include <iostream> #include <fstream> #include <vector> #include <string> #include <cmath> #include <climits> #include <cstdlib> #include <algorithm> #include "svds.h" using namespace std; const double EPS=1e-15; void print(vector<vector<double> > &X){ for(int i=0;i<X.size();i++){ for(int j=0;j<X[i].size();j++) cout<<X[i][j]<<‘ ‘; cout<<endl; } cout<<endl; } void randUnitVector(int n, vector<double> &v){ srand(time(NULL)); v.clear();v.resize(n); while(true){ double r=0; for(int i=0;i<n;i++){ v[i]=rand()*1.0/RAND_MAX-0.5; r+=v[i]*v[i]; } r=sqrt(r); if(r>EPS){ for(int i=0;i<n;i++) v[i]/=r; break; } } } void multiply(vector<vector<double> > &A, vector<vector<double> > &B, vector<vector<double> > &C){ //C=A*B for(int i=0;i<A.size();i++){ for(int j=0;j<B[0].size();j++){ C[i][j]=0; for(int k=0;k<A[0].size();k++){ C[i][j]+=A[i][k]*B[k][j]; } } } } void multiply(const vector<vector<double> > &X, const vector<double> & v, vector<double> & res){ res.clear(); if(X.empty() || v.empty()) return; int m=X[0].size(); res.resize(m,0); for(int i=0;i<m;i++){ for(int j=0;X[i].size();j++){ res[i]+=X[i][j]*v[j]; } } } double dotProduct(const vector<double> & a, const vector<double> & b){ double res=0; for(int i=0;i<a.size();i++) res+=a[i]*b[i]; return res; } void multiply(SparseMatrix &A, const vector<double> & v, vector<double> & res){ //res= A*A‘*v int m=A.rows; int n=A.cols; res.clear(); res.resize(m,0); vector<double> w(n,0); A.moveFirst(); while(A.hasNext()){ Cell c=A.next(); w[c.col]+=c.value*v[c.row]; } A.moveFirst(); while(A.hasNext()){ Cell c=A.next(); res[c.row]+=c.value*w[c.col]; } } void multiply(const vector<vector<double> > & B,SparseMatrix &A, vector<vector<double> > & C){ //C= B‘*A int m=B[0].size(); int k=B.size(); int n=A.cols; for(int i=0;i<C.size();i++) fill(C[i].begin(),C[i].end(),0); A.moveFirst(); while(A.hasNext()){ Cell c=A.next(); for(int i=0;i<m;i++){ C[c.col][i]+=c.value*B[c.row][i]; } } } double norm(const vector<double> &v){ double r=0; for(int i=0;i<v.size();i++) r+=v[i]*v[i]; return sqrt(r); } double normalize(vector<double> &v){ double r=0; for(int i=0;i<v.size();i++) r+=v[i]*v[i]; r=sqrt(r); if(r>EPS){ for(int i=0;i<v.size();i++) v[i]/=r; } return r; } void multiply(vector<double> &v, double d){ for(int i=0;i<v.size();i++) v[i]*=d; } void QR(vector<vector<double> > &A, vector<vector<double> > &Q, vector<vector<double> > &R){ //A=Q*R //A: m*n matrix //Q: m*m matrix //R: m*n matrix int m=A.size(); int n=A[0].size(); for(int i=0;i<Q.size();i++) fill(Q[i].begin(),Q[i].end(),0); for(int i=0;i<R.size();i++) fill(R[i].begin(),R[i].end(),0); vector<double> q(m); vector<double> r(n); for(int i=0;i<n;i++){ for(int j=0;j<m;j++) q[j]=A[j][i]; fill(r.begin(),r.end(),0); for(int j=0;j<i && j<m;j++){ r[j]=0; for(int k=0;k<q.size();k++) r[j]+=Q[k][j]*q[k]; for(int k=0;k<q.size();k++) q[k]-=Q[k][j]*r[j]; } if(i<m){ r[i]=normalize(q); for(int j=0;j<m;j++) Q[j][i]=q[j]; } for(int j=0;j<m;j++){ R[j][i]=r[j]; } } } void lanczos(SparseMatrix &A, vector<vector<double> > &P, vector<double> &alpha, vector<double> &beta, unsigned int rank){ //P‘*A*A‘*P = T = diag(alpha) + diag(beta,1) + diag(beta, -1) //P=[p1,p2, ... , pk] rank=min(A.cols,min(A.rows,rank)); vector<double> p; unsigned int m=A.rows; unsigned int n=A.cols; vector<double> prevP(m,0); randUnitVector(m,p); P.clear(); P.resize(m,vector<double>(rank,0)); vector<double> v; alpha.clear();alpha.resize(rank); beta.clear();beta.resize(rank); beta[0]=0; for(int i=0;i<rank;i++){ for(int j=0;j<p.size();j++){ P[j][i]=p[j]; } multiply(A, p, v); alpha[i]=dotProduct(p,v); if(i+1<rank){ for(int j=0;j<m;j++) v[j]=v[j]-beta[i]*prevP[j]-alpha[i]*p[j]; beta[i+1]=norm(v); prevP=p; for(int j=0;j<m;j++) p[j]=v[j]/beta[i+1]; } } } void svds(SparseMatrix &A, int r, vector<vector<double> > &U, vector<double> &s, vector<vector<double> > &V){ //A=U*diag(s)*V‘ //A:m*n matrix sparse matrix //U:m*r matrix, U[i]=i th left singular vector //s:r vector //V:n*r matrix, V[i]=i th right singular vector int m=A.rows; int n=A.cols; //lanczos: A*A‘=P*T*P‘ int l=min(m,n); //int l=min(2*r,m); vector<vector<double> > P(m,vector<double>(l,0)); vector<double> alpha(l,0); vector<double> beta(l,0); lanczos(A,P,alpha,beta,l); vector<vector<double> > T(l,vector<double>(l,0)); for(int i=0;i<l;i++){ T[i][i]=alpha[i]; if(i) T[i-1][i]=T[i][i-1]=beta[i]; } vector<vector<double> > Q(l,vector<double>(l,0)); vector<vector<double> > R(l,vector<double>(l,0)); vector<vector<double> > W(l,vector<double>(l,0)); vector<vector<double> > nextW(l,vector<double>(l,0)); for(int i=0;i<l;i++) W[i][i]=1; while(true){ //T=Q*R QR(T,Q,R); //T=R*Q multiply(R,Q,T); //W=W*Q; multiply(W,Q,nextW); double diff=0; for(int i=0;i<l;i++) for(int j=0;j<l;j++) diff+=(W[i][j]-nextW[i][j]) * (W[i][j]-nextW[i][j]); W=nextW; if(diff<EPS*EPS) break; } U.clear();U.resize(m,vector<double>(l)); multiply(P,W,U); for(int i=0;i<U.size();i++) U[i].resize(r); V.clear();V.resize(n,vector<double>(r)); multiply(U,A,V); s.clear();s.resize(r,0); for(int i=0;i<r;i++){ for(int j=0;j<n;j++) s[i]+=V[j][i]*V[j][i]; s[i]=sqrt(s[i]); if(s[i]>EPS){ for(int j=0;j<n;j++) V[j][i]/=s[i]; } } }
main.cpp
#include "svds.h"
#include <iostream>
#include <cstdlib>
int main(){
srand(time(NULL));
SparseMatrix A;
A.rows=10;
A.cols=8;
for(int i=0;i<A.rows;i++){
for(int j=0;j<A.cols;j++){
A.cells.push_back(Cell(i,j,rand()*1.0/RAND_MAX-0.5));
}
}
vector<vector<double> > U,V;
vector<double> s;
svds(A,4,U,s,V);
cout<<"A = "<<endl;
A.moveFirst();
for(int i=0;i<A.rows;i++){
for(int j=0;j<A.cols;j++)
cout<<A.next().value<<‘ ‘;
cout<<endl;
}
cout<<endl<<endl;
cout<<"U = "<<endl;
print(U);
cout<<"s = ";
for(int i=0;i<s.size();i++)
cout<<s[i]<<‘ ‘;
cout<<endl;
cout<<endl;
cout<<"V = "<<endl;
print(V);
return 0;
}
基于lanzcos方法的特征值分解算法原理及C++实现(一):lanzcos方法原理以及简单实现
标签:
原文地址:http://www.cnblogs.com/qxred/p/lanzcos.html