标签：
| Time Limit: 3000MS | Memory Limit: 131072K | |
| Total Submissions: 23064 | Accepted: 4987 |
Description
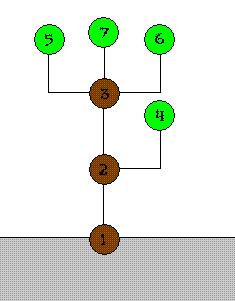Christmas is coming to KCM city. Suby the loyal civilian in KCM city is preparing a big neat Christmas tree. The simple structure of the tree is shown in right picture.
The tree can be represented as a collection of numbered nodes and some edges. The nodes are numbered 1 through n. The root is always numbered 1. Every node in the tree has its weight. The weights can be different from each other. Also the shape of every available edge between two nodes is different, so the unit price of each edge is different. Because of a technical difficulty, price of an edge will be (sum of weights of all descendant nodes) × (unit price of the edge).
Suby wants to minimize the cost of whole tree among all possible choices. Also he wants to use all nodes because he wants a large tree. So he decided to ask you for helping solve this task by find the minimum cost.
Input
The input consists of T test cases. The number of test cases T is given in the first line of the input file. Each test case consists of several lines. Two numbers v, e (0 ≤ v, e ≤ 50000) are given in the first line of each test case. On the next line, v positive integers wi indicating the weights of v nodes are given in one line. On the following e lines, each line contain three positive integers a, b,c indicating the edge which is able to connect two nodes a and b, and unit price c.
All numbers in input are less than 216.
Output
For each test case, output an integer indicating the minimum possible cost for the tree in one line. If there is no way to build a Christmas tree, print “No Answer” in one line.
Sample Input
2 2 1 1 1 1 2 15 7 7 200 10 20 30 40 50 60 1 2 1 2 3 3 2 4 2 3 5 4 3 7 2 3 6 3 1 5 9
Sample Output
15 1210
Source
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
const int maxn=50000+5;
const long long INF=0x3f3f3f3f3f;
int weight[maxn];
int cnt;
int head[maxn];
long long dis[maxn];
bool vis[maxn];
int n,m;
struct Edge
{
int to,w,next;
} edge[maxn<<1];
struct Node
{
int u,dis;
// 此处的dis仅仅是为了使用优先队列：定义优先级
bool operator <(const Node &a) const
{
return dis>a.dis;
// 当返回true时会更新堆，因此当新元素a的dis小于堆顶元素dis
// 的时候会返回true，同时会更新堆，故此堆为小顶堆
}
};
void Init()
{
cnt=0;
memset(head,-1,sizeof(head));
memset(vis,false,sizeof(vis));
for(int i=0; i<=n; i++)
dis[i]=INF;
}
void addEdge(int u,int v,int w)
{
edge[cnt].to=v;
edge[cnt].w=w;
edge[cnt].next=head[u];
head[u]=cnt++;
}
void Dijkstra(int s)
{
Node now,next;
priority_queue<Node>q;
now.dis=0;
now.u=s;
dis[s]=0;
q.push(now);
while(!q.empty())
{
now=q.top();
q.pop();
if(vis[now.u])
continue;
int u=now.u;
vis[u]=true;
for(int i=head[u]; i!=-1; i=edge[i].next)
{
int to=edge[i].to;
//对点v，会有多个dis存在，不过我们只取对顶元素，
//即dis最小的点v
if(!vis[to]&&dis[u]+edge[i].w<dis[to])
{
dis[to]=dis[u]+edge[i].w;
next.dis=dis[to];
next.u=to;
q.push(next);
}
}
}
}
int main()
{
int T;
cin>>T;
while(T--)
{
cin>>n>>m;
Init();
for(int i=1; i<=n; i++)
scanf("%d",&weight[i]);
int u,v,w;
for(int i=1; i<=m; i++)
{
scanf("%d%d%d",&u,&v,&w);
addEdge(u,v,w);
addEdge(v,u,w);
}
Dijkstra(1);
long long sum=0;
bool flag=true;
for(int i=2; i<=n; i++)
{
if(dis[i]==INF)
{
flag=false;
break;
}
sum+=dis[i]*weight[i];
}
if(flag)
cout<<sum<<endl;
else
cout<<"No Answer"<<endl;
}
return 0;
}
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
const int maxn=50000+5;
const __int64 INF=0x3f3f3f3f3f;
int weight[maxn];
int cnt;
int head[maxn];
__int64 dis[maxn];
bool vis[maxn];
int n,m;
struct Edge
{
int to,next,w;
}edge[maxn<<1];
void Init(void)
{
cnt=0;
memset(head,-1,sizeof(head));
memset(vis,false,sizeof(vis));
for(int i=0;i<=n;i++)
dis[i]=INF;
}
void addEdge(int u,int v,int w)
{
edge[cnt].to=v;
edge[cnt].w=w;
edge[cnt].next=head[u];
head[u]=cnt++;
}
void spfa(int s)
{
queue<int>q;
q.push(s);
vis[s]=true;
dis[s]=0;
while(!q.empty())
{
int p=q.front();
q.pop();
vis[p]=false;
//
for(int i=head[p];i!=-1;i=edge[i].next)
{
int to=edge[i].to;
int w=edge[i].w;
if(dis[p]+w<dis[to])
{
dis[to]=dis[p]+w;
if(!vis[to])
{
q.push(to);
vis[to]=true;
}
}
}
}
}
int main()
{
int T;
cin>>T;
while(T--)
{
cin>>n>>m;
Init();
for(int i=1; i<=n; i++)
scanf("%d",&weight[i]);
int u,v,w;
for(int i=1; i<=m; i++)
{
scanf("%d%d%d",&u,&v,&w);
addEdge(u,v,w);
addEdge(v,u,w);
}
//Dijkstra(1);
spfa(1);
__int64 sum=0;
bool flag=true;
for(int i=2; i<=n; i++)
{
if(dis[i]==INF)
{
flag=false;
break;
}
sum+=dis[i]*weight[i];
}
if(flag)
cout<<sum<<endl;
else
cout<<"No Answer"<<endl;
}
return 0;
}
POJ 3013 Big Christmas Tree【最短路变形，DIjkstra堆优化+spfa算法】
标签：
原文地址：http://blog.csdn.net/hurmishine/article/details/52163677
