标签:
# 题目
There are two sorted arrays nums1 and nums2 of size m and n respectively.
Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).
Example 1:
nums1 = [1, 3] nums2 = [2] The median is 2.0
Example 2:
nums1 = [1, 2] nums2 = [3, 4] The median is (2 + 3)/2 = 2.5
# 思路
两指针填充数组法:
想法来源于插入排序的过程。插入排序每一次将一位数字之前插入有序数组之中。
例如{1, 3, 4, 2},前面三位已用插入排序排序完毕,第四位2首先和1比较,大于,再和后面一位比较,小于,故放入该位置,其余元素后移。
此题的算法:
首先,把指针index1指向nums1,指针Index2指向nums2,同时创建一个数组sum,用来保存两个数组按照大小合并的结果。
接着,比较index1和index2所指元素的大小,sum数组填充两者较小的一个,同时指向较小元素的指针后移一位。
反复上面一步,当sum填充到中间时,结束,根据奇偶,计算中间值。
举个例子:
比如nums1 = {1, 3},nums2 = {2, 4, 5},index1指向nums1中的1,index2指向nums2中的2,1 < 2,所以sum填充1。
此时index1后移指向3,3 > 2,sum填充2,index2后移。此时index2指向4,4 > 3,sum填充3。此时sum已经填充到中部,故直接输出3。
// use two pointers to construct full nums including nums1 and nums2 // two pointers: time O(m+n) space O(n) result: 255ms public double FindMedianSortedArrays(int[] nums1, int[] nums2) { int[] sum; // nums1 is null or num2 is null if (nums1.Length == 0) sum = nums2; else if (nums2.Length == 0) sum = nums1; else sum = new int[nums1.Length + nums2.Length]; // user 2 pointers to find middle numbers int length = nums1.Length + nums2.Length, index1 = 0, index2 = 0, index = 0; for (; index < sum.Length && index1 < nums1.Length && index2 < nums2.Length; index++) { if (nums1[index1] < nums2[index2]) sum[index] = nums1[index1++]; else sum[index] = nums2[index2++]; } for (; index1 < nums1.Length; index++, index1++) sum[index] = nums1[index1]; for (; index2 < nums2.Length; index++, index2++) sum[index] = nums2[index2]; if (length % 2 != 0) return sum[length / 2]; else return (double)(sum[length / 2 - 1] + sum[length / 2]) / 2; }
两指针填充数组法,时间复杂度O(m + n),空间复杂度O(n),时间255ms。
算法虽然AC(Accept)了,可并不满足题中所给的时间复杂度O(lg(m + n))。谈到lg,即以2为底的对数,很容易联想到对半的思想,二分查找法。
然而我并想不出来如何二分。
去LeetCode的Discuss区看了一下。发现了这样一个算法:二分查找,划分两数组法。参考地址:https://discuss.leetcode.com/topic/4996/share-my-o-log-min-m-n-solution-with-explanation/90。
天才。
只说说大概流程,具体内容直接参考链接,不懂请大胆留言。
算法的主要目的是将nums1和nums2形式意义上合并,再划分成两个规模相等且右侧所有数字大于左侧所有数字的数组(利用指针标记划分的位置),再根据划分的位置(由于两部分规模相等,必然是中间元素),输出结果。
如下图,我们先确定划分位置,这个划分位置一定会将左右两侧等分。

之后我们要保证左侧所有元素小于右侧所有元素,由于nums1和nums2是有序数组,边界元素就是划分之中最大/最小的元素,所以我们只需要关注边界即可。
假设nums1划分的位置是i,nums2划分的位置是j,要满足左侧元素小于右侧所有元素,必须满足nums1[i - 1] < nums1[i](数组有序,必定满足),nums1[i - 1] < nums2[j],nums1[i] > nums2[j - 1],nums2[j - 1] < nums2[j](数组有序,必定满足)。
若不满足nums1[i - 1] < nums2[j],如图,重新确定划分位置(图只是重划分的位置只是减少了1,实际上重划分的位置采用二分法)。

若不满足nums1[i] > nums2[j - 1],如图,重新确定划分位置(图只是重划分的位置只是减少了1,实际上重划分的位置采用二分法)。
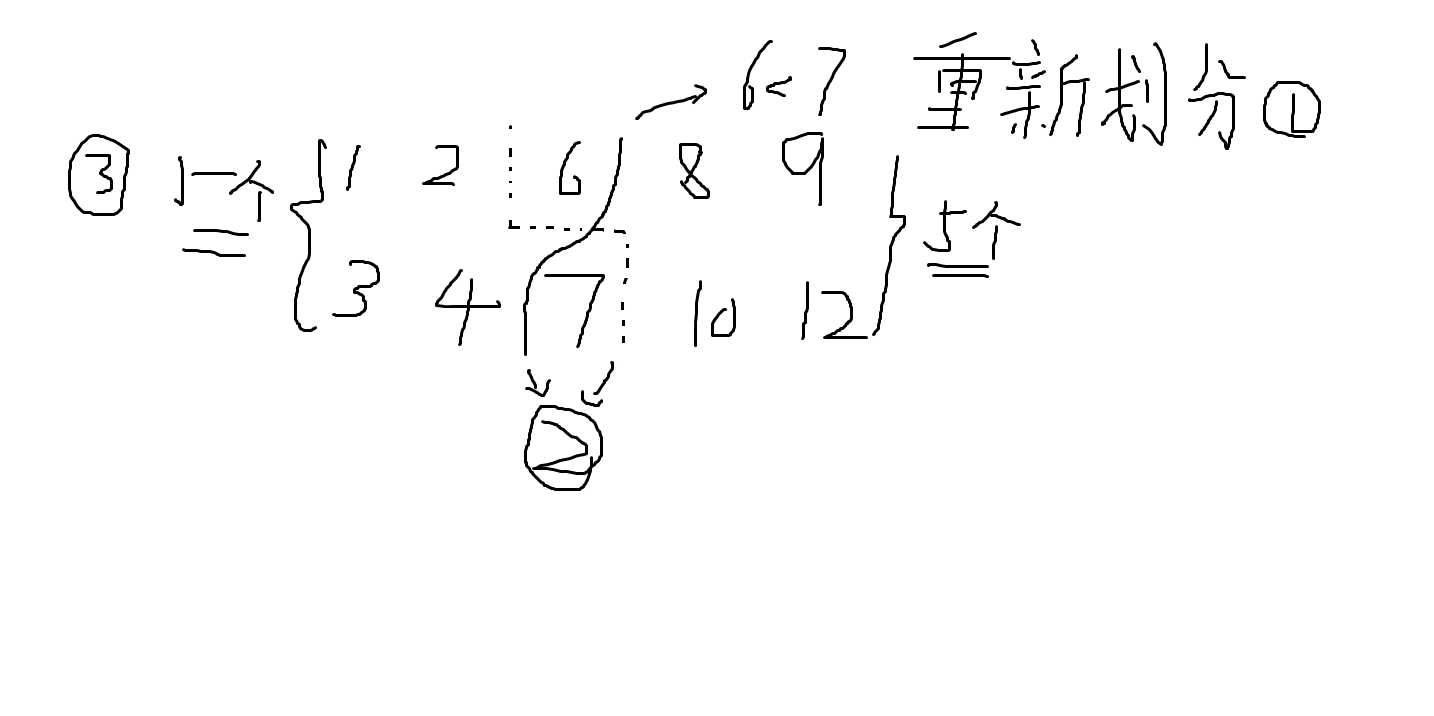
反复上述过程,最后我们可以得到中间值。

# 解决(二分查找,划分两数组法)
// reference: https://discuss.leetcode.com/topic/4996/share-my-o-log-min-m-n-solution-with-explanation/ // time: O(lg(min(nums1,nums2)) space: O(1) result: 228ms public double FindMedianSortedArrays(int[] nums1, int[] nums2) { if (nums1.Length == 0 && nums2.Length == 0) throw new Exception("none value in nums1 and nums2"); if (nums1.Length == 0 && nums2.Length % 2 == 0) return (double)(nums2[nums2.Length / 2 - 1] + nums2[nums2.Length / 2]) / 2; if (nums1.Length == 0 && nums2.Length % 2 != 0) return (double)nums2[nums2.Length / 2]; if (nums2.Length == 0 && nums1.Length % 2 == 0) return (double)(nums1[nums1.Length / 2 - 1] + nums1[nums1.Length / 2]) / 2; if (nums2.Length == 0 && nums1.Length % 2 != 0) return (double)nums1[nums1.Length / 2]; if (nums1.Length > nums2.Length) return FindMedianSortedArrays(nums2, nums1); int imin = 0, imax = nums1.Length, midLength = (nums1.Length + nums2.Length + 1) / 2; int i, j; // when i isn‘t the split must satisfy below condition do { i = (imin + imax) / 2; j = midLength - i; if (i > 0 && j < nums2.Length && nums1[i - 1] > nums2[j]) imax--; // nums[i - 1] > nums[j] means imin is too samll else if (i < nums1.Length && j > 0 && nums1[i] < nums2[j - 1]) imin++; // nums1[i] < nums2[j - 1] means imax is small else break; } while (true); // i is split, so we get answer by conditon // get left first int left; if (i == 0) left = nums2[j - 1]; else if (j == 0) left = nums1[i - 1]; else left = nums1[i - 1] > nums2[j - 1] ? nums1[i - 1] : left = nums2[j - 1]; // sum length is odd if ((nums1.Length + nums2.Length) % 2 != 0) { return (double)left; } else { int right; if (i == nums1.Length) right = nums2[j]; else if (j == nums2.Length) right = nums1[i]; else right = nums1[i] < nums2[j] ? nums1[i] : nums2[j]; return (double)(left + right) / 2; } }
二分查找,划分两数组法,时间复杂度O(lg(m + n)),空间复杂度O(1),时间228ms。
# 题外话
图够丑吗?来喷我啊,嘿嘿?
# 测试用例
static void Main(string[] args) { _4MedianofTwoSortedArrays solution = new _4MedianofTwoSortedArrays(); Debug.Assert(solution.FindMedianSortedArrays(new int[] { 1, 3 }, new int[] { 2 }) == 2.0d, "wrong 1"); // odd Debug.Assert(solution.FindMedianSortedArrays(new int[] { 2 }, new int[] { 1, 3 }) == 2.0d, "wrong 2"); // odd Debug.Assert(solution.FindMedianSortedArrays(new int[] { 1, 2 }, new int[] { 2, 3 }) == 2.0d, "wrong 3"); // even and duplication Debug.Assert(solution.FindMedianSortedArrays(new int[] { 1, 3 }, new int[] { 2, 4 }) == 2.5d, "wrong 4"); // even Debug.Assert(solution.FindMedianSortedArrays(new int[] { }, new int[] { 2, 5 }) == 3.5d, "wrong 5"); // nums1 null Debug.Assert(solution.FindMedianSortedArrays(new int[] { 1, 3 }, new int[] { }) == 2d, "wrong 6"); // nums2 numm Debug.Assert(solution.FindMedianSortedArrays(new int[] { 1, 2, 3, 4, 5, 6 }, new int[] { 7 }) == 4d, "wrong 7"); // only nums1 pointer move Debug.Assert(solution.FindMedianSortedArrays(new int[] { 7 }, new int[] { 1, 2, 3, 4, 5, 6, 7 }) == 4.5d, "wrong 8"); // only nums2 pointer move Debug.Assert(solution.FindMedianSortedArrays(new int[] { 1, 3, 7 }, new int[] { 1, 2, 4, 4, 8 }) == 3.5d, "wrong 9"); Debug.Assert(solution.FindMedianSortedArrays(new int[] { 1, 3 }, new int[] { 1, 2, 4, 4, 8 }) == 3d, "wrong 10"); }
# 地址
Q: https://leetcode.com/problems/median-of-two-sorted-arrays/
A: https://github.com/mofadeyunduo/LeetCode/tree/master/4MedianofTwoSortedArrays
(希望各位多多支持本人刚刚建立的GitHub和博客,谢谢,有问题可以邮件609092186@qq.com或者留言,我尽快回复)
LeetCode-4MedianofTwoSortedArrays(C#)
标签:
原文地址:http://www.cnblogs.com/Piers/p/5762947.html