标签:
这是一篇简单的匈牙利算法的理解篇,首先匈牙利算法的名字听起来就和匈牙利牛肉饭一样让人产生食欲(?)233。
好的接下来我们开始正式带大家了解什么叫匈牙利算法。
那么要了解算法的基本原理,我们先看一张图
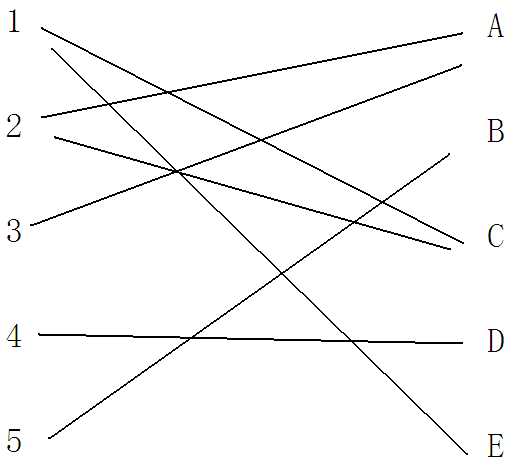
在这张图里,我们可以清楚的看出图上的点被我们分成了两种,一种是数字,另一种是字母,并且数字与数字、字母与字母之间是没有互相连接的边的,这种点被划为两种、且每种之间没有连边的图就叫做二分图,而我们的匈牙利算法就是用来处理二分图匹配的。
什么叫二分图匹配捏,很简单,我们从这张图中选出一些边,举个例子,我们选出1——C,2——A,4——D这三条边,使得每条边对应左右两边各一个点,且对于每个点来说,边唯一。
而对于匈牙利算法来说,它求的是二分图最大匹配,什么叫最大匹配捏,就是说在二分图中选择尽可能多的边,使它们遵从二分图匹配的规则,如果我们选择的边数为全图点数除以2的话,则叫做完全匹配。
那么匈牙利算法具体怎么实现捏?具体如以下图示
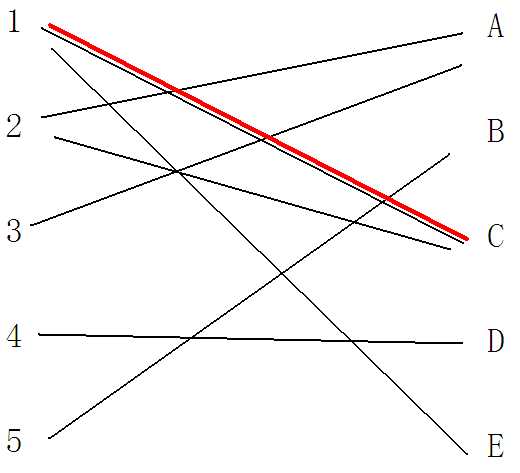
首先我们找到左边的1,从1出发选择1能连到的第一条边为1——C(上图中标红的边)
具体为我们从左边第一个没有连到边的点(如原始图所示为1)开始搜索,找到第一个可以连到的点C,然后选择连接两个点,记录连接点C的是1。
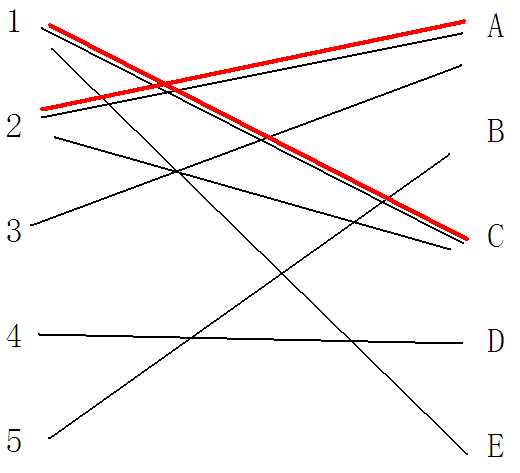
接下来找到第二个点2,同样连接 2 和 与2连接的第一个没有被连接过的点(如上图所示为A),记录连接点A的是2。
重点!!!!!
接下来就是匈牙利算法的精髓所在,因为从3开始连接的时候我们就开始慌了,唯一和3连接的点A已经被连过了,那么接下来就是展现匈牙利算法的威力的时刻啦哈哈哈哈哈哈哈(蜜汁笑声)
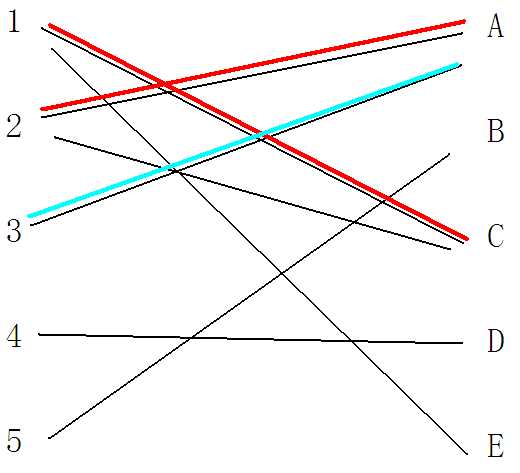
那么我们要做的是用深度优先搜索找出首先找出与当前失匹配点3所能联通的点(上图青色边为我们深搜的过程路径),那么当前所找到的就为A,因为A已经被连接,所以我们可以直接找到连接A的是2,然后继续深搜。
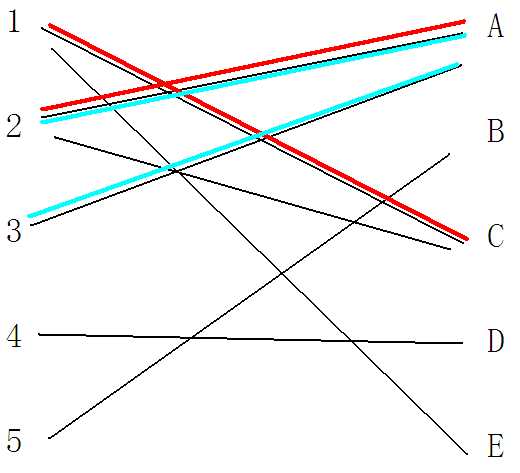
然后继续从2开始搜索,找一条能与2连接,并且不是当前来的路径(2——A)的另一条路径(根据匈牙利算法,如果这里找不到就返回上一层,知道搜索完深度优先搜索开始节点3的每一条边,如果都找不到就判断这次算法执行没有更优结果),那么显然的,我们找到了C这个点。
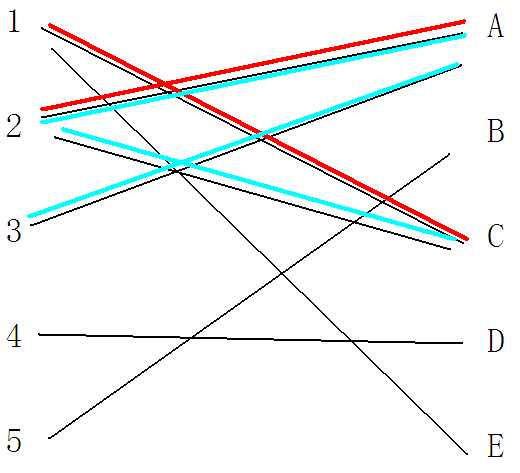
同样的,我们之前记录过连接C的节点(也就是1),那么继续以1开始搜索与1连接,并且不是1——C这条路径的另一条路径,
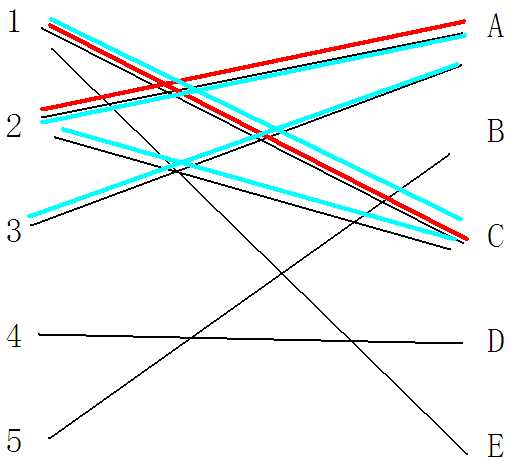
显然的,找到1——E这条路径,然后对点E进行判断。
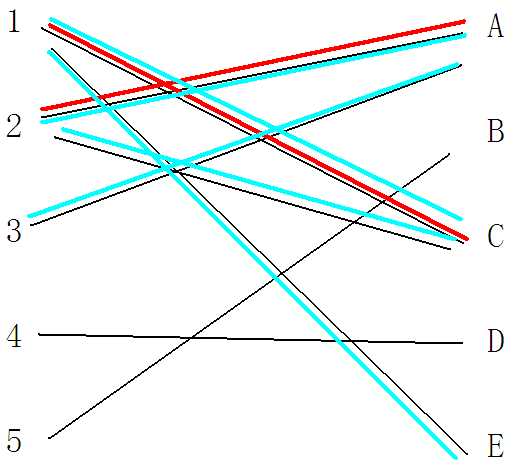
这时我们发现E是没有其他路径与其他点连接的,那么这时我们开始return,那么看,此时图中所有标为青色的边是我们的搜索路径,那么我们在return时要做的事情就是:把所有{只标青而没有变红的边}变为新的连接边,而吧所有{又标红又标青的边}取消连接.
那么这时图就变成
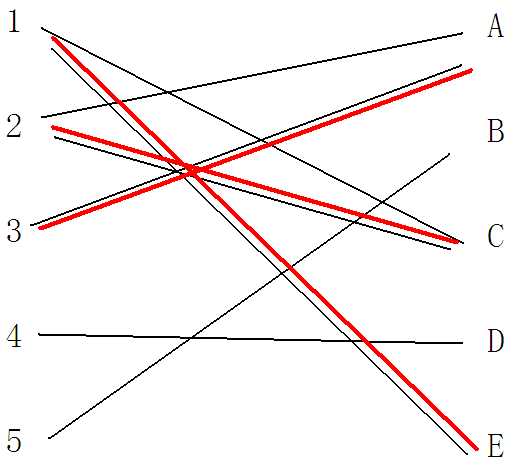
那么对于当前情况,我们就相当于完成了局部最优匹配,然后接下来就是继续按照这种方法完成全图最优匹配就好了。
那么完成图就为
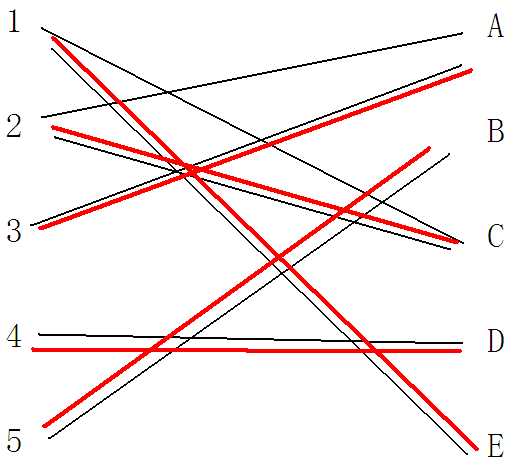
这时我们就求出了二分图最大匹配
(PS写在最后,我们是要记录:{每次连接边后,成功连接右边某个点的左边点的位置},同时如果我们做的找到环的话就只能回到上一层,所以要记录{哪些点在当前搜索中用到},这样下次搜索就不会死循环)
附上一道水题,codevs1022 http://codevs.cn/problem/1022/
那么这道题里面,我们把所有格子按国际象棋棋盘的染色法进行染色,使得与黑相邻的所有点都为白色,与白色相邻的点都为黑色,然后把所有没有被水淹的格子按黑白做一个二分图,那么每个格子一开始的路径就为与它四周不出界且没有被水淹的格子连接所产生的路径,然后单纯的做匈牙利算法就好了呀。
然后贴出代码(PS蜜汁变量名和谐修改)
1 #include<stdio.h> 2 int xx[4]={0,1,0,-1},yy[4]={1,0,-1,0}; 3 bool usd[110][110],map[110][110],wat[110][110]; 4 int n,m,k,from[110][110][3],ans; 5 bool find(int x,int y) 6 { 7 int k; 8 for(k=0;k<4;k++) 9 { 10 int xi=x+xx[k],yi=y+yy[k]; 11 if(xi<1||xi>n||yi<1||yi>m)continue; 12 if(!map[xi][yi]&&!usd[xi][yi]&&!wat[xi][yi]) 13 { 14 usd[xi][yi]=true; 15 if(!from[xi][yi][0]||find(from[xi][yi][0],from[xi][yi][1])) 16 { 17 from[xi][yi][0]=x; 18 from[xi][yi][1]=y; 19 return true; 20 } 21 } 22 } 23 return false; 24 } 25 int main() 26 { 27 int a,b; 28 scanf("%d%d%d",&n,&m,&k); 29 for(int i=1;i<=k;i++) 30 { 31 scanf("%d%d",&a,&b); 32 wat[a][b]=true; 33 } 34 for(int i=1;i<=n;i++) 35 for(int j=1;j<=m;j++) 36 { 37 if(i%2==0&&j%2==0)map[i][j]=true; 38 if(i%2&&j%2)map[i][j]=true; 39 } 40 for(int i=1;i<=n;i++) 41 { 42 for(int j=1;j<=m;j++) 43 { 44 if(!wat[i][j]&&map[i][j]) 45 { 46 for(int ii=1;ii<=n;ii++) 47 for(int jj=1;jj<=m;jj++) 48 usd[ii][jj]=false; 49 if(find(i,j)) 50 { 51 ans++; 52 } 53 } 54 } 55 } 56 printf("%d",ans); 57 return 0; 58 }
标签:
原文地址:http://www.cnblogs.com/PencilWang/p/5769385.html