标签:
恩..接着就是Cyrus-Beck算法。这个算法比之前的Cohen-Sutherland算法厉害,处理任意凸多边形对线段的裁剪。自然,这个算法也比Cohen-Sutherland算法复杂不少。
首先,是线段与多边形相交的情况:
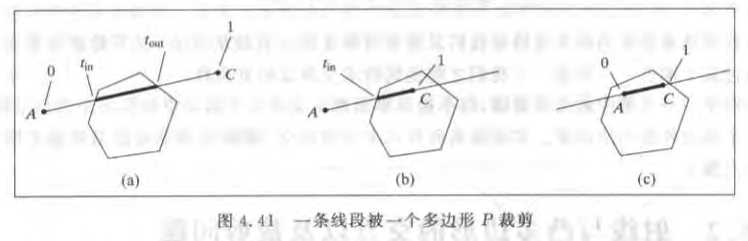
我们把定义向量c = (C - A),而线段AC是射线A + ct的一部分。那么t取0和1就是线段AC。我们将射线与多边形的每条边求出相交时的t。取tin = max(0, tin),tout = max(tout, 1)。最终会获得一个区间[tin,tout]就是经多边形裁剪后的线段。通过A+ct即可还原出裁剪后的线段。
那么怎么判断射线与多边形某一边相交时是射入还是射出呢,这就得先求出多边形的每条边的法向量了。规定法向量全部朝向多边形的外部。那么射线与该边的法向量的点积小于0,即夹角大于90°,肯定是射入;点积大于0,即夹角小于90°,则是射出。
于是问题就是怎么求出每条边的法向量。由于我们规定了多边形是凸的,并且法向量均指向外部,那么法向量与跟它相邻的边的夹角一定是在90°~180°之间,即点积小于0。故我们只要任意求出一个向量与这条边垂直,然后算它与下一条边的点积,如果大于零就把它反转方向即可。
一个例子如下:
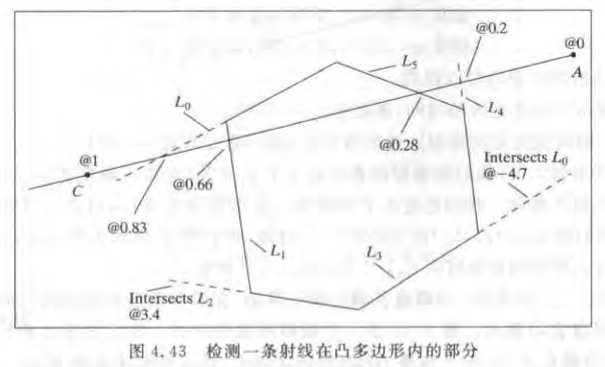
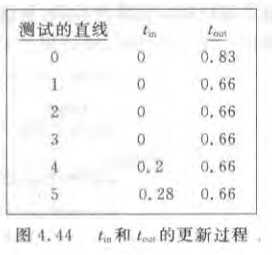
接下就是代码了:

1 #include <GL/gl.h> 2 #include <GL/glu.h> 3 #include <GL/glut.h> 4 #include <iostream> 5 #include <vector> 6 #include <cmath> 7 using namespace std; 8 9 struct Point2D 10 { 11 float _x, _y; 12 Point2D() 13 { 14 _x = 0.0f; 15 _y = 0.0f; 16 } 17 Point2D(const Point2D& p) 18 { 19 _x = p._x; 20 _y = p._y; 21 } 22 Point2D(float xx, float yy) 23 { 24 _x = xx; 25 _y = yy; 26 } 27 Point2D& operator=(const Point2D& p) 28 { 29 _x = p._x; 30 _y = p._y; 31 return *this; 32 } 33 Point2D& operator+(const Point2D& p) 34 { 35 Point2D temp; 36 temp._x = _x + p._x; 37 temp._y = _y + p._y; 38 return temp; 39 } 40 Point2D& operator-(const Point2D& p) 41 { 42 Point2D temp(_x - p._x, _y - p._y); 43 return temp; 44 } 45 float operator*(const Point2D& p) 46 { 47 return _x * p._x + _y * p._y; 48 } 49 50 Point2D operator*(const float k) 51 { 52 return Point2D(_x * k, _y * k); 53 } 54 55 float length() 56 { 57 return sqrtf(_x * _x + _y * _y); 58 } 59 60 void InverseDir() 61 { 62 _x = -_x; 63 _y = -_y; 64 } 65 }; 66 67 struct Line2D 68 { 69 Point2D _start; 70 Point2D _end; 71 float _length; 72 73 Line2D() : _start(), _end() 74 { 75 _length = 0.0f; 76 } 77 Line2D(const Point2D& start, const Point2D& end) : _start(start), _end(end) 78 { 79 } 80 Line2D(const Line2D& line) : _start(line._start), _end(line._end) 81 {} 82 83 float length() 84 { 85 _length = (_end - _start).length(); 86 } 87 88 Line2D& operator = (const Line2D& line) 89 { 90 _start = line._start; 91 _end = line._end; 92 } 93 94 Point2D GetVector() 95 { 96 return _end - _start; 97 } 98 }; 99 100 struct Rect 101 { 102 float _left; 103 float _right; 104 float _up; 105 float _down; 106 107 float width() 108 { 109 return _right - _left; 110 } 111 float height() 112 { 113 return _down - _up; 114 } 115 }; 116 117 struct Polygon 118 { 119 int _num;//Num of lines, not points 120 Point2D* points; 121 Point2D* norms; 122 123 Polygon() 124 { 125 _num = 0; 126 } 127 Polygon(vector<Point2D> p) 128 { 129 Set(p); 130 } 131 ~Polygon() 132 { 133 delete[] points; 134 } 135 136 void Clear() 137 { 138 delete[] points; 139 } 140 141 void Set(vector<Point2D> p) 142 { 143 _num = p.size(); 144 points = new Point2D[_num]; 145 for(int i = 0; i < _num; ++i) 146 points[i] = p[i]; 147 148 norms = new Point2D[_num]; 149 ComputeNormals(); 150 } 151 152 Line2D GetLine(int index) 153 { 154 Line2D temp; 155 if(index >= 0 && index < _num - 1) 156 { 157 temp._start = points[index]; 158 temp._end = points[index + 1]; 159 } 160 else if(index == _num - 1) 161 { 162 temp._start = points[index]; 163 temp._end = points[0]; 164 } 165 return temp; 166 } 167 168 Point2D GetNormal(int index) 169 { 170 Point2D temp; 171 if(index >= 0 && index < _num) 172 { 173 temp = norms[index]; 174 } 175 return temp; 176 } 177 178 void ComputeNormals() 179 { 180 for(int i = 0; i < _num; ++i) 181 { 182 Line2D now = GetLine(i); 183 Line2D next; 184 if(i == _num - 1) 185 next = GetLine(0); 186 else 187 next = GetLine(i + 1); 188 189 Point2D v = now.GetVector(); 190 Point2D vn = next.GetVector(); 191 Point2D norm; 192 if(v._x != 0) 193 { 194 norm._y = 1; 195 norm._x = (-v._y) / v._x; 196 } 197 else//x and y couldn‘t be zero at same time 198 { 199 norm._x = 1; 200 norm._y = (-v._x) / v._y; 201 } 202 203 if(norm * vn > 0) 204 norm.InverseDir(); 205 norms[i] = norm; 206 } 207 } 208 209 const Point2D& GetPoint(int index) 210 { 211 if(index >= 0 && index <= _num) 212 return points[index]; 213 return Point2D(); 214 } 215 }; 216 217 /* 218 Global Varibles 219 */ 220 const int SCREEN_WIDTH = 800; 221 const int SCREEN_HEIGHT = 600; 222 Point2D g_Start; 223 Point2D g_End; 224 Line2D src; 225 Line2D dest; 226 bool acc; 227 bool buildpoly = true; 228 Polygon g_Poly; 229 int g_Count; 230 std::vector<Point2D> g_V; 231 232 int Cyrus_Beck(Line2D& src, Line2D& dest, Polygon& poly) 233 { 234 float tin = 0.0f, tout = 1.0f; 235 Point2D&& vec = src.GetVector(); 236 237 for(int i = 0; i < poly._num; ++i) 238 { 239 Line2D&& line = poly.GetLine(i); 240 Point2D&& norm = poly.GetNormal(i); 241 float nc = vec * norm; 242 if(nc == 0) 243 continue; 244 else 245 { 246 float hit = (line._start - src._start) * norm / nc; 247 if(nc > 0)//out 248 tout = min(tout, hit); 249 else 250 tin = max(tin, hit); 251 } 252 } 253 254 if(tin <= tout) 255 { 256 dest._start = src._start + vec * tin; 257 dest._end = src._start + vec * tout; 258 } 259 260 return tin > tout; 261 } 262 263 void myInit() 264 { 265 /* 266 Output Info 267 */ 268 std::vector<Point2D> v; 269 v.emplace_back(); 270 g_Count = 0; 271 acc = false; 272 273 glClearColor((float)0x66 / 0x100, (float)0xcc / 0x100, 1.0, 0.0); 274 glColor3f(0.0f, 0.0f, 0.0f);//Map Color Black 275 glPointSize(1.0); 276 glMatrixMode(GL_PROJECTION); 277 278 glLoadIdentity(); 279 gluOrtho2D(0.0, (GLdouble)SCREEN_WIDTH, (GLdouble)SCREEN_HEIGHT, 0.0); 280 glViewport(0.0, SCREEN_WIDTH, 0.0, SCREEN_HEIGHT); 281 } 282 283 void myMouse(int button, int state, int x, int y) 284 { 285 if(buildpoly) 286 { 287 if(button == GLUT_RIGHT_BUTTON && state == GLUT_DOWN) 288 { 289 //build over 290 g_Poly.Set(g_V); 291 g_V.clear(); 292 buildpoly = false; 293 cout << "Build Poly Over."; 294 glutPostRedisplay(); 295 } 296 if(button == GLUT_LEFT_BUTTON && state == GLUT_DOWN) 297 { 298 g_V.emplace_back(x, y); 299 cout << "Add Point: (" << x << ", " << y << ").\n"; 300 glutPostRedisplay(); 301 } 302 return; 303 } 304 305 if(button == GLUT_RIGHT_BUTTON && state == GLUT_DOWN) 306 { 307 buildpoly = true; 308 g_Count = 0; 309 glutPostRedisplay(); 310 return; 311 } 312 313 if(button != GLUT_LEFT_BUTTON || state != GLUT_DOWN) 314 return; 315 316 cout << "MyMouse Called with " << x << ", " << y << endl; 317 switch(g_Count) 318 { 319 case 0: 320 { 321 ++g_Count; 322 g_Start._x = x; 323 g_Start._y = y; 324 src._start = g_Start; 325 }break; 326 case 1: 327 { 328 ++g_Count; 329 g_End._x = x; 330 g_End._y = y; 331 src._end = g_End; 332 acc = !Cyrus_Beck(src, dest, g_Poly); 333 if(!acc) 334 { 335 cout << "Refused.\n"; 336 } 337 else 338 cout << "Accept.\n"; 339 340 glutPostRedisplay(); 341 }break; 342 case 2: 343 { 344 g_Start._x = x; 345 g_Start._y = y; 346 src._start = g_Start; 347 g_Count = 1; 348 }break; 349 } 350 } 351 352 void myDisplay() 353 { 354 glClear(GL_COLOR_BUFFER_BIT); 355 356 Point2D temp; 357 if(buildpoly) 358 { 359 glColor3f(0.0f, 0.0f, 0.0f);//Poly 360 glPointSize(3.0); 361 glBegin(GL_LINE_STRIP); 362 363 for(int i = 0; i < g_V.size(); ++i) 364 glVertex2d(g_V[i]._x, g_V[i]._y); 365 366 glEnd(); 367 } 368 else 369 { 370 glColor3f(0.0f, 0.0f, 0.0f);//Poly 371 glPointSize(3.0); 372 glBegin(GL_LINE_STRIP); 373 374 for(int i = 0; i < g_Poly._num; ++i) 375 { 376 temp = g_Poly.GetPoint(i); 377 glVertex2d(temp._x, temp._y); 378 } 379 temp = g_Poly.GetPoint(0); 380 glVertex2d(temp._x, temp._y); 381 382 glEnd(); 383 384 if(g_Count == 2) 385 { 386 //Draw Line 387 glColor3f(1.0f, 0.0f, 0.0f);//Normal Line, Red 388 glPointSize(2.0); 389 glBegin(GL_LINES); 390 glVertex2d(src._start._x, src._start._y); 391 glVertex2d(src._end._x, src._end._y); 392 cout << "\nDraw Line\n"; 393 if(acc) 394 { 395 //Draw Cutted Line 396 glColor3f(0.0f, 1.0f, 0.0f);//Normal Line, Green 397 glPointSize(3.0); 398 glVertex2d(dest._start._x, dest._start._y); 399 glVertex2d(dest._end._x, dest._end._y); 400 cout << "\nDraw CutLine\n"; 401 } 402 glEnd(); 403 } 404 } 405 406 407 408 //glutSwapBuffers(); 409 glFlush(); 410 //cout << "Render Over\n"; 411 } 412 413 int main(int argc, char* argv[]) 414 { 415 glutInit(&argc, argv); 416 //glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB); 417 glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB); 418 glutInitWindowSize(SCREEN_WIDTH, SCREEN_HEIGHT); 419 glutInitWindowPosition(0, 0); 420 glutCreateWindow("Cyrus_Beck"); 421 glutDisplayFunc(myDisplay); 422 glutMouseFunc(myMouse); 423 424 myInit(); 425 glutMainLoop(); 426 427 return 0; 428 }
数据结构新增加了一个Polygon,里面有两个Point2D数组,分别是多边形的顶点以及法向量。结构中的ComputeNormals计算出法向量。
算法集中在Cyrus_Beck函数中,该函数接收一条线段以及一个多边形,返回裁剪后的线段,并返回是否有效。其实这个函数看起来很简单,只有短短30行。不过涉及到了一些向量知识,还必须提前计算出法向量。所以还是比Cohen_Sutherland复杂一些。
代码剩下部分则是为了用OpenGL实践Cyrus_Sutherland算法的效果。
程序运行后,先用鼠标左键选取一系列的点构建一个多边形,当然必须是凸多边形,不然算法会有问题。然后鼠标右键完成构建。接下来就是不断的用鼠标左键选取线段的起点和终点进行裁剪了。
运行效果如下:
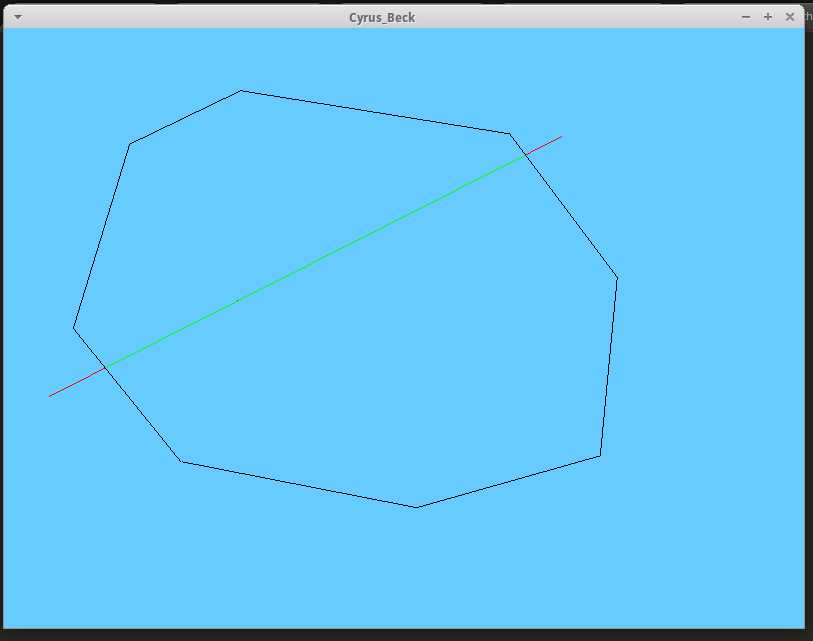
此外,还有几种裁剪算法:

我只尝试实现了前两种,后两种很没有接触,以后有机会应该会尝试一下。
标签:
原文地址:http://www.cnblogs.com/o--o/p/5774433.html