lanczos算法及C++实现（二）实对称阵奇异值分解的QR算法

时间：2016-08-19 06:12:42 阅读：548 评论：0 收藏：0 [点我收藏+]

标签：

本文属作者原创，转载请注明出处：

http://www.cnblogs.com/qxred/p/qralgorithm.html

http://people.inf.ethz.ch/arbenz/ewp/Lnotes/chapter4.pdf

1. 基本的QR算法

我们先讨论一般对阵矩阵的QR算法，再讨论对称三对角阵的QR算法

给定一个实对称阵X,假设其特征值分解为X=PSP‘，其中P对正交阵，S是对角阵。求P,S的QR算法如下，其中 $技术分享$ 为正交阵， $技术分享$ 为上三角阵：

$技术分享$
for k=1,2, ...
$技术分享$ （QR分解）
$技术分享$
endfor
$技术分享$
将 $技术分享$ 的非对角线元素置0即得S

用matlab代码表示，即

function [P,S]=qreigen
A=rand(10);
A=A+A‘      %Symmetry real matrix, otherwise P‘AP is a block upper triangle matrix
m=size(A,1);
P=eye(m);
for i=1:1000
        [Q,R]=qr(A); %QR factorization
        A=R*Q;
        P=P*Q;
end
S=diag(diag(R));
end

这个算法很简单，每次迭代做一个QR分解和一个矩阵乘法。最基本的，我们用施密特正交化进行QR分解，这在上一篇lanczos算法及C++实现（一）框架及简单实现中使用。附录A讨论了QR方法和幂迭代方法的关系。

值得注意的是，如果矩阵X不是对称阵，这个方法往往不能收敛到一个上三角阵，而是一个块状上三角阵。（我一开始不知道，还以为程序错误，调了半天）有兴趣的同学可以试一下如下代码：

function [P,A]=qreigen
A=rand(10); %not symmetry
m=size(A,1);
P=eye(m);
for i=1:1000
        [Q,R]=qr(A); %QR factorization
        A=R*Q;
        P=P*Q;
end
% A is block upper triangle matrix, not upper triangle
A
end

运行结果如下：

A =

    4.7120   -0.6211    0.4352   -0.0450   -0.1297    0.5700   -0.3769    0.4790   -0.0754    0.2798
         0    0.0273    0.8587   -0.2188   -0.0095   -0.1913   -0.3785   -0.2142   -0.0565   -0.1236
         0   -0.9150    0.3761   -0.0914    0.0217   -0.1527    0.0317    0.4235    0.4612   -0.3284
         0   -0.0000    0.0000   -0.7400   -0.0686    0.2954    0.1561   -0.1755    0.1879   -0.2237
         0   -0.0000    0.0000   -0.0000    0.4096   -0.5238   -0.0330    0.1636    0.3090   -0.4849
         0    0.0000    0.0000   -0.0000    0.2002    0.7429    0.2064   -0.4820   -0.2602   -0.2005
         0         0         0    0.0000   -0.0000   -0.0000   -0.3812   -0.1792   -0.0188   -0.4469
         0         0         0    0.0000   -0.0000    0.0000    0.4117   -0.1513    0.1134   -0.2247
         0         0         0    0.0000   -0.0000    0.0000    0.0000    0.0000   -0.3465    0.0887
         0         0         0         0         0         0   -0.0000   -0.0000   -0.0000    0.1833

2. 快速QR算法

施密特正交法每次需要O(n^3)的计算，很慢。所以通常不用这个方法。一般来说，我们采用如下QR算法，该算法分成两步：

1、利用Householder变换 (如果你对Householder变换不了解，请见附录B)，将X正交变换为上海森伯格阵(Upper Hessenburg Matrix)，复杂度O(n^3)。

2、在每次迭代中，利用Givens变换 (如果你对Givens变换不了解，请见附录C)，求得上海森伯格阵的QR分解，复杂度O(n^2)。

这样只有在迭代之前需要O(n^3)的预处理，而每次迭代只要平方复杂度，因此比施密特正交法快很多。

2.1 矩阵的上海森伯格化 Hessenburg Reduction

在这一步，对一个方阵X(不要求对称)，我们要求一个正交变换P，使得PXP‘为上海森伯格矩阵，即低于对角线下一行的所有元素为0：
$技术分享$

如何求得这样的P呢？基本思想如下，将矩阵X分成4块：

$技术分享$

然后用Householder变换，将左下的一列变为只有一个非零元素：

$技术分享$
其中 $技术分享$ 是一个正交矩阵，

$技术分享$ ，

$技术分享$ 是一个除第i个分量为1以外，其他分量为0的向量。P1的具体求法，参见附录B

这样我们有

$技术分享$

类似的，我们可以构造 $技术分享$ 等共n-1个矩阵，使得X正交相似于一个上海森伯格矩阵。

值得一提的是，如果X是一个对称阵，那么根据对称性，X正交相似于一个三对角阵。

2.2 上海森伯矩阵的QR分解

首先，如果H是一个上海森伯格阵，其QR分解为H=QR，那么RQ也是一个上海森伯格阵。证明省略。

这就是说，如果我们有一个对海森伯格阵的快速QR算法，那么在每次迭代中我们可以反复使用该算法。我们采用Givens变换来进行QR分解。对于n阶上海森伯格阵H,从上到下对每相邻的两行使用Given变换，每次变换都消去对角线下方的一个元素。共n-1次变换。由于Givens变换是正交变换，那么这n-1次变换的乘积也是正交变换，变换后， $技术分享$ 变成了上三角阵。其中 $技术分享$ 是第i次Givens行变换的矩阵表示。根据QR算法，我们需要求RQ。因此在对H进行n-1次行变换后，再从左到右对每相邻的两列使用对应的Given变换的逆变换，同样一共也是n-1次变换： $技术分享$ ，这样我们就完成了一次迭代。这个过程可以用下图表示：

QR分解过程, $技术分享$ ，其中红框代表当前需要考虑的H中的元素，这些元素将被更新。注意每次Givens变换将一个对角线下的元素变成0.

技术分享

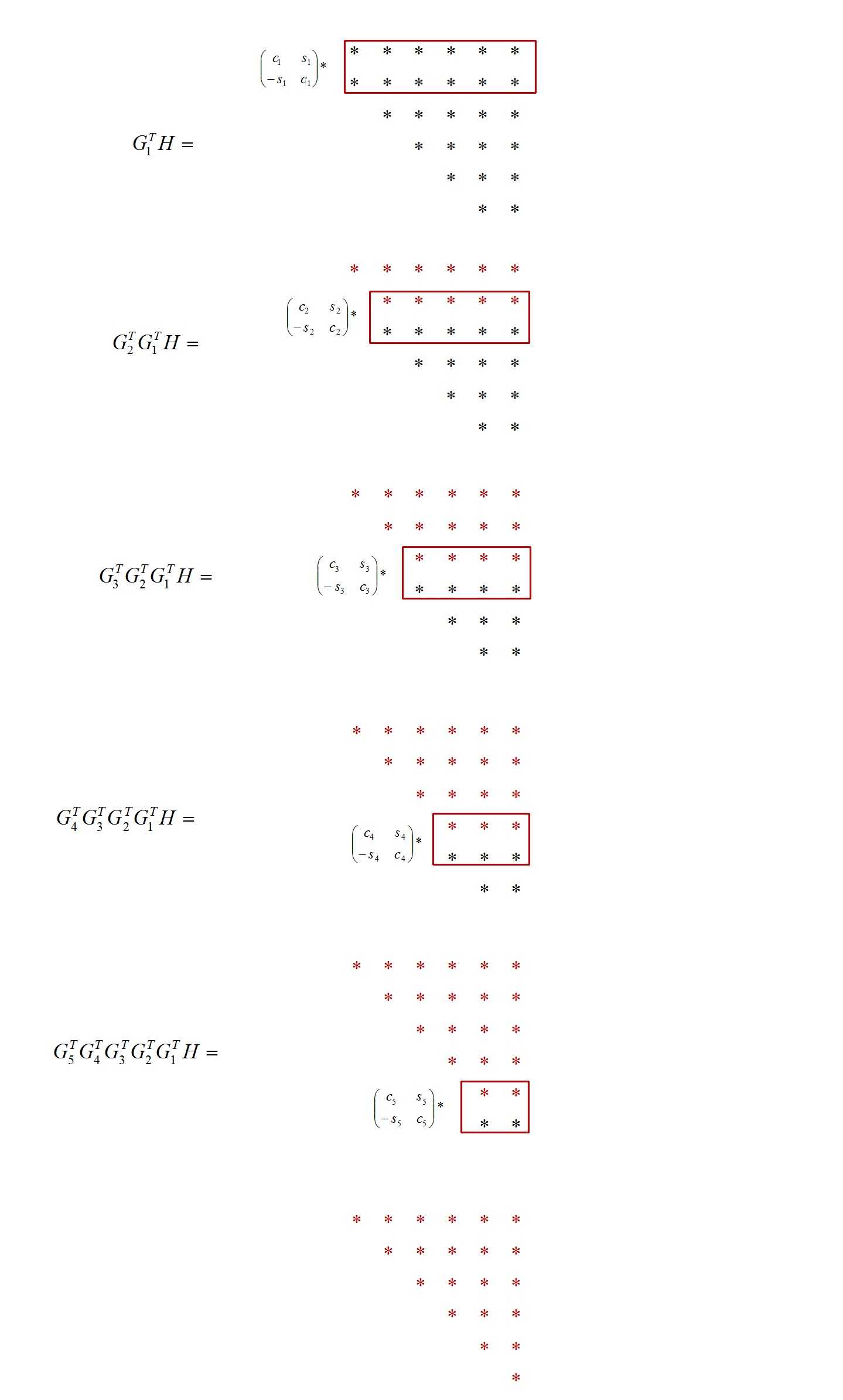
而R*Q的过程如下：

技术分享

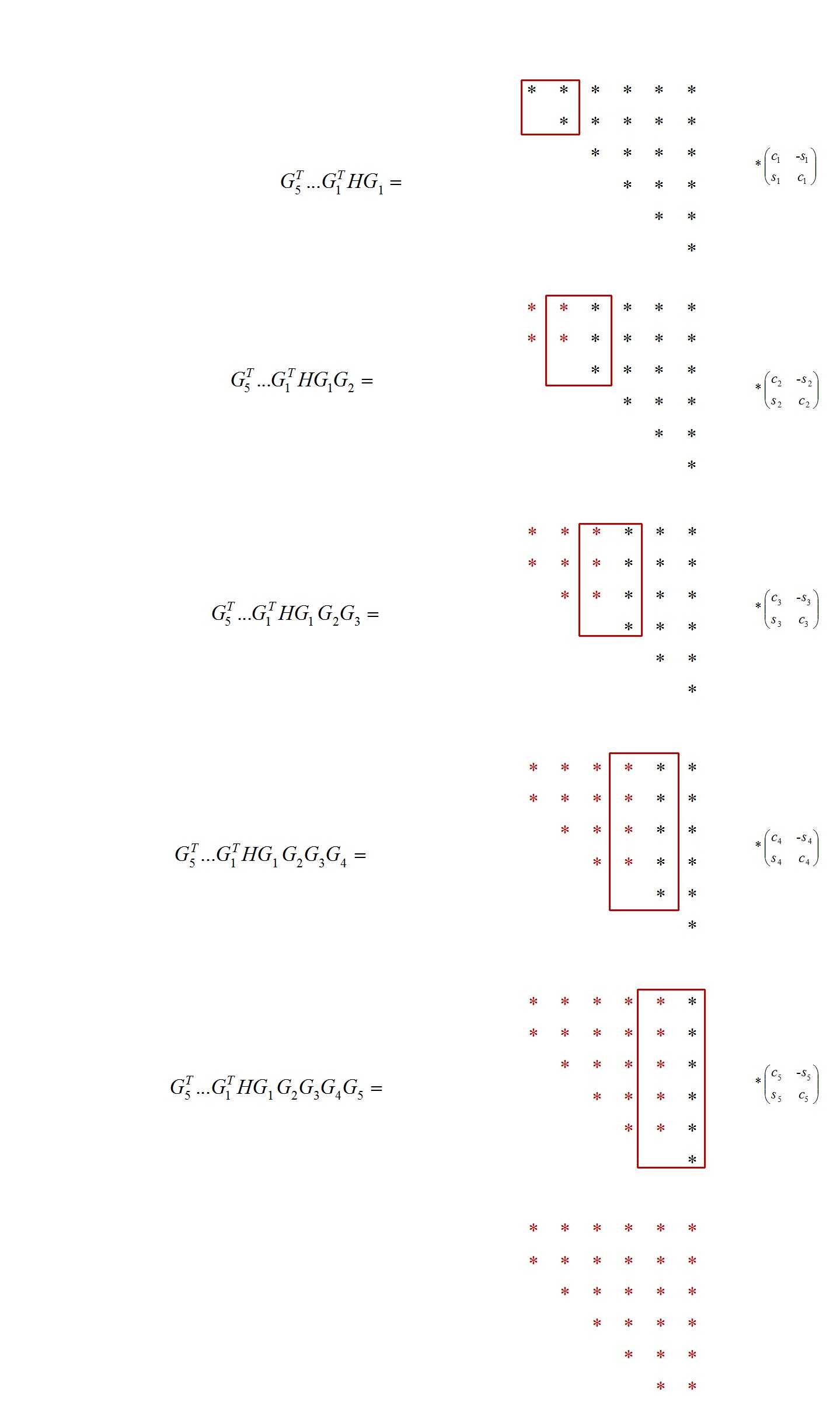
其中

$技术分享$

将这个过程中所有产生的G乘起来就得到了H的特征向量。我们可以看到，每次迭代只需要O(n^2)的计算量，比施密特正交化快多了。

2.3 三对角阵的特征值分解

在lanczos方法中，我们得到的是一个对称三对角阵，是上海森伯格阵的特例。因此可以用上面所述方法计算特征值。值得注意的是，这里可以利用三对角阵的特性加速计算，在求第一个行变换G‘1H的时候，可以只考虑H左上的2*3的小阵，而不是整个前两行。而接下来的每次行变换也只需考虑H的2*3的子阵。在列变换中，每次只需考虑H的3*2的子阵即可。这样一次QR迭代的复杂度只有O(n)了。

2.4 通过平移(shifts)和deflation加速上海森伯格矩阵的特征值分解

由于QR算法的收敛速度取决于特征值之间的差异，差别越大，QR收敛越快。这和幂迭代算法是一致的。那么怎么加快特征值之间的差异呢？通常的做法就是平移。

假设H有两个特征值 $技术分享$ ，那么QR迭代的速度为 $技术分享$ 。假如 $技术分享$ 满足 $技术分享$ ，那么矩阵 $技术分享$ 和H有相同的特征向量，其特征值为 $技术分享$ ，而求H^*的特征向量会很快，其收敛速度为 $技术分享$

基于这样的观察，在求海森伯格矩阵的特征值时，每次迭代我们进行如下QR分解

$技术分享$ （QR分解）
$技术分享$
显然，这样的QR分解不改变H的特征向量，但是如果选取合适的 $技术分享$ 收敛速度要快很多。特别地，如果 $技术分享$ 恰好取到某个的特征值时，那么一次迭代即可就可确定该特征值。见文献https://www.math.kth.se/na/SF2524/matber15/qrmethod.pdf中的lemma 2.3.2。事实上我们没那么幸运，但可以用每次迭代中，H对角线上的元素可以看作是特征值的估计。所以每次计算完RQ后，取对角线上固定某个位置的元素（比如始终取第1个）作为 $技术分享$ 。但如果矩阵存在一对特征值互为相反数，那么这种方法不能收敛。比如矩阵 $技术分享$ ，因此更好的做法是Wilkinson shift，取H对角线上的2*2的方阵的特征值作为 $技术分享$ 。此外对复矩阵还有双位移方法(Double shift)，这里不作详细的讨论，有兴趣的读者可以参考http://people.inf.ethz.ch/arbenz/ewp/Lnotes/chapter4.pdf

那么这样只能加速计算某个特征值，比如始终取对角线上的最后一个则加快了求解最小特征值的速度。如何加速求解其他特征值的速度呢？这里就用到了deflation。

抱歉我不知道怎么翻译这个词deflation，因此就用英文了。

Deflation是指在迭代过程中，如果对角线上某个位置的下一行几乎为0的时候，说明该位置上的值很接近于特征值了，此时将改位置所对应的行和列从矩阵中刨去，对剩下的矩阵进行计算。

一般的步骤如下，取对角线最右下的元素做deflation，直到该元素左边的元素几乎为0时，这时最小特征值已经求出，将最后一行一列去掉，对剩下的矩阵继续计算。如此反复，deflate n-1次之后，所有特征值全部求出。

2.5 QR算法的C++实现

最后，附上我的QR算法的C++实现。这个算法实现了这篇文章中的所有内容，包括实对称阵到上海森伯格阵的转化（hessenburgReduction函数），上海森伯格阵特征值分解的QR算法(QRHessenberg函数)，三对角阵的特征值分解的QR算法(QRTridiagonal函数)，每个QR算法中都用了shift和deflation加速，采用的是Wilkinson shift。在Lanczos算法中，只有QRTridiagonal函数被调用。当然如果不用lanczos方法三对角化，也可以通过hessenburgReduction函数和QRHessenberg函数来进行QR迭代求解特征值分解。具体代码参见附录 D，有三个文件svds.h, svds.cpp, main.cpp。编译时用命令g++ main.cpp svds.cpp

附录

附录 A QR算法等价于并行幂迭代算法(Simultaneous Iteration)

QR算法实际上等价于并行幂迭代算法 (Simultaneous Iteration)。在幂迭代中，如果我们用一组线性独立的向量而不是一个向量与X反复相乘，则最终得到的将是一组线性独立的向量，对其正交化后，可以得到X的特征向量。但实际上由于幂迭代的性质，这些向量快速的收敛到主特征向量，而其他的特征向量被快速丢弃。为了保留较小特征向量的成分，每次与X相乘后，都做一次正交化，那么这样最终这些向量将收敛到X的不同的特征向量。如果一开始选取的一组向量是单位阵，那么这种并行的幂迭代算法，实际上就是QR算法。为什么这么说呢？我们可以看到，第一迭代，这组向量相乘X，得到X，然后正交化。而正交化实际上就是QR分解： $技术分享$ ，接着第二次迭代，我们用X乘 $技术分享$ 并正交化： $技术分享$ ，如此我们得到
$技术分享$
$技术分享$
$技术分享$
...
比较一下QR算法 $技术分享$
$技术分享$
$技术分享$
...
用数学归纳法可以证明QR算法中的 $技术分享$ 和并行幂迭代中的 $技术分享$ 相同。因为当k=1时，显然成立，当k=2时并行幂迭代中 $技术分享$ 而QR算法中 $技术分享$ 由于 $技术分享$ 是正交阵，一个矩阵在进行行正交变换（左乘正交阵）后，其QR分解中的R不变。因此两者的 $技术分享$ 相同
以此类推。可以证明两个算法中所有的 $技术分享$ 相同
然后，我们可以得到在并行幂迭代中，
$技术分享$
而QR算法中
$技术分享$
于是，可以得到两个算法中 $技术分享$ 的联系：
$技术分享$

附录 B Householder变换

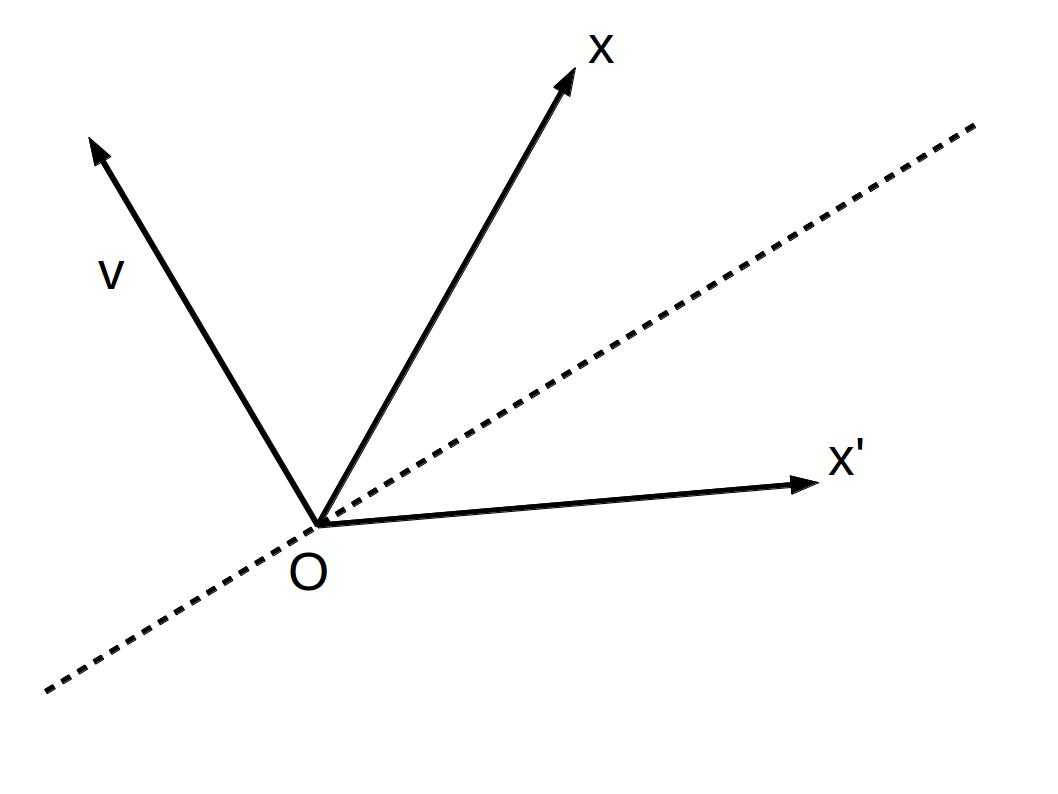
又名Householder Reflections，顾名思义，是一种镜像变换。如图，假设给定一个点x和一个过原点的平面（虚线）,平面用一个垂直于它的单位向量v表示，那么对x的Householder变换就是求x关于平面v的镜像点x‘。现在我们来看怎么计算x‘

首先0指向x的向量在向量v上的投影为 $技术分享$ ，在平面v上的投影为 $技术分享$ 。所以其镜像点x‘的坐标为 $技术分享$

这里矩阵 $技术分享$ 就是一个householder矩阵，是一个对称的正交矩阵，有两个特征值，1和-1

现在我们考虑如何利用householder变换将一个向量变x成只有一个非0元素的向量,如下图所示

技术分享

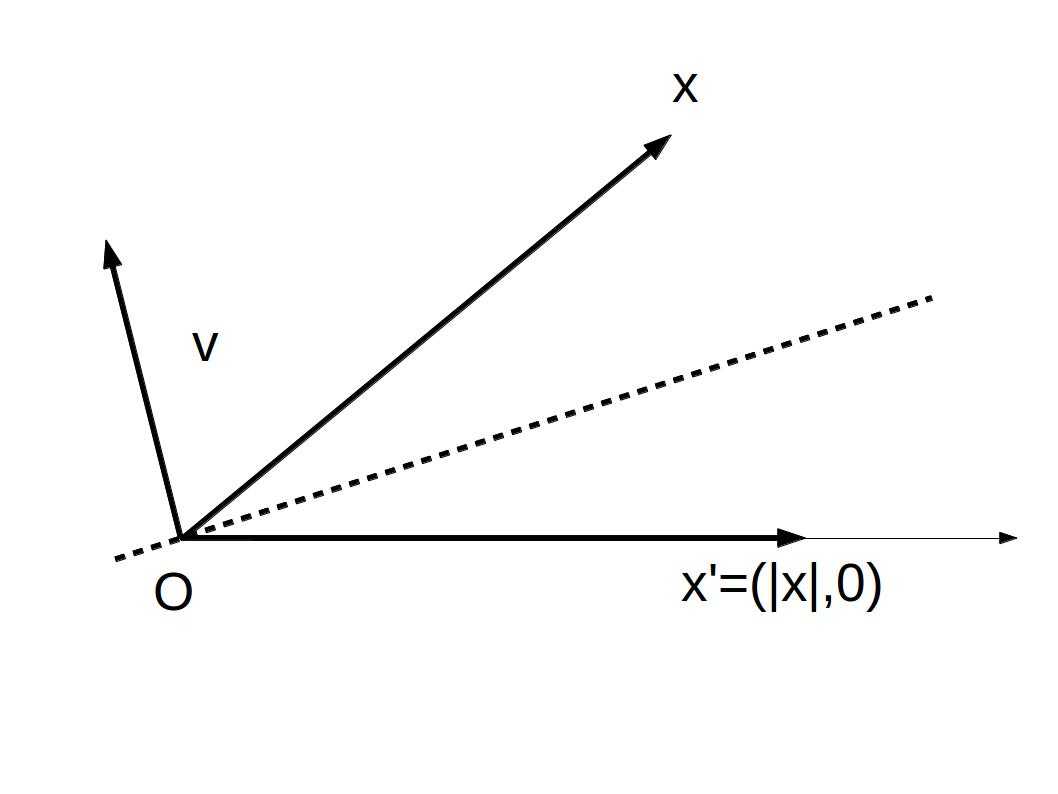
关键就是求那个平面，即v向量。由图可得出x-x‘平行于v，因此我们有

$技术分享$

其中

$技术分享$

附录 C Givens变换

又名Givens旋转，顾名思义，是对一个向量进行旋转变换，不改变向量的长度，因此是一个正交变换，其逆变换就是反方向旋转回去。

技术分享

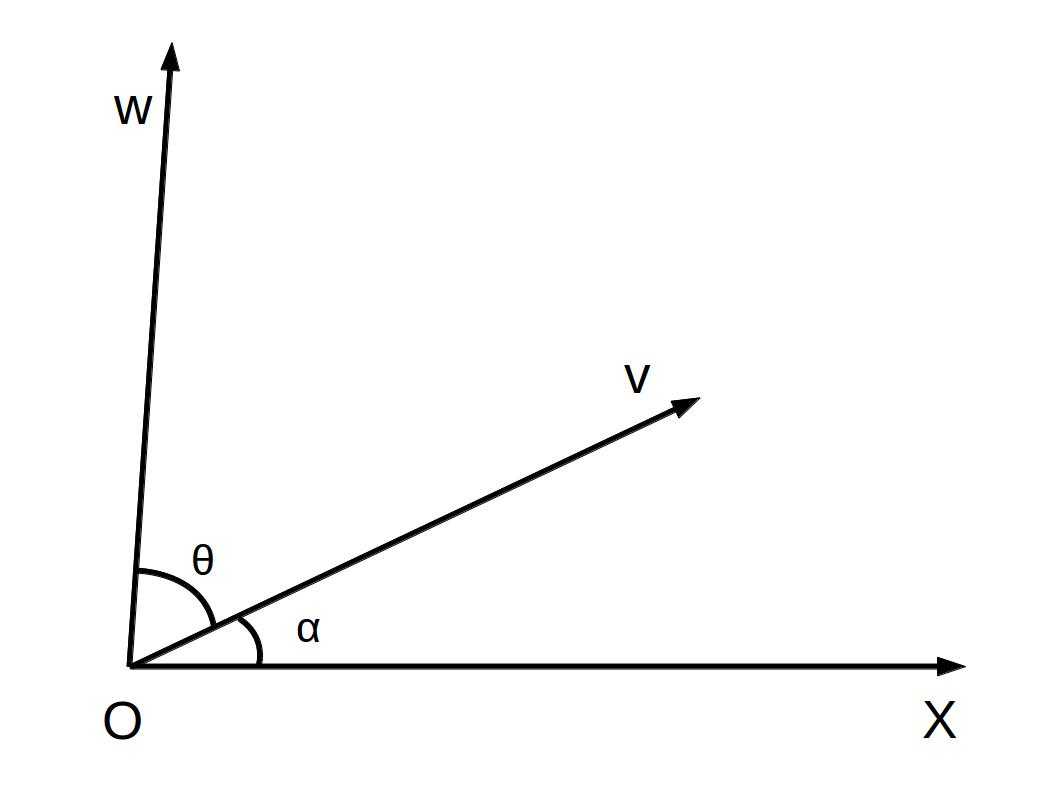
如图所示，我们考虑一个二维向量 $技术分享$ ，将它逆时针旋转 $技术分享$ 角度后，求所得到的坐标。

这里我们可以将向量重新表示为 $技术分享$ ，其中 $技术分享$ 是向量v与x坐标轴的夹角。

这样变换后的坐标为

$技术分享$

其中 $技术分享$ 为Givens变换矩阵，是一个正交阵，其逆阵为

$技术分享$

附录 D: QR分解的C++代码

svds.h

#ifndef SVDS_H
#define SVDS_H
#include <vector>
using namespace std;
class Cell{
public:
    unsigned int row;
    unsigned int col;
    double value;
    Cell():row(0),col(0),value(0){};
    Cell(int r, int c, double v):row(r),col(c),value(v){};
};
class SparseMatrix{
public:
    unsigned int rows;
    unsigned int cols;
    vector<Cell> cells;

    int cellID;

    //read data sequentially, especially when loading large matrix from the disk.
    void moveFirst(){
        cellID=0;
    }
    bool hasNext(){
        return cellID<cells.size();
    }
    Cell next(){
        return cells[cellID++];
    }
};

void svds(SparseMatrix &A, int r, vector<vector<double> > &U, vector<double> &s, vector<vector<double> > &V);
//decompose A = U * diag(s) *V‘
//where A is a m*n matrix
//U is a m*r column orthogonal matrix
//s is a length r vector
//V is a n*r column orthogonal matrix

void print(vector<vector<double> > &X);
void hessenbergReduction(vector<vector<double> > &A, vector<vector<double> > &U);
void QRHessenbergBasic(vector<vector<double> > &A, vector<vector<double> > &Q);
void QRbasic(vector<vector<double> > &T, vector<vector<double> > &W);
void transpose(vector<vector<double> > &A, vector<vector<double> > &T);
void multiply(vector<vector<double> > &A, vector<vector<double> > &B, vector<vector<double> > &C);
void QRHessenberg(vector<vector<double> > &A, vector<vector<double> > &Q);
void QRTridiagonal(vector<vector<double> > &A, vector<vector<double> > &Q);
#endif

svds.cpp

#include <iostream>
#include <fstream>
#include <vector>
#include <string>
#include <cmath>
#include <climits>
#include <cstdlib>
#include <algorithm>
#include<iomanip>
#include "svds.h"
using namespace std;
const double EPS=1e-15;
void print(vector<vector<double> > &X){
    cout.precision(6);
    cout.setf(ios::fixed);
    for(int i=0;i<X.size();i++){
        for(int j=0;j<X[i].size();j++)
            cout<<X[i][j]<<‘ ‘;
        cout<<endl;
    }
    cout<<endl;
}

void transpose(vector<vector<double> > &A, vector<vector<double> > &T){
    if(A.empty()||A[0].empty()) return;
    int m=A.size();
    int n=A[0].size();
    T.clear();
    T.resize(n,vector<double>(m,0));
    for(int i=0;i<m;i++)
        for(int j=0;j<n;j++)
            T[j][i]=A[i][j];
}
void transpose(vector<vector<double> > &A){
    int m=A.size();
    for(int i=0;i<m;i++)
        for(int j=i+1;j<m;j++)
            swap(A[i][j],A[j][i]);
}

void randUnitVector(int n, vector<double> &v){
    srand(time(NULL));
    v.clear();v.resize(n);
    while(true){
        double r=0;
        for(int i=0;i<n;i++){
            v[i]=rand()*1.0/RAND_MAX-0.5;
            r+=v[i]*v[i];
        }
        r=sqrt(r);
        if(r>EPS){
            for(int i=0;i<n;i++)
                v[i]/=r;
            break;
        }
    }
}
void multiply(vector<vector<double> > &A, vector<vector<double> > &B, vector<vector<double> > &C){
    //C=A*B
    C.clear();
    if(A.empty() || A[0].empty() || B.empty() || B[0].empty()) return ;
    C.resize(A.size(),vector<double>(B[0].size(),0));
    for(int i=0;i<A.size();i++){
        for(int j=0;j<B[0].size();j++){
            C[i][j]=0;
            for(int k=0;k<A[0].size();k++){
                C[i][j]+=A[i][k]*B[k][j];
            }
        }
    }
}

void multiply(const vector<vector<double> > &X, const vector<double> & v, vector<double> & res){
    res.clear();
    if(X.empty() || v.empty()) return;
    int m=X[0].size();
    res.resize(m,0);
    for(int i=0;i<m;i++){
        for(int j=0;X[i].size();j++){
            res[i]+=X[i][j]*v[j];
        }
    }
}
double dotProduct(const vector<double> & a, const vector<double> & b){
    double res=0;
    for(int i=0;i<a.size();i++)
        res+=a[i]*b[i];
    return res;
}


void rightMultiply(SparseMatrix &A, const vector<double> & v, vector<double> & res){
    //res= A*A‘*v
    int m=A.rows;
    int n=A.cols;
    res.clear();
    res.resize(m,0);
    vector<double> w(n,0);
    A.moveFirst();
    while(A.hasNext()){
        Cell c=A.next();
        w[c.col]+=c.value*v[c.row];
    }
    A.moveFirst();
    while(A.hasNext()){
        Cell c=A.next();
        res[c.row]+=c.value*w[c.col];
    }
}
void leftMultiply(SparseMatrix &A, const vector<double> & v, vector<double> & res){
    //res= A‘*A*v
    int m=A.rows;
    int n=A.cols;
    res.clear();
    res.resize(n,0);
    vector<double> w(m,0);
    A.moveFirst();
    while(A.hasNext()){
        Cell c=A.next();
        w[c.row]+=c.value*v[c.col];
    }
    A.moveFirst();
    while(A.hasNext()){
        Cell c=A.next();
        res[c.col]+=c.value*w[c.row];
    }
}

void rightMultiply(const vector<vector<double> > & B,SparseMatrix &A, vector<vector<double> > & C){
    //C= B‘*A
    int m=B[0].size();
    int k=B.size();
    int n=A.cols;
    for(int i=0;i<C.size();i++) fill(C[i].begin(),C[i].end(),0);
    A.moveFirst();
    while(A.hasNext()){
        Cell c=A.next();
        for(int i=0;i<m;i++){
            C[c.col][i]+=c.value*B[c.row][i];
        }
    }
}
void leftMultiply(const vector<vector<double> > & B,SparseMatrix &A, vector<vector<double> > & C){
    //C <- A B
    int r=B[0].size();
    int n=B.size();
    int m=A.rows;
    C.clear();
    C.resize(m,vector<double>(r,0));
    A.moveFirst();
    while(A.hasNext()){
        Cell c=A.next();
        for(int i=0;i<r;i++){
            C[c.row][i]+=c.value*B[c.col][i];
        }
    }
}


double norm(const vector<double> &v){
    double r=0;
    for(int i=0;i<v.size();i++)
        r+=v[i]*v[i];
    return sqrt(r);
}

double normalize(vector<double> &v){
    double r=0;
    for(int i=0;i<v.size();i++)
        r+=v[i]*v[i];
    r=sqrt(r);
    if(r>EPS){
        for(int i=0;i<v.size();i++)
            v[i]/=r;
    }
    return r;
}

void multiply(vector<double> &v, double d){
    for(int i=0;i<v.size();i++)
        v[i]*=d;
}
void hessenbergReduction(vector<vector<double> > &A, vector<vector<double> > &U){
    //A: m*m matrix
    //Reduction A to Hessenberg form: H=U‘AU (A=UHU‘), H overwrite A to save memory
    int m=A.size();
    vector<double> v(m);
    U.clear();
    U.resize(m,vector<double>(m,0));
    for(int i=0;i<m;i++)
        U[i][i]=1;
    for(int i=1;i<m;i++){
        fill(v.begin(),v.end(),0);
        for(int j=i;j<m;j++)
            v[j]=A[j][i-1];
        v[i]-=norm(v);
        normalize(v);    //P=I-2*v*v‘
        //A=PAP
        //1. PA
        for(int j=i-1;j<m;j++){
            double d=0;
            for(int k=i;k<m;k++)
                d+=A[k][j]*v[k];
            for(int k=i;k<m;k++)
                A[k][j]-=d*2*v[k];
        }
        //2. AP
        for(int j=0;j<m;j++){//row j
            double d=0;
            for(int k=i;k<m;k++)
                d+=A[j][k]*v[k];
            for(int k=i;k<m;k++)
                A[j][k]-=d*2*v[k];
        }

        //U=U*P
        for(int j=0;j<m;j++){
            double d=0;
            for(int k=i;k<m;k++)
                d+=U[j][k]*v[k];
            for(int k=i;k<m;k++)
                U[j][k]-=d*2*v[k];
        }
    }
}

void givensRotation(double a, double b, double &c, double &s){
    if(fabs(b)<EPS){
        c=1;s=0;
    }else{
        if(fabs(b)>fabs(a)){
            double r=a/b;
            s=1/sqrt(1+r*r);
            c=s*r;
        }else{
            double r=b/a;
            c=1/sqrt(1+r*r);
            s=c*r;
        }
    }
}

void QRTridiagonal(vector<vector<double> > &A, vector<vector<double> > &Q){
    //input: A m*m symmetry tridiagonal matrix
    //output: Upper triangular R, and orthogonal Q, such that A=QRQ‘
    int n=A.size();
    Q.clear();
    Q.resize(n,vector<double>(n,0));
    vector<double> cs(n-1,0);
    vector<double> ss(n-1,0);
    for(int i=0;i<n;i++) Q[i][i]=1;
    for(int m=n;m>=2;m--){
        while(1){
            fill(cs.begin(),cs.end(),0);
            fill(ss.begin(),ss.end(),0);
            double delta=(A[m-2][m-2]-A[m-1][m-1])/2;
            double sign=1;
            if(delta<0) sign=-1;
            //Wilkinson shift
            double shift=A[m-1][m-1]-sign*A[m-1][m-2]*A[m-2][m-1]/(fabs(delta)+sqrt(delta*delta+A[m-1][m-2]*A[m-2][m-1]));
            for(int i=0;i<m;i++)
                A[i][i]-=shift;
            for(int i=0;i<m-1;i++){
                double a=A[i][i];
                double b=A[i+1][i];
                givensRotation(a,b,cs[i],ss[i]);
                for(int j=i;j<=i+2 && j<m;j++){
                    a=A[i][j];
                    b=A[i+1][j];
                    A[i][j]=cs[i]*a+ss[i]*b;
                    A[i+1][j]=-ss[i]*a+cs[i]*b;
                }
            }
            
            for(int j=1;j<m;j++){// cols    j-1, j                           c -s
                for(int i=max(0,j-2);i<=j;i++){// rows  0 ... j        [a ,b]     s  c
                    double a=A[i][j-1];
                    double b=A[i][j];
                    A[i][j-1]=cs[j-1]*a+ss[j-1]*b;
                    A[i][j]=-ss[j-1]*a+cs[j-1]*b;
                }
            }
            for(int i=0;i<m;i++)
                A[i][i]+=shift;
            //Q=Q*G1...Gm
            for(int j=1;j<m;j++){
                for(int i=0;i<n;i++){
                    double a=Q[i][j-1];
                    double b=Q[i][j];
                    Q[i][j-1]=cs[j-1]*a+ss[j-1]*b;
                    Q[i][j]=-ss[j-1]*a+cs[j-1]*b;
                }
            }
            if(fabs(A[m-1][m-2])<1e-10)
                break;
        }
    }
}


void QRHessenberg(vector<vector<double> > &A, vector<vector<double> > &Q){
    //input: A m*m square Hessenberg Matrix
    //output: Upper triangular R, and orthogonal Q, such that A=QRQ‘
    int n=A.size();
    Q.clear();
    Q.resize(n,vector<double>(n,0));
    vector<double> cs(n-1,0);
    vector<double> ss(n-1,0);
    for(int i=0;i<n;i++) Q[i][i]=1;
    for(int m=n;m>=2;m--){
        while(1){
            fill(cs.begin(),cs.end(),0);
            fill(ss.begin(),ss.end(),0);
            double delta=(A[m-2][m-2]-A[m-1][m-1])/2;
            double sign=1;
            if(delta<0) sign=-1;
            //Wilkinson shift
            double shift=A[m-1][m-1]-sign*A[m-1][m-2]*A[m-2][m-1]/(fabs(delta)+sqrt(delta*delta+A[m-1][m-2]*A[m-2][m-1]));
            for(int i=0;i<m;i++)
                A[i][i]-=shift;
            for(int i=0;i<m-1;i++){
                double a=A[i][i];
                double b=A[i+1][i];
                givensRotation(a,b,cs[i],ss[i]);
                for(int j=i;j<m;j++){
                    a=A[i][j];
                    b=A[i+1][j];
                    A[i][j]=cs[i]*a+ss[i]*b;
                    A[i+1][j]=-ss[i]*a+cs[i]*b;
                }
            }
            
            for(int j=1;j<m;j++){// cols    j-1, j                           c -s
                for(int i=0;i<=j;i++){// rows  0 ... j        [a ,b]     s  c
                    double a=A[i][j-1];
                    double b=A[i][j];
                    A[i][j-1]=cs[j-1]*a+ss[j-1]*b;
                    A[i][j]=-ss[j-1]*a+cs[j-1]*b;
                }
            }
            for(int i=0;i<m;i++)
                A[i][i]+=shift;
            //Q=Q*G1...Gm
            for(int j=1;j<m;j++){
                for(int i=0;i<n;i++){
                    double a=Q[i][j-1];
                    double b=Q[i][j];
                    Q[i][j-1]=cs[j-1]*a+ss[j-1]*b;
                    Q[i][j]=-ss[j-1]*a+cs[j-1]*b;
                }
            }
            if(fabs(A[m-1][m-2])<1e-10)
                break;
        }
    }
}
void QRHessenbergBasic(vector<vector<double> > &A, vector<vector<double> > &Q){
    //input: A m*m square Hessenberg Matrix
    //output: Upper triangular R such taht A=QRQ‘ for orthogonal matrix Q
    int m=A.size();
    vector<double> cs(m-1,0);
    vector<double> ss(m-1,0);
    double diff=1;
    Q.clear();
    Q.resize(m,vector<double>(m,0));
    for(int i=0;i<m;i++) Q[i][i]=1;
    while(1){
        for(int i=0;i<m-1;i++){
            double a=A[i][i];
            double b=A[i+1][i];
            givensRotation(a,b,cs[i],ss[i]);
            for(int j=i;j<m;j++){
                a=A[i][j];
                b=A[i+1][j];
                A[i][j]=cs[i]*a+ss[i]*b;
                A[i+1][j]=-ss[i]*a+cs[i]*b;
            }
        }
        
        for(int j=1;j<m;j++){// cols    j-1, j                c -s
            for(int i=0;i<=j;i++){// rows  0 ... j        [a ,b]    s  c
                double a=A[i][j-1];
                double b=A[i][j];
                A[i][j-1]=cs[j-1]*a+ss[j-1]*b;
                A[i][j]=-ss[j-1]*a+cs[j-1]*b;
            }
        }
        //Q=Q*G1...Gm
        for(int j=1;j<m;j++){
            for(int i=0;i<m;i++){
                double a=Q[i][j-1];
                double b=Q[i][j];
                Q[i][j-1]=cs[j-1]*a+ss[j-1]*b;
                Q[i][j]=-ss[j-1]*a+cs[j-1]*b;
            }
        }
        diff=0;
        for(int i=0;i+1<m;i++){
            diff+=A[i+1][i]*A[i+1][i];
        }
        diff=sqrt(diff);
        if(diff<1e-10)
            break;
    }
}


void QRFactorization(vector<vector<double> > &A, vector<vector<double> > &Q, vector<vector<double> > &R){
    //A=Q*R
    //A: m*n matrix
    //Q: m*m matrix
    //R: m*n matrix
    int m=A.size();
    int n=A[0].size();
    for(int i=0;i<Q.size();i++)
        fill(Q[i].begin(),Q[i].end(),0);
    for(int i=0;i<R.size();i++)
        fill(R[i].begin(),R[i].end(),0);

    vector<double> q(m);
    vector<double> r(n);
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++)
            q[j]=A[j][i];
        fill(r.begin(),r.end(),0);
        for(int j=0;j<i && j<m;j++){
            r[j]=0;
            for(int k=0;k<q.size();k++)
                r[j]+=Q[k][j]*q[k];
            for(int k=0;k<q.size();k++)
                q[k]-=Q[k][j]*r[j];
        }
        if(i<m){
            r[i]=normalize(q);
            for(int j=0;j<m;j++)
                Q[j][i]=q[j];
        }
        for(int j=0;j<m;j++){
            R[j][i]=r[j];
        }
    }
}


void lanczos(SparseMatrix &A, vector<vector<double> > &P, vector<double> &alpha, vector<double> &beta, unsigned int rank){
    //P‘*A*A‘*P = T = diag(alpha) + diag(beta,1) + diag(beta, -1)
    //P=[p1,p2, ... , pk]
    rank=min(A.cols,min(A.rows,rank));
    vector<double> p;
    unsigned int m=A.rows;
    unsigned int n=A.cols;
    vector<double> prevP(m,0);
    randUnitVector(m,p);
    P.clear();
    P.resize(m,vector<double>(rank,0));
    vector<double> v;
    alpha.clear();alpha.resize(rank);
    beta.clear();beta.resize(rank);
    beta[0]=0;
    for(int i=0;i<rank;i++){
        for(int j=0;j<p.size();j++){
            P[j][i]=p[j];
        }
        rightMultiply(A, p, v);
        alpha[i]=dotProduct(p,v);
        if(i+1<rank){
            for(int j=0;j<m;j++)
                v[j]=v[j]-beta[i]*prevP[j]-alpha[i]*p[j];
            beta[i+1]=norm(v);
            prevP=p;
            for(int j=0;j<m;j++)
                p[j]=v[j]/beta[i+1];
        }
    }
}

void lanczosT(SparseMatrix &A, vector<vector<double> > &P, vector<double> &alpha, vector<double> &beta, unsigned int rank){
    //P‘*A‘*A*P = T = diag(alpha) + diag(beta,1) + diag(beta, -1)
    //P=[p1,p2, ... , pk]
    rank=min(A.cols,min(A.rows,rank));
    vector<double> p;
    unsigned int m=A.rows;
    unsigned int n=A.cols;
    vector<double> prevP(n,0);
    randUnitVector(n,p);
    P.clear();
    P.resize(n,vector<double>(rank,0));
    vector<double> v;
    alpha.clear();alpha.resize(rank);
    beta.clear();beta.resize(rank);
    beta[0]=0;
    for(int i=0;i<rank;i++){
        for(int j=0;j<p.size();j++){
            P[j][i]=p[j];
        }
        leftMultiply(A, p, v);
        alpha[i]=dotProduct(p,v);
        if(i+1<rank){
            for(int j=0;j<n;j++)
                v[j]=v[j]-beta[i]*prevP[j]-alpha[i]*p[j];
            beta[i+1]=norm(v);
            prevP=p;
            for(int j=0;j<n;j++)
                p[j]=v[j]/beta[i+1];
        }
    }
}

void QRbasic(vector<vector<double> > &T, vector<vector<double> > &W){
    int l=T.size();
    W.clear();
    W.resize(l,vector<double>(l,0));
    vector<vector<double> > Q(l,vector<double>(l,0));
    vector<vector<double> > R(l,vector<double>(l,0));
    vector<vector<double> > nextW(l,vector<double>(l,0));
    for(int i=0;i<l;i++)
        W[i][i]=1;
    while(true){
        //T=Q*R
        QRFactorization(T,Q,R);
        //T=R*Q
        multiply(R,Q,T);
    print(T);
        //W=W*Q;
        multiply(W,Q,nextW);
        double diff=0;
        for(int i=0;i<l;i++)
            for(int j=0;j<l;j++)
                diff+=(W[i][j]-nextW[i][j]) * (W[i][j]-nextW[i][j]);
    cout<<diff<<endl;
        W=nextW;
        if(diff<EPS*EPS)
            break;
    }
}
void svds(SparseMatrix &A, int r, vector<vector<double> > &U, vector<double> &s, vector<vector<double> > &V){
    //A=U*diag(s)*V‘
    //A:m*n matrix sparse matrix
    //U:m*r matrix, U[i]=i th left singular vector
    //s:r vector
    //V:n*r matrix, V[i]=i th right singular vector
    int m=A.rows;
    int n=A.cols;
   
    //lanczos: A*A‘=P*T*P‘
    if(m<=n){
        int l=m;
        vector<vector<double> > P(m,vector<double>(l,0));
        vector<double> alpha(l,0);
        vector<double> beta(l,0);
        lanczos(A,P,alpha,beta,l);
        vector<vector<double> > T(l,vector<double>(l,0));
        for(int i=0;i<l;i++){
        T[i][i]=alpha[i];
        if(i)
            T[i-1][i]=T[i][i-1]=beta[i];
        }
        vector<vector<double> > W;
        QRTridiagonal(T,W);
        U.clear();U.resize(m,vector<double>(l));
        multiply(P,W,U);
        for(int i=0;i<U.size();i++)
        U[i].resize(r);
        V.clear();V.resize(n,vector<double>(r));
        rightMultiply(U,A,V);
        s.clear();s.resize(r,0);
        for(int i=0;i<r;i++){
        for(int j=0;j<n;j++)
            s[i]+=V[j][i]*V[j][i];
        s[i]=sqrt(s[i]);
        if(s[i]>EPS){
            for(int j=0;j<n;j++)
            V[j][i]/=s[i];
        }
        }
    }else{
        int l=n;
        vector<vector<double> > P(n,vector<double>(l,0));
        vector<double> alpha(l,0);
        vector<double> beta(l,0);
        lanczosT(A,P,alpha,beta,l);
        vector<vector<double> > T(l,vector<double>(l,0));
        for(int i=0;i<l;i++){
        T[i][i]=alpha[i];
        if(i)
            T[i-1][i]=T[i][i-1]=beta[i];
        }
        vector<vector<double> > W;
        QRTridiagonal(T,W);
        V.clear();V.resize(n,vector<double>(l,0));
        U.clear();U.resize(m,vector<double>(r,0));
        multiply(P,W,V);
        for(int i=0;i<V.size();i++)
        V[i].resize(r);
        leftMultiply(V,A,U);
        s.clear();s.resize(r,0);
        for(int i=0;i<r;i++){
            for(int j=0;j<m;j++)
                s[i]+=U[j][i]*U[j][i];
            s[i]=sqrt(s[i]);
            if(s[i]>EPS){
                for(int j=0;j<m;j++)
                U[j][i]/=s[i];
            }
        }
    }
}

main.cpp

#include "svds.h"
#include <iostream>
#include <cstdlib>
int main(){

    cout.precision(6);
    cout.setf(ios::fixed);
    srand(time(NULL));
    SparseMatrix A;
    A.rows=12;
    A.cols=15;
    int rank=4;
    for(int i=0;i<A.rows;i++){
        for(int j=0;j<A.cols;j++){
            A.cells.push_back(Cell(i,j,rand()*1.0/RAND_MAX-0.5));
        }
    }

    vector<vector<double> > U,V;
    vector<double> s;
    svds(A,rank,U,s,V);

    cout<<"[U,S,V]=svds(A,r)"<<endl;
    cout<<"r = "<<rank<<endl;
    cout<<"A = "<<endl;
    A.moveFirst();
    for(int i=0;i<A.rows;i++){
        for(int j=0;j<A.cols;j++)
            cout<<A.next().value<<‘ ‘;
        cout<<endl;
    }
    cout<<endl<<endl;
    

    cout<<endl<<endl;

    cout<<"U = "<<endl;
    print(U);

    cout<<"s = "<<endl;
    for(int i=0;i<s.size();i++){
        for(int j=0;j<s.size();j++){
            if(i==j)    
                cout<<s[i]<<‘ ‘;
            else
                cout<<0.0<<‘ ‘;
        }
        cout<<endl;
    }
    cout<<endl;
    cout<<endl;
    


    cout<<"V = "<<endl;
    print(V);

    return 0;
}

lanczos算法及C++实现（二）实对称阵奇异值分解的QR算法

标签：

原文地址：http://www.cnblogs.com/qxred/p/qralgorithm.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行