标签:
卷积神经网络(Convolution Neural Network, CNN)在数字图像处理领域取得了巨大的成功,从而掀起了深度学习在自然语言处理领域(Natural Language Processing, NLP)的狂潮。2015年以来,有关深度学习在NLP领域的论文层出不穷。尽管其中必定有很多附庸风雅的水文,但是也存在很多经典的应用型文章。笔者在2016年也发表过一篇关于CNN在文本分类方面的论文,今天写这篇博客的目的,是希望能对CNN的结构做一个比较清晰的阐述,同时就目前的研究现状做一个简单的总结,并对未来的发展方向做一个小小的期望。由于笔者在深度学习方面的资历尚浅,因此如文中出现错误,请不吝赐教。
一. CNN的结构阐述(以LeNet-5为例)
我写这一节的目的,并不是从头到尾的对CNN做一个详细的描述,如果你对CNN的结构不清楚,我建议还是先去看LeCun大神的论文Gradient-based learning applied to document recognition,而且,网上也有很多经典的博客,对CNN的结构和原理都做了比较深入的阐述,这里推荐zouxy大神的博客。这里对结构进行重新阐述,主要是对一些入门的同学可能会碰到的问题进行一些突出和讨论,并且主要围绕以下几个问题展开(一看就懂得大神请绕道):
我们先来看LeNet-5的结构图(LeNet共有3个C层2个S层,故被称为LeNet-5,如果算上F6和输出层,则可以被称为LeNet-7):
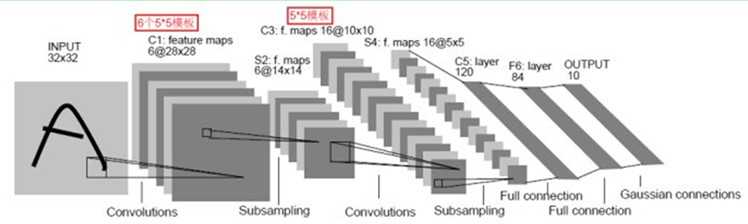
首先,我们先对CNN中的一些概念做一遍梳理。尤其需要注意的是Filter Window(卷积核的size,数字图像处理中一般为正方形),Feature Map(特征图,一般来说,对于每一个Filter Window有几个Feature Map,以捕捉不同的特征)。从图中我们可以看出,C1层的Feature Map是6,C3层的Feature Map是16,C5层的Feature Map是120,最后的F6相当于普通神经网络的隐层,通过全连接和C5相连,最后通过Gaussian Connection将其转换为一个10分类的问题。
针对第1个问题,卷积究竟是什么。卷积这个玩意儿在数字信号处理中经常被提及,它的数学表达式如下:
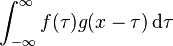
看到公式一般都比较头疼,所以在这里贴出来一个关于数字信号处理中的卷积的形象比喻:
比如说你的老板命令你干活,你却到楼下打台球去了,后来被老板发现,他非常气愤,扇了你一巴掌(注意,这就是输入信号,脉冲),于是你的脸上会渐渐地(贱贱地)鼓起来一个包,你的脸就是一个系统,而鼓起来的包就是你的脸对巴掌的响应,好,这样就和信号系统建立起来意义对应的联系。下面还需要一些假设来保证论证的严谨:假定你的脸是线性时不变系统,也就是说,无论什么时候老板打你一巴掌,打在你脸的同一位置(这似乎要求你的脸足够光滑,如果你说你长了很多青春痘,甚至整个脸皮处处连续处处不可导,那难度太大了,我就无话可说了哈哈),你的脸上总是会在相同的时间间隔内鼓起来一个相同高度的包来,并且假定以鼓起来的包的大小作为系统输出。好了,那么,下面可以进入核心内容——卷积了!
如果你每天都到地下去打台球,那么老板每天都要扇你一巴掌,不过当老板打你一巴掌后,你5分钟就消肿了,所以时间长了,你甚至就适应这种生活了……如果有一天,老板忍无可忍,以0.5秒的间隔开始不间断的扇你的过程,这样问题就来了,第一次扇你鼓起来的包还没消肿,第二个巴掌就来了,你脸上的包就可能鼓起来两倍高,老板不断扇你,脉冲不断作用在你脸上,效果不断叠加了,这样这些效果就可以求和了,结果就是你脸上的包的高度随时间变化的一个函数了(注意理解);如果老板再狠一点,频率越来越高,以至于你都辨别不清时间间隔了,那么,求和就变成积分了。可以这样理解,在这个过程中的某一固定的时刻,你的脸上的包的鼓起程度和什么有关呢?和之前每次打你都有关!但是各次的贡献是不一样的,越早打的巴掌,贡献越小,所以这就是说,某一时刻的输出是之前很多次输入乘以各自的衰减系数之后的叠加而形成某一点的输出,然后再把不同时刻的输出点放在一起,形成一个函数,这就是卷积,卷积之后的函数就是你脸上的包的大小随时间变化的函数。本来你的包几分钟就可以消肿,可是如果连续打,几个小时也消不了肿了,这难道不是一种平滑过程么?反映到剑桥大学的公式上,f(a)就是第a个巴掌,g(x-a)就是第a个巴掌在x时刻的作用程度,乘起来再叠加就ok了,大家说是不是这个道理呢?我想这个例子已经非常形象了,你对卷积有了更加具体深刻的了解了吗?(转自GSDzone论坛)
其实,在数字信号处理中,卷积就是信号B与信号A错开时间的内积,错开的时间长度就是卷积结果的自变量。但是,CNN中,卷积操作的作用是突出特征,将更明显的特征提取出来。那么这两个卷积是一样的吗?其实,在CNN中(尤其在自然语言处理的过程中),卷积的操作也是用一个公式来表示的:
$_i = f(\sum \omega \cdot x + bias)$
标签:
原文地址:http://www.cnblogs.com/yelbosh/p/5808706.html