标签:
本文属作者原创,转载请注明出处
http://www.cnblogs.com/qxred/p/dcalgorithm.html
本系列目录:
lanczos算法及C++实现(二)实对称阵奇异值分解的QR算法
lanczos算法及C++实现(三)实对称三对角阵特征值分解的分治算法
https://en.wikipedia.org/wiki/Divide-and-conquer_eigenvalue_algorithm
A. Melman Numerical solution of a secular equation
J Rutter A Serial Implementation of Cuppen‘s Divide and Conquer Algorithm for the Symmetric Eigenvalue Problem Chapter 3。本文的一些插图来自这篇文章。
在第一篇中,我们讨论了lanczos算法的基本框架。当我们用lanczos算法将一个实对称阵转化成三对角阵之后,我们可以用第二篇中的QR算法计算三对角阵的特征值特征向量。
本篇我们将讨论计算该三对角阵更加快速的算法——分治法(Divide and Conquer),该算法最早由Cuppen于1981年提出。
给定实对称三对角阵
分治法的基本思想是将T分成两块三对角阵,求得这两块三对角阵的特征值特征向量之后,再合并,求合并之后的特征值特征向量:
分(Divide):
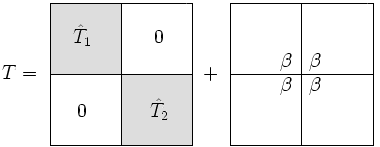
求的特征值分解:
合并(Conquer)
T可以表示为:
其中,





现在要求T的特征值分解,,可以先求
的特征值分解
,再令
如何求 的特征值分解呢?如果
则显然P=I。下面假设
假设是特征值,
是对应的特征向量,根据特征值定义我们有
假如D所有对角线元素各不相同,并且z的所有元素不为0 (这两个假设来自wiki,但是感觉没什么道理,anyway先pass)。可以证明。
反证法,否则,p是D的特征向量。因为D对角线元素各不相同,因此p只能有一个非0分量,而由于z所有分量非0,所以得到
由此我们有
或者写成如下形式:
其中
因此求特征值问题最后归结为求解一个方程的根。这个方程被称为"Secular Equation"。 该方程的解法下面会详细讨论,这里略过。得到特征值之后,根据 上面第二行 ,可以得出
是特征值
对应的特征向量。
至此我们得到了分治法的框架,总结如下:
[Q,D] = DivideAndConquer(T) //输入T实对称三对角阵,输出T的特征值分解T=Q D Q‘,Q为正交阵,每列为T的特征向量,D为对角阵,对角线元素为T的特征值 if T is 1x1 matrix Q=1, D=T else Divide

[Q1,D1]=DivideAndConquer() [Q2,D2]=DivideAndConquer(
)
let,
是
的最后一行,
是
的第一行。 Find eigen values
of
by solving Secular Equation
Get eigen vectors
of
using
Update eigen vectors of T:
return D=diag(
), Q end
这节讨论secular方程的解法,这里假设所有z非0,所有d各不相同。
任选一个i,作变量代换:
这样secular方程就变为
这个方程有n个根,且根各不相同,按照从小到大的顺序,记这n个根为。
不失一般性,假设,则有
, 对于j=n的情况,
举个例子,函数的图像如下
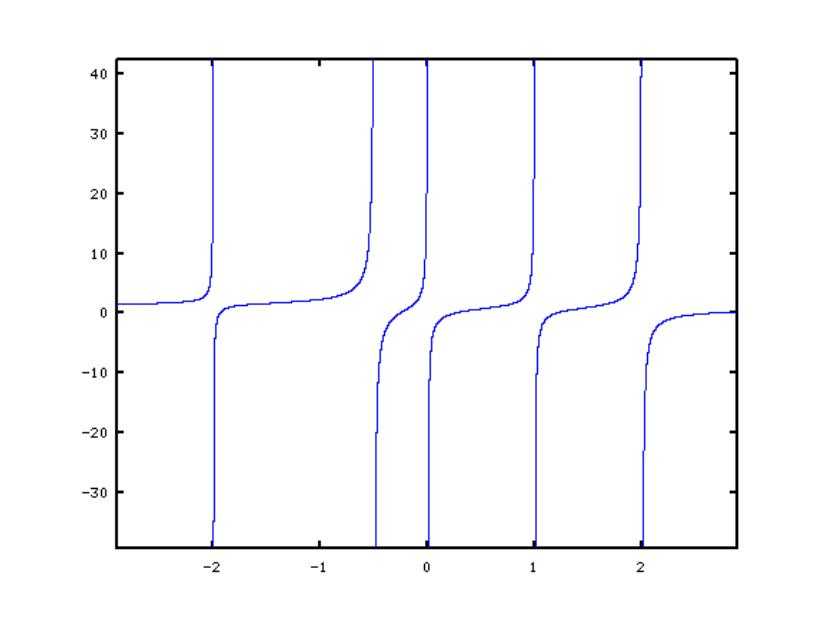
可以看到, 我们可以在区间
内求解第i个根。我们把这个区间放大,得到如下图像。
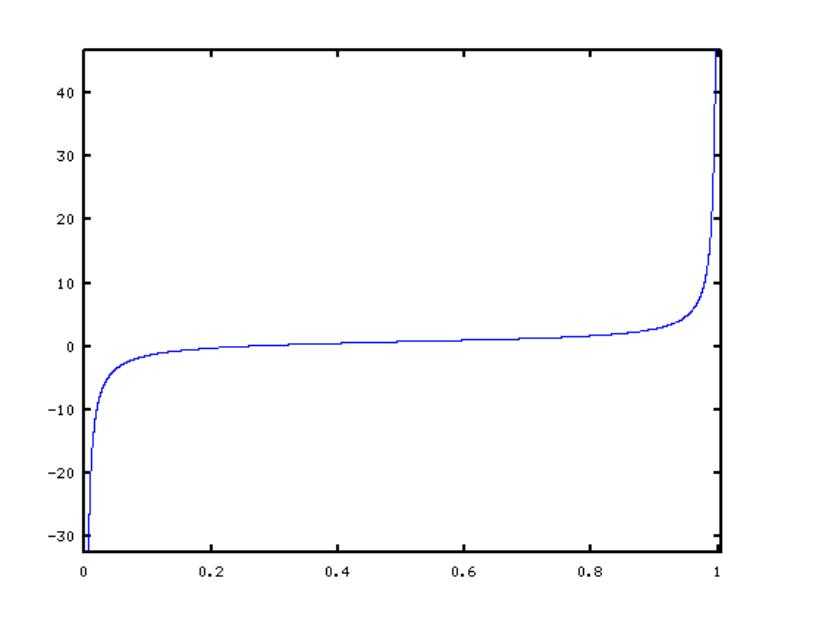
可以看到这段区间内,函数h单调增,与x轴有1个交点。如何求这个点呢,最简单的是2分法,可以在log时间内收敛。
更快的是牛顿迭代法。但是这里注意一个问题,就是如果初始点选的不好,牛顿法会发散,找不到根。如何保证牛顿法收敛呢?这里我们需要对变量作一个替换,
令
这样,原来的定义域就变成了
,对于i=n的情况,
现在我们看一下新的函数在区间
上的图像.
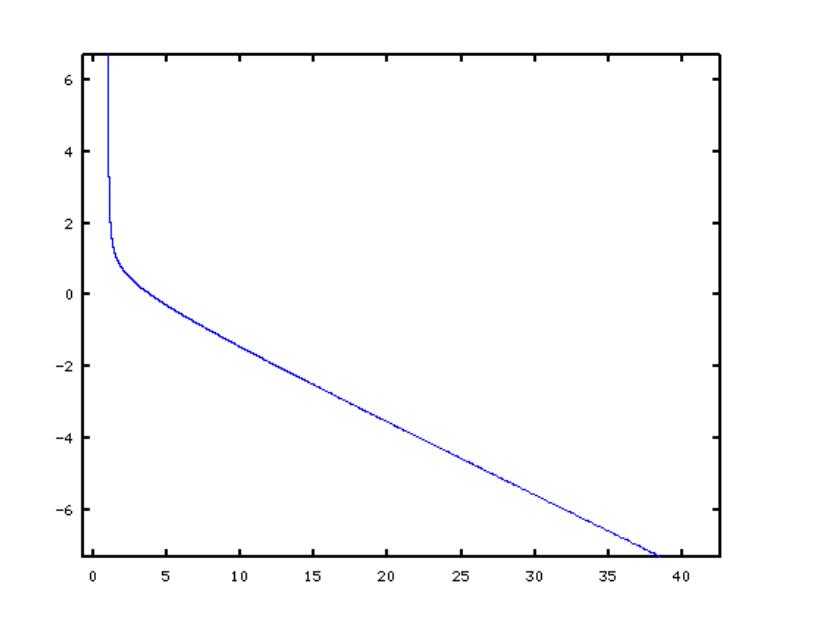
可见,在区间上,函数
单调递减。假设
的根为
,论文Numerical solution of a secular equation证明了,如果初始点选在
的左侧,则牛顿法必定收敛。换句话说,如果初始点
满足
,则用牛顿法得到的
序列收敛到
如何找这个初始点呢?论文Numerical solution of a secular equation构造了的一个下界函数
,通过求解
得到根
,则有
,从而求得初始点。
现在我们推出这个下界函数。先讨论i<n的情况,然后讨论i=n的情况。
我们直接通过函数来推出下界函数。根据前面所述,
当j<i时,,因此
当j>i时,,同样有
所以
这时,用带入,得到
令右边等于0,我们得到一个方程,通过通分,去分母,最后转成一个二次方程:
用求根公式可以得到两个解,注意定义域,因此取大根即可。
当i=n时,此时的定义域为,其实
也是有定义的,而且此时
是该函数的最左边的点,因此直接选取
作为初始点即可。
之后牛顿迭代:
一般两到三次迭代即可收敛,可以认为是O(1) 时间。
这里只讨论了分治算法最基本的实现,论文A Serial Implementation of Cuppen‘s Divide and Conquer Algorithm for the Symmetric Eigenvalue Problem还提到了用deflation加速,此外分治算法还有稳定性等问题。这里就不详细探讨了。
最后给出我的分治算法的实现,在函数void svds(SparseMatrix &A, int r, vector<vector<double> > &U, vector<double> &s, vector<vector<double> > &V, string algo)中,如果最后一个参数是“DC”怎表示用分治法解三对角阵的分解,如果algo="QR"则用前面一篇所述的QR算法求解三对角阵的分解。详见附录A。共有四个文件,fun.h提供一些常用的函数,比如归并排序等等,svds.cpp提供分治法的实现,也包括了前面的lanczos算法和QR算法的实现。svds.h是一个头文件。main.cpp提供main函数,一个调用奇异值分解的样例。编译用命令g++ main.cpp svds.cpp
main.cpp
#include "svds.h" #include <iostream> #include <cstdlib> int main(){ cout.precision(6); cout.setf(ios::fixed); srand(time(NULL)); SparseMatrix A; A.rows=10; A.cols=8; int rank=4; for(int i=0;i<A.rows;i++){ for(int j=0;j<A.cols;j++){ A.cells.push_back(Cell(i,j,rand()*1.0/RAND_MAX-0.5)); } } vector<vector<double> > U,V; vector<double> s; svds(A,rank,U,s,V); cout<<"[U,S,V]=svds(A,r)"<<endl; cout<<"r = "<<rank<<endl; cout<<"A = "<<endl; A.moveFirst(); for(int i=0;i<A.rows;i++){ for(int j=0;j<A.cols;j++) cout<<A.next().value<<‘ ‘; cout<<endl; } cout<<endl<<endl; cout<<endl<<endl; cout<<"U = "<<endl; print(U); cout<<"s = "<<endl; for(int i=0;i<s.size();i++){ for(int j=0;j<s.size();j++){ if(i==j) cout<<s[i]<<‘ ‘; else cout<<0.0<<‘ ‘; } cout<<endl; } cout<<endl; cout<<endl; cout<<"V = "<<endl; print(V); return 0; }
svds.h
#ifndef SVDS_H #define SVDS_H #include <vector> #include <string> using namespace std; class Cell{ public: unsigned int row; unsigned int col; double value; Cell():row(0),col(0),value(0){}; Cell(int r, int c, double v):row(r),col(c),value(v){}; }; class SparseMatrix{ public: unsigned int rows; unsigned int cols; vector<Cell> cells; int cellID; //read data sequentially, especially when loading large matrix from the disk. void moveFirst(){ cellID=0; } bool hasNext(){ return cellID<cells.size(); } Cell next(){ return cells[cellID++]; } }; void svds(SparseMatrix &A, int r, vector<vector<double> > &U, vector<double> &s, vector<vector<double> > &V, string algo="DC"); //decompose A = U * diag(s) *V‘ //where A is a m*n matrix //U is a m*r column orthogonal matrix //s is a length r vector //V is a n*r column orthogonal matrix void print(vector<vector<double> > &X); void hessenbergReduction(vector<vector<double> > &A, vector<vector<double> > &U); void QRHessenbergBasic(vector<vector<double> > &A, vector<vector<double> > &Q); void QRbasic(vector<vector<double> > &T, vector<vector<double> > &W); void transpose(vector<vector<double> > &A, vector<vector<double> > &T); void multiply(vector<vector<double> > &A, vector<vector<double> > &B, vector<vector<double> > &C); void QRHessenberg(vector<vector<double> > &A, vector<vector<double> > &Q); void QRTridiagonal(vector<vector<double> > &A, vector<vector<double> > &Q); #endif
svds.cpp
#include <iostream> #include <fstream> #include <vector> #include <string> #include <cmath> #include <climits> #include <cstdlib> #include <algorithm> #include <iomanip> #include "fun.h" #include "svds.h" using namespace std; const double EPS=1e-15; void print(vector<vector<double> > &X){ cout.precision(6); cout.setf(ios::fixed); for(int i=0;i<X.size();i++){ for(int j=0;j<X[i].size();j++) cout<<X[i][j]<<‘ ‘; cout<<endl; } cout<<endl; } void transpose(vector<vector<double> > &A, vector<vector<double> > &T){ if(A.empty()||A[0].empty()) return; int m=A.size(); int n=A[0].size(); T.clear(); T.resize(n,vector<double>(m,0)); for(int i=0;i<m;i++) for(int j=0;j<n;j++) T[j][i]=A[i][j]; } void transpose(vector<vector<double> > &A){ int m=A.size(); for(int i=0;i<m;i++) for(int j=i+1;j<m;j++) swap(A[i][j],A[j][i]); } void randUnitVector(int n, vector<double> &v){ srand(time(NULL)); v.clear();v.resize(n); while(true){ double r=0; for(int i=0;i<n;i++){ v[i]=rand()*1.0/RAND_MAX-0.5; r+=v[i]*v[i]; } r=sqrt(r); if(r>EPS){ for(int i=0;i<n;i++) v[i]/=r; break; } } } void multiply(vector<vector<double> > &A, vector<vector<double> > &B, vector<vector<double> > &C){ //C=A*B C.clear(); if(A.empty() || A[0].empty() || B.empty() || B[0].empty()) return ; C.resize(A.size(),vector<double>(B[0].size(),0)); for(int i=0;i<A.size();i++){ for(int j=0;j<B[0].size();j++){ C[i][j]=0; for(int k=0;k<A[0].size();k++){ C[i][j]+=A[i][k]*B[k][j]; } } } } void multiply(const vector<vector<double> > &X, const vector<double> & v, vector<double> & res){ res.clear(); if(X.empty() || v.empty()) return; int m=X[0].size(); res.resize(m,0); for(int i=0;i<m;i++){ for(int j=0;X[i].size();j++){ res[i]+=X[i][j]*v[j]; } } } double dotProduct(const vector<double> & a, const vector<double> & b){ double res=0; for(int i=0;i<a.size();i++) res+=a[i]*b[i]; return res; } void rightMultiply(SparseMatrix &A, const vector<double> & v, vector<double> & res){ //res= A*A‘*v int m=A.rows; int n=A.cols; res.clear(); res.resize(m,0); vector<double> w(n,0); A.moveFirst(); while(A.hasNext()){ Cell c=A.next(); w[c.col]+=c.value*v[c.row]; } A.moveFirst(); while(A.hasNext()){ Cell c=A.next(); res[c.row]+=c.value*w[c.col]; } } void leftMultiply(SparseMatrix &A, const vector<double> & v, vector<double> & res){ //res= A‘*A*v int m=A.rows; int n=A.cols; res.clear(); res.resize(n,0); vector<double> w(m,0); A.moveFirst(); while(A.hasNext()){ Cell c=A.next(); w[c.row]+=c.value*v[c.col]; } A.moveFirst(); while(A.hasNext()){ Cell c=A.next(); res[c.col]+=c.value*w[c.row]; } } void rightMultiply(const vector<vector<double> > & B,SparseMatrix &A, vector<vector<double> > & C){ //C= B‘*A int m=B[0].size(); int k=B.size(); int n=A.cols; for(int i=0;i<C.size();i++) fill(C[i].begin(),C[i].end(),0); A.moveFirst(); while(A.hasNext()){ Cell c=A.next(); for(int i=0;i<m;i++){ C[c.col][i]+=c.value*B[c.row][i]; } } } void leftMultiply(const vector<vector<double> > & B,SparseMatrix &A, vector<vector<double> > & C){ //C <- A B int r=B[0].size(); int n=B.size(); int m=A.rows; C.clear(); C.resize(m,vector<double>(r,0)); A.moveFirst(); while(A.hasNext()){ Cell c=A.next(); for(int i=0;i<r;i++){ C[c.row][i]+=c.value*B[c.col][i]; } } } double norm(const vector<double> &v){ double r=0; for(int i=0;i<v.size();i++) r+=v[i]*v[i]; return sqrt(r); } double normalize(vector<double> &v){ double r=0; for(int i=0;i<v.size();i++) r+=v[i]*v[i]; r=sqrt(r); if(r>EPS){ for(int i=0;i<v.size();i++) v[i]/=r; } return r; } void multiply(vector<double> &v, double d){ for(int i=0;i<v.size();i++) v[i]*=d; } void hessenbergReduction(vector<vector<double> > &A, vector<vector<double> > &U){ //A: m*m matrix //Reduction A to Hessenberg form: H=U‘AU (A=UHU‘), H overwrite A to save memory int m=A.size(); vector<double> v(m); U.clear(); U.resize(m,vector<double>(m,0)); for(int i=0;i<m;i++) U[i][i]=1; for(int i=1;i<m;i++){ fill(v.begin(),v.end(),0); for(int j=i;j<m;j++) v[j]=A[j][i-1]; v[i]-=norm(v); normalize(v); //P=I-2*v*v‘ //A=PAP //1. PA for(int j=i-1;j<m;j++){ double d=0; for(int k=i;k<m;k++) d+=A[k][j]*v[k]; for(int k=i;k<m;k++) A[k][j]-=d*2*v[k]; } //2. AP for(int j=0;j<m;j++){//row j double d=0; for(int k=i;k<m;k++) d+=A[j][k]*v[k]; for(int k=i;k<m;k++) A[j][k]-=d*2*v[k]; } //U=U*P for(int j=0;j<m;j++){ double d=0; for(int k=i;k<m;k++) d+=U[j][k]*v[k]; for(int k=i;k<m;k++) U[j][k]-=d*2*v[k]; } } } void givensRotation(double a, double b, double &c, double &s){ if(fabs(b)<EPS){ c=1;s=0; }else{ if(fabs(b)>fabs(a)){ double r=a/b; s=1/sqrt(1+r*r); c=s*r; }else{ double r=b/a; c=1/sqrt(1+r*r); s=c*r; } } } void QRTridiagonal(vector<vector<double> > &A, vector<vector<double> > &Q){ //input: A m*m symmetry tridiagonal matrix //output: Upper triangular R, and orthogonal Q, such that A=QRQ‘ int n=A.size(); Q.clear(); Q.resize(n,vector<double>(n,0)); vector<double> cs(n-1,0); vector<double> ss(n-1,0); for(int i=0;i<n;i++) Q[i][i]=1; for(int m=n;m>=2;m--){ while(1){ fill(cs.begin(),cs.end(),0); fill(ss.begin(),ss.end(),0); double delta=(A[m-2][m-2]-A[m-1][m-1])/2; double sign=1; if(delta<0) sign=-1; //Wilkinson shift double shift=A[m-1][m-1]-sign*A[m-1][m-2]*A[m-2][m-1]/(fabs(delta)+sqrt(delta*delta+A[m-1][m-2]*A[m-2][m-1])); for(int i=0;i<m;i++) A[i][i]-=shift; for(int i=0;i<m-1;i++){ double a=A[i][i]; double b=A[i+1][i]; givensRotation(a,b,cs[i],ss[i]); for(int j=i;j<=i+2 && j<m;j++){ a=A[i][j]; b=A[i+1][j]; A[i][j]=cs[i]*a+ss[i]*b; A[i+1][j]=-ss[i]*a+cs[i]*b; } } for(int j=1;j<m;j++){// cols j-1, j c -s for(int i=max(0,j-2);i<=j;i++){// rows 0 ... j [a ,b] s c double a=A[i][j-1]; double b=A[i][j]; A[i][j-1]=cs[j-1]*a+ss[j-1]*b; A[i][j]=-ss[j-1]*a+cs[j-1]*b; } } for(int i=0;i<m;i++) A[i][i]+=shift; //Q=Q*G1...Gm for(int j=1;j<m;j++){ for(int i=0;i<n;i++){ double a=Q[i][j-1]; double b=Q[i][j]; Q[i][j-1]=cs[j-1]*a+ss[j-1]*b; Q[i][j]=-ss[j-1]*a+cs[j-1]*b; } } if(fabs(A[m-1][m-2])<1e-10) break; } } } vector<double> secularEquationSolver(vector<double> &z, vector<double> &D, double sigma){ //solve equation // 1 + \sigma \sum_j \frac{b^2_j}{d_j-\lambda} =0 int n=z.size(); vector<double> res(n); //sort : d_0 < d_1 < ... < d_{n-1} vector<int> index; vector<double> d(n); merge_sort(D,index); if(sigma<0) reverse(index.begin(),index.end()); vector<double> b(n); for(int i=0;i<n;i++){ b[i]=z[index[i]]; d[i]=D[index[i]]; } vector<double> lambda(n); for(int i=0;i<n;i++){ vector<double> delta(d.size()); for(int j=0;j<delta.size();j++) delta[j]=(d[j]-d[i])/sigma; double gamma=0; if(i+1<n){ //gamma>1/delta[i+1] double A=b[i]*b[i]; double B=-A/delta[i+1]-1; for(int j=0;j<delta.size();j++) if(j!=i) B-=b[j]*b[j]/delta[j]; double C=1; for(int j=0;j<delta.size();j++) if(j!=i) C+=b[j]*b[j]/delta[j]; C/=delta[i+1]; C-=b[i+1]*b[i+1]/delta[i+1]; gamma=(-B+sqrt(B*B-4*A*C))/(2*A); } //start Newton double diff=1; while(diff*diff>EPS){ double g=0; for(int j=0;j<n;j++){ g-=b[j]*b[j]/((delta[j]*gamma-1)*(delta[j]*gamma-1)); } double f=1; for(int j=0;j<n;j++){ f+=b[j]*b[j]/(delta[j]-1/gamma); } //f+g(newGamma-gamma)=0 double newGamma=-f/g+gamma; diff=fabs(newGamma-gamma); gamma=newGamma; } lambda[i]=1/gamma*sigma+d[i]; } for(int i=0;i<n;i++) res[index[i]]=lambda[i]; return res; } void DCSub(vector<double> &alpha, vector<double> &beta, vector<vector<double> > &Q, vector<double> &D, int start, int end){ if(start==end){ Q[start][start]=1; D[start]=alpha[start]; return; }else{ int mid=(start+end)/2; // | mid mid+1 //--------------------------------------------- // mid | a(mid) b(mid+1) // mid+1 | b(mid+1) a(mid+1) alpha[mid]-=beta[mid+1]; alpha[mid+1]-=beta[mid+1]; DCSub(alpha,beta,Q,D,start,mid); DCSub(alpha,beta,Q,D,mid+1,end); //alpha[mid]+=beta[mid+1]; //alpha[mid+1]+=beta[mid+1]; int n=end-start+1; vector<double> z(n,0); for(int i=start;i<=mid;i++) z[i-start]=Q[mid][i]; for(int i=mid+1;i<=end;i++) z[i-start]=Q[mid+1][i]; //calculate eigen systems of matrix D+beta[mid+1]*z*z‘ vector<double> d(n,0); for(int i=0;i<n;i++) d[i]=D[i+start]; //secular equation is: // 1 + \sum_j \frac{z^2_j}{d_j-\lambda} =0 vector<double> lambda=secularEquationSolver(z, d, beta[mid+1]); //eigen vector: //P = (D-\lambda I)^{-1} z vector<vector<double> > P(n,vector<double>(n)); for(int i=0;i<n;i++){//for each eigen value vector<double> p(n); for(int j=0;j<n;j++) p[j]=1.0/(D[j+start]-lambda[i])*z[j]; normalize(p); for(int j=0;j<n;j++) P[j][i]=p[j]; } vector<vector<double> > oldQ(n,vector<double>(n)); for(int i=0;i<n;i++) for(int j=0;j<n;j++){ oldQ[i][j]=Q[i+start][j+start]; } for(int i=0;i<n;i++){ for(int j=0;j<n;j++){ Q[i+start][j+start]=0; for(int k=0;k<n;k++){ Q[i+start][j+start]+=oldQ[i][k]*P[k][j]; } } } //eigen value for(int i=0;i<n;i++) D[i+start]=lambda[i]; } } void DCTridiagonal(vector<double> alpha, vector<double> &beta, vector<vector<double> > &Q, vector<double> &D){ //input: A m*m symmetry tridiagonal matrix //output: diagonal matrix D, and orthogonal D, such that A=QRQ‘ int m=alpha.size(); Q.clear(); Q.resize(m,vector<double>(m,0)); D.clear(); D.resize(m,0); DCSub(alpha, beta, Q, D, 0, m-1); } void QRHessenberg(vector<vector<double> > &A, vector<vector<double> > &Q){ //input: A m*m square Hessenberg Matrix //output: Upper triangular R, and orthogonal Q, such that A=QRQ‘ int n=A.size(); Q.clear(); Q.resize(n,vector<double>(n,0)); vector<double> cs(n-1,0); vector<double> ss(n-1,0); for(int i=0;i<n;i++) Q[i][i]=1; for(int m=n;m>=2;m--){ while(1){ fill(cs.begin(),cs.end(),0); fill(ss.begin(),ss.end(),0); double delta=(A[m-2][m-2]-A[m-1][m-1])/2; double sign=1; if(delta<0) sign=-1; //Wilkinson shift double shift=A[m-1][m-1]-sign*A[m-1][m-2]*A[m-2][m-1]/(fabs(delta)+sqrt(delta*delta+A[m-1][m-2]*A[m-2][m-1])); for(int i=0;i<m;i++) A[i][i]-=shift; for(int i=0;i<m-1;i++){ double a=A[i][i]; double b=A[i+1][i]; givensRotation(a,b,cs[i],ss[i]); for(int j=i;j<m;j++){ a=A[i][j]; b=A[i+1][j]; A[i][j]=cs[i]*a+ss[i]*b; A[i+1][j]=-ss[i]*a+cs[i]*b; } } for(int j=1;j<m;j++){// cols j-1, j c -s for(int i=0;i<=j;i++){// rows 0 ... j [a ,b] s c double a=A[i][j-1]; double b=A[i][j]; A[i][j-1]=cs[j-1]*a+ss[j-1]*b; A[i][j]=-ss[j-1]*a+cs[j-1]*b; } } for(int i=0;i<m;i++) A[i][i]+=shift; //Q=Q*G1...Gm for(int j=1;j<m;j++){ for(int i=0;i<n;i++){ double a=Q[i][j-1]; double b=Q[i][j]; Q[i][j-1]=cs[j-1]*a+ss[j-1]*b; Q[i][j]=-ss[j-1]*a+cs[j-1]*b; } } if(fabs(A[m-1][m-2])<1e-10) break; } } } void QRHessenbergBasic(vector<vector<double> > &A, vector<vector<double> > &Q){ //input: A m*m square Hessenberg Matrix //output: Upper triangular R such taht A=QRQ‘ for orthogonal matrix Q int m=A.size(); vector<double> cs(m-1,0); vector<double> ss(m-1,0); double diff=1; Q.clear(); Q.resize(m,vector<double>(m,0)); for(int i=0;i<m;i++) Q[i][i]=1; while(1){ for(int i=0;i<m-1;i++){ double a=A[i][i]; double b=A[i+1][i]; givensRotation(a,b,cs[i],ss[i]); for(int j=i;j<m;j++){ a=A[i][j]; b=A[i+1][j]; A[i][j]=cs[i]*a+ss[i]*b; A[i+1][j]=-ss[i]*a+cs[i]*b; } } for(int j=1;j<m;j++){// cols j-1, j c -s for(int i=0;i<=j;i++){// rows 0 ... j [a ,b] s c double a=A[i][j-1]; double b=A[i][j]; A[i][j-1]=cs[j-1]*a+ss[j-1]*b; A[i][j]=-ss[j-1]*a+cs[j-1]*b; } } //Q=Q*G1...Gm for(int j=1;j<m;j++){ for(int i=0;i<m;i++){ double a=Q[i][j-1]; double b=Q[i][j]; Q[i][j-1]=cs[j-1]*a+ss[j-1]*b; Q[i][j]=-ss[j-1]*a+cs[j-1]*b; } } diff=0; for(int i=0;i+1<m;i++){ diff+=A[i+1][i]*A[i+1][i]; } diff=sqrt(diff); if(diff<1e-10) break; } } void QRFactorization(vector<vector<double> > &A, vector<vector<double> > &Q, vector<vector<double> > &R){ //A=Q*R //A: m*n matrix //Q: m*m matrix //R: m*n matrix int m=A.size(); int n=A[0].size(); for(int i=0;i<Q.size();i++) fill(Q[i].begin(),Q[i].end(),0); for(int i=0;i<R.size();i++) fill(R[i].begin(),R[i].end(),0); vector<double> q(m); vector<double> r(n); for(int i=0;i<n;i++){ for(int j=0;j<m;j++) q[j]=A[j][i]; fill(r.begin(),r.end(),0); for(int j=0;j<i && j<m;j++){ r[j]=0; for(int k=0;k<q.size();k++) r[j]+=Q[k][j]*q[k]; for(int k=0;k<q.size();k++) q[k]-=Q[k][j]*r[j]; } if(i<m){ r[i]=normalize(q); for(int j=0;j<m;j++) Q[j][i]=q[j]; } for(int j=0;j<m;j++){ R[j][i]=r[j]; } } } void lanczos(SparseMatrix &A, vector<vector<double> > &P, vector<double> &alpha, vector<double> &beta, unsigned int rank){ //P‘*A*A‘*P = T = diag(alpha) + diag(beta,1) + diag(beta, -1) //P=[p1,p2, ... , pk] rank=min(A.cols,min(A.rows,rank)); vector<double> p; unsigned int m=A.rows; unsigned int n=A.cols; vector<double> prevP(m,0); randUnitVector(m,p); P.clear(); P.resize(m,vector<double>(rank,0)); vector<double> v; alpha.clear();alpha.resize(rank); beta.clear();beta.resize(rank); beta[0]=0; for(int i=0;i<rank;i++){ for(int j=0;j<p.size();j++){ P[j][i]=p[j]; } rightMultiply(A, p, v); alpha[i]=dotProduct(p,v); if(i+1<rank){ for(int j=0;j<m;j++) v[j]=v[j]-beta[i]*prevP[j]-alpha[i]*p[j]; beta[i+1]=norm(v); prevP=p; for(int j=0;j<m;j++) p[j]=v[j]/beta[i+1]; } } } void lanczosT(SparseMatrix &A, vector<vector<double> > &P, vector<double> &alpha, vector<double> &beta, unsigned int rank){ //P‘*A‘*A*P = T = diag(alpha) + diag(beta,1) + diag(beta, -1) //P=[p1,p2, ... , pk] rank=min(A.cols,min(A.rows,rank)); vector<double> p; unsigned int m=A.rows; unsigned int n=A.cols; vector<double> prevP(n,0); randUnitVector(n,p); P.clear(); P.resize(n,vector<double>(rank,0)); vector<double> v; alpha.clear();alpha.resize(rank); beta.clear();beta.resize(rank); beta[0]=0; for(int i=0;i<rank;i++){ for(int j=0;j<p.size();j++){ P[j][i]=p[j]; } leftMultiply(A, p, v); alpha[i]=dotProduct(p,v); if(i+1<rank){ for(int j=0;j<n;j++) v[j]=v[j]-beta[i]*prevP[j]-alpha[i]*p[j]; beta[i+1]=norm(v); prevP=p; for(int j=0;j<n;j++) p[j]=v[j]/beta[i+1]; } } } void QRbasic(vector<vector<double> > &T, vector<vector<double> > &W){ int l=T.size(); W.clear(); W.resize(l,vector<double>(l,0)); vector<vector<double> > Q(l,vector<double>(l,0)); vector<vector<double> > R(l,vector<double>(l,0)); vector<vector<double> > nextW(l,vector<double>(l,0)); for(int i=0;i<l;i++) W[i][i]=1; while(true){ //T=Q*R QRFactorization(T,Q,R); //T=R*Q multiply(R,Q,T); //W=W*Q; multiply(W,Q,nextW); double diff=0; for(int i=0;i<l;i++) for(int j=0;j<l;j++) diff+=(W[i][j]-nextW[i][j]) * (W[i][j]-nextW[i][j]); W=nextW; if(diff<EPS*EPS) break; } } void svds(SparseMatrix &A, int r, vector<vector<double> > &U, vector<double> &s, vector<vector<double> > &V, string algo){ //A=U*diag(s)*V‘ //A:m*n matrix sparse matrix //U:m*r matrix, U[i]=i th left singular vector //s:r vector //V:n*r matrix, V[i]=i th right singular vector int m=A.rows; int n=A.cols; //lanczos: A*A‘=P*T*P‘ if(m<=n){ int l=m; vector<vector<double> > P(m,vector<double>(l,0)); vector<double> alpha(l,0); vector<double> beta(l,0); lanczos(A,P,alpha,beta,l); vector<vector<double> > W; if(algo=="QR"){ vector<vector<double> > T(l,vector<double>(l,0)); for(int i=0;i<l;i++){ T[i][i]=alpha[i]; if(i) T[i-1][i]=T[i][i-1]=beta[i]; } QRTridiagonal(T,W); }else if(algo=="DC"){ vector<double> D(l,0); vector<vector<double> > Q; DCTridiagonal(alpha,beta,Q,D); //need sort vector<int> index; merge_sort(D,index); reverse(index.begin(),index.end()); W.resize(l,vector<double>(l)); for(int i=0;i<l;i++) for(int j=0;j<l;j++) W[i][j]=Q[i][index[j]]; } U.clear();U.resize(m,vector<double>(l)); multiply(P,W,U); for(int i=0;i<U.size();i++) U[i].resize(r); V.clear();V.resize(n,vector<double>(r)); rightMultiply(U,A,V); s.clear();s.resize(r,0); for(int i=0;i<r;i++){ for(int j=0;j<n;j++) s[i]+=V[j][i]*V[j][i]; s[i]=sqrt(s[i]); if(s[i]>EPS){ for(int j=0;j<n;j++) V[j][i]/=s[i]; } } }else{ int l=n; vector<vector<double> > P(n,vector<double>(l,0)); vector<double> alpha(l,0); vector<double> beta(l,0); lanczosT(A,P,alpha,beta,l); vector<vector<double> > W; if(algo=="QR"){ vector<vector<double> > T(l,vector<double>(l,0)); for(int i=0;i<l;i++){ T[i][i]=alpha[i]; if(i) T[i-1][i]=T[i][i-1]=beta[i]; } QRTridiagonal(T,W); }else if(algo=="DC"){ vector<double> D(l,0); vector<vector<double> > Q; DCTridiagonal(alpha,beta,Q,D); //need sort vector<int> index; merge_sort(D,index); reverse(index.begin(),index.end()); W.resize(l,vector<double>(l)); for(int i=0;i<l;i++) for(int j=0;j<l;j++) W[i][j]=Q[i][index[j]]; } V.clear();V.resize(n,vector<double>(l,0)); U.clear();U.resize(m,vector<double>(r,0)); multiply(P,W,V); for(int i=0;i<V.size();i++) V[i].resize(r); leftMultiply(V,A,U); s.clear();s.resize(r,0); for(int i=0;i<r;i++){ for(int j=0;j<m;j++) s[i]+=U[j][i]*U[j][i]; s[i]=sqrt(s[i]); if(s[i]>EPS){ for(int j=0;j<m;j++) U[j][i]/=s[i]; } } } }
fun.h
#ifndef FUN_H #define FUN_H #include <vector> using namespace std; template <class T> void combine(vector<T> &v, int left, int m, int right, vector<int> &index) { vector<T> tempv(v.begin()+left,v.begin()+right+1); vector<int> tempindex(index.begin()+left,index.begin()+right+1); int left_size=m-left+1; int size=right-left+1; int middle=m-left+1; int i=0; int j=middle; int k=left; while(i<left_size && j<size) { if(tempv[i]<=tempv[j]) { v[k]=tempv[i]; index[k]=tempindex[i]; k++; i++; }else{ v[k]=tempv[j]; index[k]=tempindex[j]; k++; j++; } } while(i<left_size) { v[k]=tempv[i]; index[k]=tempindex[i]; k++; i++; } } template <class T> void merge_sort(vector<T> &v, int left, int right, vector<int> &index) { if (left<right) { int m=(left+right)/2; merge_sort(v,left, m,index); merge_sort(v,m+1, right, index); combine(v,left, m, right,index); } } template <class T> void merge_sort(vector<T> v, vector<int> &index) //index[i] is the original index of i th best element { index.clear(); index.resize(v.size()); for(int i=0;i<v.size();i++) index[i]=i; merge_sort(v,0,v.size()-1,index); } #endif
lanczos算法及C++实现(三)实对称三对角阵特征值分解的分治算法
标签:
原文地址:http://www.cnblogs.com/qxred/p/dcalgorithm.html