标签：
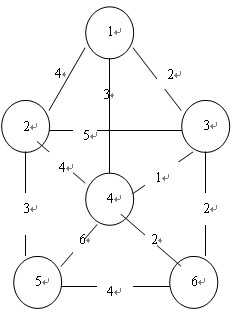所谓生成树，就是n个点之间连成n-1条边的图形。而最小生成树，就是权值（两点间直线的值）之和的最小值。
首先，要用二维数组记录点和权值。如上图所示无向图：
int map[7][7];
map[1][2]=map[2][1]=4;
map[1][3]=map[3][1]=2;
......
然后再求最小生成树。具体方法是：
1.先选取一个点作起始点，然后选择它邻近的权值最小的点（如果有多个与其相连的相同最小权值的点，随便选取一个）。如1作为起点。
visited[1]=1;
pos=1;
//用low[]数组不断刷新最小权值，low[i](0<i<=点数)的值为：i点到邻近点（未被标记）的最小距离。
low[1]=0; //起始点i到邻近点的最小距离为0
low[2]=map[pos][2]=4;
low[3]=map[pos][3]=2;
low[4]==map[pos][4]=3;
low[5]=map[pos][5]=MaxInt; //无法直达
low[6]=map[pos][6]=MaxInt;
2.再在伸延的点找与它邻近的两者权值最小的点。
//low[]以3作当前位置进行更新
visited[3]=1;
pos=3;
low[1]=0; //已标记，不更新
low[2]=map[1][2]=4; //比5小，不更新
low[3]=2; //已标记，不更新
low[4]=map[1][4]=3; //比1大，更新后为：low[4]=map[3][4]=1;
low[5]=map[1][5]=MaxInt;//无法直达，不更新
low[6]=map[1][6]=MaxInt;//比2大，更新后为：low[6]=map[3][6]=2;
3.如此类推...
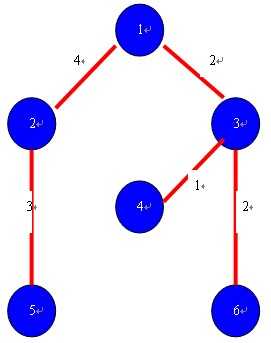
所有权值相加就是最小生成树，其值为2+1+2+4+3=12。
至于具体代码如何实现，现在结合POJ1258例题解释。代码如下：
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
|
#include <stdio.h>#include <string.h>#define MaxInt 0x3f3f3f3f#define N 110//创建map二维数组储存图表，low数组记录每2个点间最小权值，visited数组标记某点是否已访问int map[N][N],low[N],visited[N];int n;int prim(){ int i,j,pos,min,result=0; memset(visited,0,sizeof(visited));//从某点开始，分别标记和记录该点 visited[1]=1;pos=1;//第一次给low数组赋值 for(i=1;i<=n;i++) if(i!=pos) low[i]=map[pos][i];//再运行n-1次 for(i=1;i<n;i++) {//找出最小权值并记录位置 min=MaxInt; for(j=1;j<=n;j++) if(visited[j]==0&&min>low[j]) { min=low[j];pos=j; }//最小权值累加 result+=min;//标记该点 visited[pos]=1;//更新权值 for(j=1;j<=n;j++) if(visited[j]==0&&low[j]>map[pos][j]) low[j]=map[pos][j]; } return result;}int main(){ int i,v,j,ans; while(scanf("%d",&n)!=EOF) {//所有权值初始化为最大 memset(map,MaxInt,sizeof(map)); for(i=1;i<=n;i++) for(j=1;j<=n;j++) { scanf("%d",&v); map[i][j]=map[i][j]=v; } ans=prim(); printf("%d\n",ans); } return 0;} |
标签：
原文地址：http://www.cnblogs.com/weizhixiang/p/5816010.html
