标签:
题目:给两个字符串s和m,问m是否是s中的子串?
这是一个字符串匹配问题,我们可以直观的想到最简单的办法,就是两个循环,s从第一个到s.length - m.length。这个方法可以很好的解决问题,当然这里只是解决问题,并不能效率很高的解决。下面我们来看一下KMP算法是怎么样把时间复杂度降低到O(n)的,这里不分析时间复杂度,当然在算法实现的过程中你就可以发现这是O(n)的。
首先,我们来看一下定义:
最大前缀与最大后缀的匹配:当前字符前面的所有字符中,如果从头开始(前缀,但是不能包含最后一个字符,也就是当前字符的前一个)和从最后(后缀,从当前字符串的前一个开始,但是不包括第一个字符)得到的字符串一样(可以是任意长度的,并不一定完全匹配上,前缀和后缀可以重合也可以不重合),在所有的这样的字符创中,长度最长的一个就是最大前缀与最大后缀的匹配。举个例子:
字符创:abcabcd,对于d来说abc是最长的匹配。对于aaaab字符串中的b来说,最长匹配是aaa,长度为3。对于abd中的d来说,没有能够匹配的,长度为0.
我们有了上面的概念,下边看一下如果匹配的。
首先按照最大前缀和最大后缀匹配,对m进行计算,得到一个和m长度相等的数组,我们叫next数组,没错这就是大名鼎鼎的next数组,我们假设已经得到了这个数组,来看是如何利用next数组进行匹配。next数组的计算后面详述。
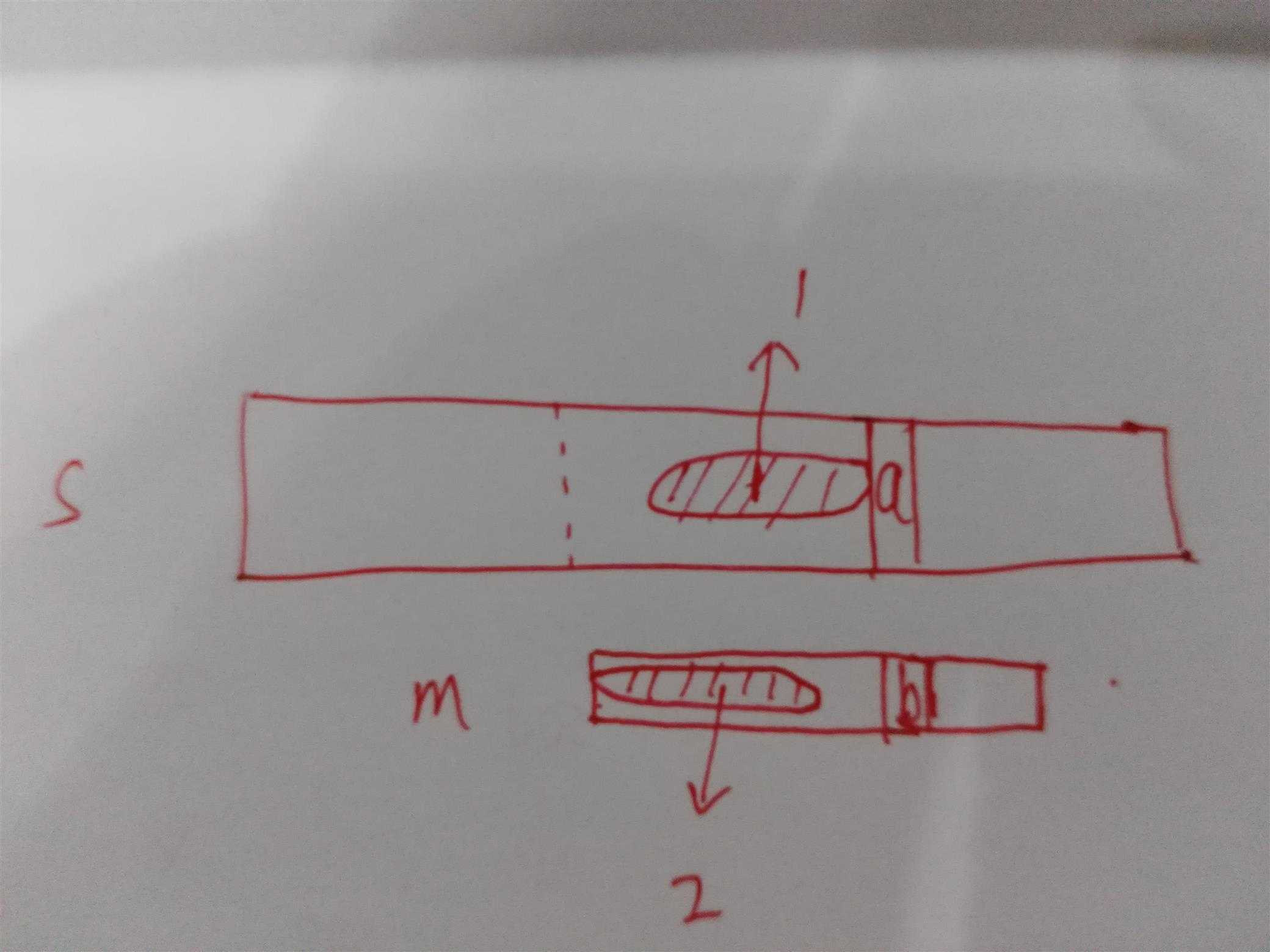
s为原字符串,m为匹配字符串。假设正在匹配s中a位置的字符,m中为b,这时候不相等。b之前的都是匹配好了的。1和2部分分别代表m的最大前缀和最大后缀,其实1应该画在m上,但是画在m上太乱了,只好画在s上,为什么能这样呢?因为现在已经匹配到了a、b位置,在s的a为之前和m的b位置前是相等的,因此画在s上表示也是可以的。(s中从虚线向后与m匹配的)
这时候a和b不相等,因此不能继续匹配下去。这时候要把m向右移动,移动多少呢?在一般的算法中,移动一个,但是这里KMP算法利用了之前比较的结果。那么移动到哪里呢,移动到1和2重合!至于1和2为什么相等的长度是多少,我们在next数组中可以得到,next数组代表的什么意义?代表最大前缀和最大后缀的长度。为了让1,2重合,s的比较位置不变,m的比较位置变成next[b位置下标],为最大前缀的长度,即2的长度。
对于在这个1和2重合的这里之前,虚线之后的都不用考虑,一定不存在匹配的情况。利用反证法证明,假设在虚线和1、2重合位置中间有一个位置使字符串匹配成功,那么这时候在这个位置到a位置是和m匹配的,因为m整个都匹配了,m的一部分也一定匹配上了。再回到现在这个图中,是不是1向前和2向后还是能接着匹配上,也就是说我们的最大前缀和最大后缀匹配长度比现在更长,next数组中的值是错的!所以在1、2重合之间一定不存在m匹配上s的情况,所以直接把m移动到1和2重合即可,这时候的比较是从1的开头位置比较的,由于之前比较过,在next数组中存在的数据可以利用,因此没有必要这一块重新比较,而是接着a这个位置和m的next[b位置下标]开始比较即可。
下面看一下比较的代码:
public static int kmpCom(String s, String m) { char[] str = s.toCharArray(); char[] match = m.toCharArray(); int si = 0; int mi = 0; int[] next = getNext(match);// 首先得到next数组,用上面的函数 while (si < str.length && mi < match.length) { if (str[si] == match[mi]) { /*如果相等则向后移动 * */ si++; mi++; } else if (next[mi] == -1) { /*如果第一个就不相等(next数组只有第一个为-1),那么原数组向后移动,比较下一个位置 * 这里第一个指的是m字符串的第一个,如果m的第一个跟s中的不匹配,那么就向后移动,后面还是m的第一个比 * */ si++; } else { /* 如果遇到不相等的,且m不是第一个位置,那么使用next数组,相当于m向右移动 * next数组表示m中当前位置最大前缀和最大后缀匹配的个数。 * 如前面有3个匹配,数组下表为3,表示从第4个开始比较 * */ mi = next[mi]; } } return mi == match.length ? si - mi : -1; }
上面讲述了字符串比较匹配的过程,下面看一下最重要的next数组的获得:
对于next求解,可以利用定义求解,不过这个办法复杂度太高了,我们要用一个复杂度较低的办法。看下面

假设我们i-1之前的都计算完成了,现在计算i位置的next数组值。图中的椭圆代表已经配上了。
1、第一幅图i-1位置为a,也就是像长方形下面这样两个匹配上了。这时候i和a后面的字符也一样匹配上了,那么next[i] = next[i-1] + 1.因为前面已经匹配上了,不需要重新计算,利用之前(i-1位置)的匹配结果就可以得到。
2、i位置和a后面的没有匹配上,如下面这个长方形的情况。那么就这要与这个字符串的next[a位置]位置比较,在途中也就是b位置,如果还没有匹配上在接着向前。为什么呢?我们a的最大前缀和后缀匹配是b两边的椭圆部分。因为i-1位置是匹配成功的,所以a之前的与i-1之前的都匹配上了,也就是b两边椭圆匹配,那么在i-1位置之前也应该有这样的两个区域,因为要的是最大前缀和后缀,那么i-1之前的两个椭圆后面的一定跟b左边的椭圆一样,那么接下来就要看一下i-1位置是不是与b位置相等。到哪里结束呢,当前是到不能向前移动的时候,也就是0位置。
这就是大概的过程,只用了文字叙述,因为画图比较费时间,但文字应该可以叙述清楚了。下面看一下代码:
1 public static int[] getNext(char[] ms) { 2 if (ms.length == 1) { 3 return new int[] { -1 }; 4 } 5 int[] next = new int[ms.length]; 6 next[0] = -1; 7 next[1] = 0; 8 int pos = 2;// 遍历到的位置 9 int cn = 0;// 10 while (pos < next.length) { 11 if (ms[pos - 1] == ms[cn]) { 12 next[pos++] = ++cn; 13 } else if (cn > 0) { 14 cn = next[cn]; 15 } else { 16 next[pos++] = 0; 17 } 18 } 19 return next; 20 }
这里需要注意的是初始化next[0] = -1, next[1] = 0.想一下next数组的定义,也能理解了。
标签:
原文地址:http://www.cnblogs.com/worsun/p/5831529.html