标签:
背包问题:
又是经历了一个非常痛苦的阶段,终于解决了一个非常简单而经典的动态规划问题。
问题描述:
一个旅行者随身带一个背包。可以放背包的物品有n种,每种物品的重量和价值分别为w和v。背包的最大重量限制是b,每种物品可以放多个,怎么放可以使背包价值最大?
思路:
1. 这一道问题属于线性规划问题:由线性约束的线性函数取最大或者最小问题。
2. 划分子问题:
有参数k和y界定:
k:考虑物品1,2,3.。。。。。。k的选择
y:背包的总重量不能超过y
原始输入, k = n, y = b
子问题计算顺序:
k = 1,2,3,.... n
对于给定的k,y = 1,2,3,.....b
3. 优化函数的递推方程:
Fk(y): 装前k种物品总重量不能超过y背包所能达到的最大价值
![]()
4. 初始状态的定义:
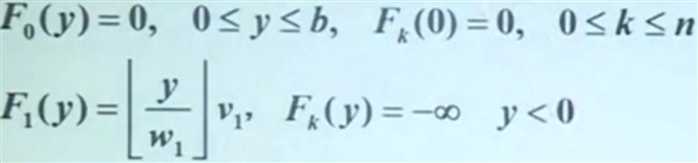
5. 标记函数:
这一问题不仅需要计算最大价值,而且还需要再标记出最大价值的物品编号,因此还需要另外一个函数来作为标记函数。
标记函数ik(y)

6.一个实例:
有四个物品,分别是下列输入,总重量不超过10
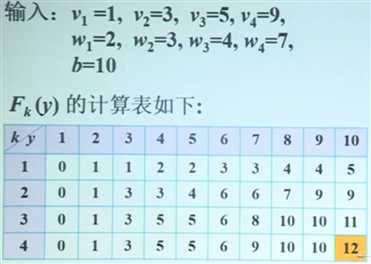
追踪解:
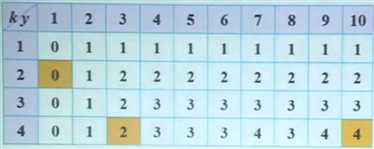
7. 解题心得:
1. 一定要注意边界上的元素,在动态规划中dp[0][i]与dp[j][0]是非常重要的,初始化的时候不能忽略,因为这一行和一列元素会作为后续问题解。
2. 对于备忘录数据结构中元素的意义与问题中给出的数据要合理对应上,还是需要考虑0的意义,虽然物品和重量编号可能从1开始,但是0的存在也是合理对应的一部分。
8.参考代码:
1 public static int[] BackDP(ArrayList<BagItem> items, int b){ 2 int[] result = new int[items.size()+1]; 3 int Num = items.size(); 4 int[][] dp = new int[Num][b+1]; 5 int[][] trace = new int[Num][b+1]; 6 for(int i = 0; i <=b; i++){ 7 dp[0][i] = ((i)/items.get(0).getWeight())*items.get(0).getValue(); 8 trace[0][i]=1; 9 } 10 11 trace[0][0] =0; 12 for(int i = 1; i<Num; i++){ 13 for(int j = 0; j<=b; j++){ 14 int TryWeight = j - items.get(i).getWeight(); 15 16 if(TryWeight>=0){ 17 dp[i][j] = Math.max(dp[i-1][j], dp[i][TryWeight]+items.get(i).getValue()); 18 trace[i][j] = (dp[i][TryWeight]+items.get(i).getValue())>=dp[i-1][j]?i+1:trace[i-1][j]; 19 }else{ 20 dp[i][j] = dp[i-1][j]; 21 trace[i][j] = trace[i-1][j]; 22 } 23 } 24 }
标签:
原文地址:http://www.cnblogs.com/whaochen205/p/5838486.html