标签:
我们假设以一组连续空间存储树的结点,同时在每个结点中,附设一个指示器指向其双亲结点到链表中的位置。也就是说每个结点除了知道自己之外还需要知道它的双亲在哪里。
它的结构特点是如图所示:
以下是我们的双亲表示法的结构定义代码:
/*树的双亲表示法结点结构定义 */ #define MAXSIZE 100 typedef int ElemType; //树结点的数据类型,暂定为整形 typedef struct PTNode //结点结构 { ElemType data; //结点数据 int parent; //双亲位置 }PTNode; typedef struct { PTNode nodes[MAXSIZE]; //结点数组 int r,n; //根的位置和结点数 }PTree;
孩子表示法
换一种不同的考虑方法。由于每个结点可能有多棵子树,可以考虑使用多重链表,即每个结点有多个指针域,其中每个指针指向一棵子树的根结点,我们把这种方法叫做多重链表表示法。不过树的每个结点的度,也就是它的孩子个数是不同的。所以可以设计两种方案来解决。
方案一:
一种是指针域的个数就等于树的度(树的度是树的各个结点度的最大值)
其结构如图所示:
不过这种结构由于每个结点的孩子数目不同,当差异较大时,很多结点的指针域就都为空,显然是浪费空间的,不过若树的各结点度相差很小时,那就意味着开辟的空间都被利用了,这时这种缺点反而变成了优点。
方案二:
第二种方案是每个结点指针域的个数等于该结点的度,我们专门取一个位置来存储结点指针域的个数。
其结构如图所示:
这种方法克服了浪费空间的缺点,对空间的利用率是很高了,但是由于各个结点的链表是不相同的结构,加上要维护结点的度的数值,在运算上就会带来时间上的损耗。
能否有更好的方法呢,既可以减少空指针的浪费,又能是结点结构相同。
说到这大家肯定就知道是有的麦,那就是孩子表示法。
具体办法是,把每个结点的孩子排列起来,以单链表做存储结构,则n个结点有n个孩子链表,如果是叶子结点则此单链表为空。然后n个头指针有组成一个线性表,采用顺序存储结构,存放进入一个一维数组中。
为此,设计两种结点结构,
一个是孩子链表的孩子结点,如下所示:
其中child是数据域,用来存储某个结点在表头数组中的下标。next是指针域,用来存储指向某结点的下一个孩子结点的指针。
另一个是表头结点,如下所示:
其中data是数据域,存储某结点的数据信息。firstchild是头指针域,存储该结点的孩子链表的头指针。
以下是孩子表示法的结构定义代码:
/*树的孩子表示法结点结构定义 */ #define MAXSIZE 100 typedef int ElemType; //树结点的数据类型,暂定为整形 typedef struct CTNode //孩子结点 { int child; struct CTNode *next; }*ChildPtr; typedef struct //表头结构 { ElemType data; ChildPtr firstchild; }CTBox; typedef struct //树结构 { CTBox nodes[MAXSIZE]; //结点数组 int r,n; //根结点的位置和结点数 }CTree;
3、孩子兄弟表示法
我们发现,任意一颗树,它的结点的第一个孩子如果存在就是的,它的右兄弟如果存在也是唯一的。因此,我们设置两个指针,分别指向该结点的第一个孩子和此结点的右兄弟。
其结点结构如图所示:
以下是孩子兄弟表示法的结构定义代码:
/*树的孩子兄弟表示法结构定义 */ typedef struct CSNode { ElemType data; struct CSNode *firstchild, *rightsib; }CSNode, *CSTree;
二叉树的定义就不赘述了,这里提供二叉树几种常见的算法:
#include <iostream> #include <vector> #include <queue> using namespace std; struct TreeNode { int val; TreeNode* left; TreeNode* right; TreeNode(int val) :val(val) {}; }; //建立二叉树 void CreateTree(TreeNode* &T,int a[],int len,int index) { if (index > len) return; TreeNode* root = new TreeNode(a[index]); root->left = NULL; root->right = NULL; CreateTree(root->left, a, len, index * 2 + 1); CreateTree(root->right, a, len, index * 2 + 2); } TreeNode* CreateTree_2(int a[], int len, int index) { if (index > len) return NULL; TreeNode* root = new TreeNode(a[index]); root->left = CreateTree_2(a, len, 2 * index + 1); root->right = CreateTree_2(a, len, 2 * index + 2); return root; } //先序遍历 void PreOrder(TreeNode* root) { if (!root) return; else { cout << root->val; PreOrder(root->left); PreOrder(root->right); } return; } //中序遍历 void InOrder(TreeNode* root) { if (!root) return; else { InOrder(root->left); cout << root->val; InOrder(root->right); } return; } //后序遍历 void PostOrder(TreeNode* root) { if (!root) return; else { PostOrder(root->left); PostOrder(root->right); cout << root->val; } return; } //层序遍历并计算宽度 int LevelOrder(TreeNode* root) { if (root == NULL) return; queue<TreeNode*> q1; q1.push(root); int cursize = 1,maxsize=1; while (!q1.empty()) { TreeNode* tmp = q1.front(); q1.pop(); cursize--; cout << tmp->val; if (tmp->left != NULL) q1.push(tmp->left); if (tmp->right != NULL) q1.push(tmp->right); if (cursize == 0) { cursize = q1.size(); maxsize = cursize > maxsize ? cursize : maxsize; } } return maxsize; } //计算树的高度 int HeightTree(TreeNode* root) { if (root == NULL) return 0; int left = 0, right = 0; if (root->left != NULL) left = HeightTree(root->left) + 1; if (root->right != NULL) right = HeightTree(root->right) + 1; return left > right ? left : right; } //根据前序和中序重建二叉树 TreeNode* RebuildTree(vector<int>& preorder, vector<int>::iterator& i, vector<int>& inorder, vector<int>::iterator start, vector<int>::iterator end) { if (preorder.size() == 0 || inorder.size() == 0 || start == end) return NULL; vector<int>::iterator j = find(start, end, *i); if (j == end) return NULL; TreeNode* root = new TreeNode(*i++); root->left = RebuildTree(preorder, i, inorder, start, j); root->right = RebuildTree(preorder, i, inorder, j + 1, end); return root; } TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) { auto i = preorder.begin(); return RebuildTree(preorder, i, inorder, inorder.begin(), inorder.end()); } //
关于图的搜索有两种:广度优先(bfs)深度优先 (dfs)。
以下图为例: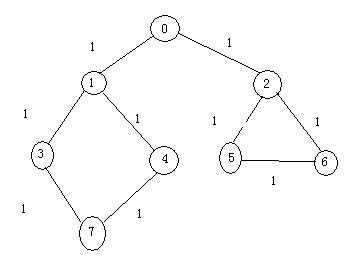
深度优先的基本思想简单说就是搜到底,重新搜。从v0为起点进行搜索,如果被访问过,则做一个标记,直到与v0想连通的点都被访问一遍,如果这时,仍然有点没被访问,可以从中选一个顶点,进行再一次的搜索,重复上述过程,所以深度优先的过程也是递归的过程。
深度优先访问的结果是:0->1->3->7->4->2->5->6
广度优先的基本思想是,从顶点v0出发,访问与v0相邻的点,访问结束后,再从这些点出发,继续访问,直到访问结束为止。标记被访问过的点同深搜一下,不过,广度优先一般需要用到队列。
上图广度优先的结果:0->1->2->3->4->5->6->7
#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<queue> #include<stack> #define maxn 100 using namespace std; typedef struct { int edges[maxn][maxn]; //邻接矩阵 int n; //顶点数 int e; //边数 }MGraph; bool vis[maxn]; //标记顶点是否被访问过 void createGraph(MGraph &G) //用引用做参数 { int i,j; int s,t; //存储顶点的编号 int v; //存储边的权值 for(i=0;i<G.n;i++) //初始化 { for(j=0;j<G.n;j++) { G.edges[i][j] = 0; } vis[i] = false; } for(i = 0;i<G.e;i++) //对邻接矩阵的边赋值 { scanf("%d%d%d",&s,&t,&v); //输入边顶点的编号以及权值 G.edges[s][t] = v; } } void dfs(MGraph G,int v) { int i; printf("%d ",v); //访问结点v vis[v] = true; for(int i = 0;i<G.n;i++) //访问与v相邻且未被访问过的结点 { if(G.edges[v][i]!=0&&vis[i]==false) { dfs(G,i); } } } void dfs1(MGraph G,int v) //非递归实现(用到了栈,其实在递归的实现过程,仍是用到了栈,所以。。。) { stack<int> s; printf("%d",v); //访问初始的结点 vis[v]=true; s.push(v); //入栈 while(!s.empty()) { int i,j; i=s.top(); //取栈顶顶点 for(j=0;j<G.n;j++) //访问与顶点i相邻的顶点 { if(G.edges[i][j]!=0&&vis[j]==false) { printf("%d ",j); //访问 vis[j]=true; s.push(j); //访问完后入栈 break; //找到一个相邻未访问的顶点,访问之后跳出循环 } } if(j==G.n) //如果与i相邻的顶点都被访问过,则将顶点i出栈 s.pop(); } } void bfs(MGraph G,int v) { queue<int> Q; printf("%d",v); vis[v] = true; Q.push(v); while(!Q.empty()) { int i,j; i = Q.front(); //取队首顶点 Q.pop(); for(j=0;j<G.n;j++) //广度遍历 { if(G.edges[i][j]!=0&&vis[j]==false) { printf("%d",j); vis[j]=true; Q.push(j); } } } } int main() { int n,e; //建图的顶点数和边数 while(scanf("%d%d",&n,&e)==2&&n>0) { MGraph G; G.n = n; G.e = e; createGraph(G); dfs(G,0); printf("\n"); // dfs1(G,0); // printf("\n"); // bfs(G,0); // printf("\n"); } return 0; } /*测试数据: 8 9 0 1 1 1 3 1 1 4 1 3 7 1 4 7 1 0 2 1 2 5 1 5 6 1 2 6 1 */
标签:
原文地址:http://www.cnblogs.com/LUO77/p/5839273.html