标签:
决策树学习基本算法
输入:训练集;
???? 属性集.
过程:函数
1: 生成结点node;
2: if 中样本全属于同一类别 then
3: ????将node标记为类叶结点; return
4: end if
5: if 中样本在上取值相同 then
6: 将node标记为叶结点,其类别标记为中样本数最多的类; return
7: end if
8: 从中选择最优化分属性
9: for 的每一个值 do
10: 为node生成一个分支; 令表示中在上取值为的样本子集;
11:???? if 为空 then
12:???? 将分支结点标记为叶结点,其类别标记为中样本最多的类; return
13:???? else
14:????????以为分支结点
15: ???? end if
16: end for
输出:以node为根结点的一棵决策树
Table3 天气数据集
No. | outlook | temperature | humidity | windy | play |
1 | sunny | 85.0 | 85.0 | FALSE | no |
2 | sunny | 80.0 | 90.0 | TRUE | no |
3 | overcast | 83.0 | 86.0 | FALSE | yes |
4 | rainy | 70.0 | 96.0 | FALSE | yes |
5 | rainy | 68.0 | 80.0 | FALSE | yes |
6 | rainy | 65.0 | 70.0 | TRUE | no |
7 | overcast | 64.0 | 65.0 | TRUE | yes |
8 | sunny | 72.0 | 95.0 | FALSE | no |
9 | sunny | 69.0 | 70.0 | FALSE | yes |
10 | rainy | 75.0 | 80.0 | FALSE | yes |
11 | sunny | 75.0 | 70.0 | TRUE | yes |
12 | overcast | 72.0 | 90.0 | TRUE | yes |
13 | overcast | 81.0 | 75.0 | FALSE | yes |
14 | rainy | 71.0 | 91.0 | TRUE | no |
?
信息增益
假定当前样本集合中第类样本所占的比例为,则的信息熵定义为:
????假定离散属性有个可能的取值,若使用来对样本集合进行划分,则会产生个分支结点,其中第个分支结点包含了中所有在属性上取值为的样本,记为. 计算出的信息熵,再考虑到不同的分支结点所包含的样本数不同,给分支结点赋予权重,即样本数越多的分支结点的影响越大,于是可计算出用属性对样本集进行划分所获得的"信息增益"
ID3算法选择属性.
以天气数据集为例,在决策树学习开始时,根结点包含中的所有样例,其中正例占,反例占.于是可计算出根结点的信息熵为
我们要计算出当前属性集合{outlook, temperature, humidity, windy}中每个属性的信息增益。以属性"outlook"为例,它有3个可能的取值:{sunny, overcast, rainy}.若使用该属性对D进行划分,则可得到3个子集,分别记为:(outlook = sunny),(outlook = overcast),(outlook = rainy).
子集包含编号为{1,2,8,9,11}的5个样例,其中正例占,反例占包含编号为{3,7,12,13}的4个样例,其中正、反例分别占,反例占包含编号为{4,5,6,10,14}的5个样例,其中正、反例分别占.根据公式计算出用"outlook"划分之后所获得的3个分支结点的信息熵为
可计算出属性"outlook"的信息增益为
类似的,我们可计算出其他属性的信息增益。
对连续属性"temperature",C4.5采用二分法对连续属性进行处理。
首先找出训练样本在"temperature"属性上的最大和最小值,在最大和最小值限定的取值区间上设置多个等分断点;分别计算以这些断点为分裂点的信息增益值,并比较;具有最大信息增益的断点及最佳分裂点,自该分裂点把整个取值区间划分为两部分,相应的依据记录在该属性上的取值,也将该记录集划分为两部分。
以64.5为例,属性"temperature"可看做有两个取值
?
增益率
信息增益准则对可取值数目较多的属性有所偏好,为减少这种偏好可能带来的不利影响,C4.5算法使用"增益率"来选择最优划分属性. 采用相同的符号表示,增益率定义为:
,
其中
称为属性的"固有值"。属性的可能取值数目越多(即越大),则值通常会越大。
对天气数据集,以属性"outlook"为例,
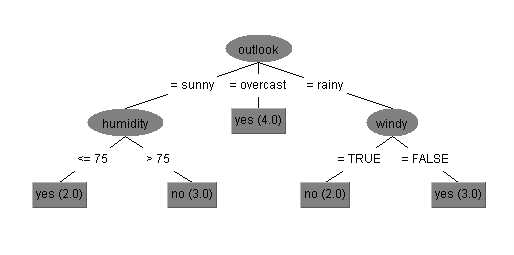
图 在天气数据集上基于信息增益率生成的决策树
?
基尼指数
CART决策树使用"基尼指数"来选择划分属性。采用相同的符号,数据集D的纯度可用基尼值来度量:
?
反映了从数据集中随机抽取两个样本,其类别标记不一致的概率。因此,越小,则数据集D的纯度越高。
属性a的基尼指数定义为
最优划分属性
剪枝处理
决策树剪枝的基本策略有"预剪枝"和"后剪枝"。预剪枝是指在决策树生成过程中,对每个结点在划分前先进行估计,若当前结点的划分不能带来决策树泛化性能提升,则停止划分并将当前结点标记为叶结点;后剪枝则是先从训练集生成一棵完整的决策树,然后自底向上地对非叶结点进行考察,若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升,则将该子树替换为非叶结点。
预剪枝使得决策树的很多分支都没有"展开",这不仅降低了过拟合的风险,还显著减少了决策树的训练时间开销和测试时间开销。但另一方面,有些分支的当前划分虽不能提升泛化性能、甚至可能导致泛化性能暂时下降,但在其基础上进行的后续划分却有可能导致性能显著提高;预剪枝基于"贪心"本质禁止这些分支展开,给预剪枝决策树带来了欠拟合的风险。
一般情形下,后剪枝决策树的欠拟合风险很小,泛化性能往往优于预剪枝决策树。但后剪枝过程是在生成完全决策树之后进行的,并且要自底向上地对树中的所有非叶结点进行逐一考察,因此其训练时间开销比未剪枝决策树和预剪枝决策树都要大得多。
?
缺失值处理
将信息增益的计算式推广为
其中表示D中在属性上没有缺失值的样本子集,表示中在属性a上取值为的样本子集,对属性a,表示无缺失值样本所占的比例,表示无缺失值样本中第类所占的比例,则表示无缺失值样本中在属性a上取值为的样本所占的比例。
?
在决策树学习开始阶段,根结点中各样本的权重初始化为1.
随机森林
简单地说,随机森林就是用随机的方式建立一个森林,森林里面有很多的决策树组成,随机森林的每一棵决策树之间是没有关联的。在得到森林之后,当有一个新的输入样本进入的时候,就让森林中的每一棵决策树分别进行一下判断,看看这个样本应该属于哪一类(对于分类算法),然后看看哪一类被选择最多,就预测这个样本为那一类。
随机森林主要包括4个部分:随机选择样本;随机选择特征;构建决策树;随机森林投票分类。
给定一个训练样本集,数量为N,使用有放回采样到N个样本,构成一个新的训练集。注意这里是有放回的采样,所以会采样到重复的样本。详细来说,就是采样N次,每次采样一个,放回,继续采样。即得到了N个样本。然后我们把这个样本集作为训练集,进入下面的一步。
从总量为M的特征向量中,随机选择m个特征,其中m可以等于sqrt(M),然后计算m个特征的增益,选择最优特征(属性)。注意,这里的随机选择特征是无放回的选择!
有了上面随机产生的样本集,我们就可以使用一般决策树的构建方法,得到一棵分类(或者预测)的决策树。需要注意的是,在计算节点最优分类特征的时候,我们要使用上面的随机选择特征方法。而选择特征的标准可以是我们常见的Information Gain(ID3) 或者 Gain Ratio(C4.5)。
??通过上面的三步走,我们可以得到一棵决策树,我们可以重复这样的过程T次,就得到了T棵决策树。然后来了一个测试样本,我们就可以用每一棵决策树都对它分类一遍,得到了T个分类结果。这时,我们可以使用简单的投票机制,或者该测试样本的最终分类结果。
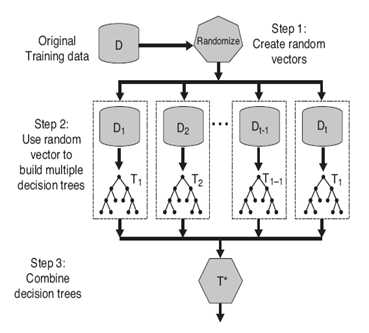
按照1生成t个决策树之后,对于每个新的测试样例,综合多个决策树的分类结果来作为随机森林的分类结果。
? (1)目标特征为数字类型:取t个决策树的平均值作为分类结果。
? (2)目标特征为类别类型:少数服从多数,取单棵树分类结果最多的那个类别作为整个随机森林的分类结果。
?
??优点:
它能够处理很高维度(feature很多)的数据,并且不用做特征选择;
由于随机选择样本导致的每次学习决策树使用不同训练集,所以可以一定程度上避免过拟合;
??缺点:
随机森林已经被证明在某些噪音较大的分类或回归问题上会过拟合;
对于有不同级别的属性的数据,级别划分较多的属性会对随机森林产生更大的影响,所以随机森林在这种数据上产出的属性权值是不可信的
标签:
原文地址:http://www.cnblogs.com/iamxyq/p/5841005.html