标签:
题目:给定二叉树的前序遍历和中序遍历,生成二叉树。
Example:
前序遍历数组:preArr[]:{1,2,4,5,3,6,7}
中序遍历数组:inArr[]:{4,2,5,1,6,3,7}
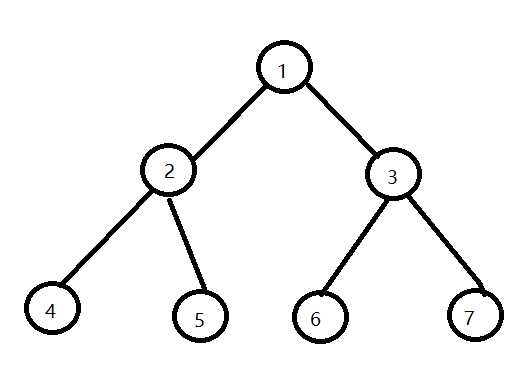
生成的二叉树如下图:
解题思路:
由二叉树的前序变量性质可知:preArr[0] 是数组的根节点,有根据二叉树的中序遍历的性质可知,{4,2,5}是二叉树的左子树,{6,3,7}在右子树上,重复执行该操作就构造出了二叉树
public class Solution {
public TreeNode reConstructBinaryTree(int[] pre, int[] in) {
TreeNode root = new TreeNode(pre[0]);//前序的第一个数定为根
int len = pre.length;
//当只有一个数的时候
if (len == 1) {
root.left = null;
root.right = null;
return root;
}
//找到中序中的根位置
int rootval = root.val;
int i;
for (i = 0; i < len; i++) {
if (rootval == in[i])
break;
}
//创建左子树
if (i > 0) {
int[] pr = new int[i];
int[] ino = new int[i];
for (int j = 0; j < i; j++) {
pr[j] = pre[j + 1];
}
for (int j = 0; j < i; j++) {
ino[j] = in[j];
}
root.left = reConstructBinaryTree(pr, ino);
} else {
root.left = null;
}
//创建右子树
if (len - i - 1 > 0) {
int[] pr = new int[len - i - 1];
int[] ino = new int[len - i - 1];
for (int j = i + 1; j < len; j++) {
ino[j - i - 1] = in[j];
pr[j - i - 1] = pre[j];
}
root.right = reConstructBinaryTree(pr, ino);
} else {
root.right = null;
}
return root;
}
public static void main(String[] args) {
int[] preArr = {1, 2, 4, 5, 3, 6, 7};
int[] inArr = {4, 2, 5, 1, 6, 3, 7};
Solution s = new Solution();
TreeNode root = s.reConstructBinaryTree(preArr, inArr);
s.postOrder(root);
}
标签:
原文地址:http://www.cnblogs.com/googlemeoften/p/5853280.html