R语言-混合型数据聚类

标签：

利用聚类分析，我们可以很容易地看清数据集中样本的分布情况。以往介绍聚类分析的文章中通常只介绍如何处理连续型变量，这些文字并没有过多地介绍如何处理混合型数据（如同时包含连续型变量、名义型变量和顺序型变量的数据）。本文将利用 Gower 距离、PAM（partitioning around medoids）算法和轮廓系数来介绍如何对混合型数据做聚类分析。

---------------------------------------------------------------------------------------------------

本文主要分为三个部分

• 距离计算
• 聚类算法的选择

• 聚类个数的选择

为了介绍方便，本文直接使用 ISLR 包中的 College 数据集。该数据集包含了自 1995 年以来美国大学的 777 条数据，其中主要有以下几个变量：

• 连续型变量

1. 录取率
2. 学费
3. 新生数量

• 分类型变量

1. 公立或私立院校
2. 是否为高水平院校，即所有新生中毕业于排名前 10% 高中的新生数量占比是否大于 50%

本文中涉及到的R包有：

构建聚类模型之前，我们需要做一些数据清洗工作：

• 录取率等于录取人数除以总申请人数
• 判断某个学校是否为高水平院校，需要根据该学校的所有新生中毕业于排名前 10% 高中的新生数量占比是否大于 50% 来决定

In[5]:

距离计算

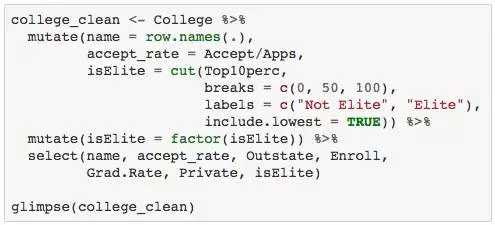
聚类分析的第一步是定义样本之间距离的度量方法，最常用的距离度量方法是欧式距离。然而欧氏距离只适用于连续型变量，所以本文将采用另外一种距离度量方法—— Gower 距离。

1Gower 距离

Gower 距离的定义非常简单。首先每个类型的变量都有特殊的距离度量方法，而且该方法会将变量标准化到[0,1]之间。接下来，利用加权线性组合的方法来计算最终的距离矩阵。不同类型变量的计算方法如下所示：

• 连续型变量：利用归一化的曼哈顿距离
• 顺序型变量：首先将变量按顺序排列，然后利用经过特殊调整的曼哈顿距离
• 名义型变量：首先将包含 k 个类别的变量转换成 k 个 0-1 变量，然后利用 Dice 系数做进一步的计算
• 优点：通俗易懂且计算方便
• 缺点：非常容易受无标准化的连续型变量异常值影响，所以数据转换过程必不可少；该方法需要耗费较大的内存

利用 daisy 函数，我们只需要一行代码就可以计算出 Gower 距离。需要注意的是，由于新生入学人数是右偏变量，我们需要对其做对数转换。daisy函数内置了对数转换的功能，你可以调用帮助文档来获取更多的参数说明。

此外，我们可以通过观察最相似和最不相似的样本来判断该度量方法的合理性。本案例中，圣托马斯大学和约翰卡罗尔大学最相似，而俄克拉荷马科技和艺术大学和哈佛大学差异最大。

Out [ 7 ]

:

Out [ 8 ]:

聚类算法的选择

现在我们已经计算好样本间的距离矩阵，接下来需要选择一个合适的聚类算法，本文采用 PAM（partioniong around medoids）算法来构建模型,PAM 算法的主要步骤：

1. 随机选择 k 个数据点，并将其设为簇中心点
2. 遍历所有样本点，并将样本点归入最近的簇中
3. 对每个簇而言，找出与簇内其他点距离之和最小的点，并将其设为新的簇中心点
4. 重复第2步，直到收敛

该算法和 K-means 算法非常相似。事实上，除了中心点的计算方法不同外，其他步骤都完全一致 。

• 优点：简单易懂且不易受异常值所影响
• 缺点：算法时间复杂度为 O(n2)

聚类个数的选择

我们将利用轮廓系数来确定最佳的聚类个数，轮廓系数是一个用于衡量聚类离散度的内部指标，该指标的取值范围是[-1,1]，其数值越大越好。通过比较不同聚类个数下轮廓系数的大小，我们可以看出当聚类个数为 3 时，聚类效果最好。

聚类结果解释

1描述统计量

聚类完毕后，我们可以调用 summary 函数来查看每个簇的汇总信息。从这些汇总信息中我们可以看出：簇1主要是中等学费且学生规模较小的私立非顶尖院校，簇2主要是高收费、低录取率且高毕业率的私立顶尖院校，而簇3则是低学费、低毕业率且学生规模较大的公立非顶尖院校。

PAM 算法的另一个优点是各个簇的中心点是实际的样本点。从聚类结果中我们可以看出，圣弗朗西斯大学是簇1 的中心点，巴朗德学院是簇2 的中心点，而密歇根州州立大学河谷大学是簇3 的中心点。

2可视化方法

t-SNE 是一种降维方法，它可以在保留聚类结构的前提下，将多维信息压缩到二维或三维空间中。借助t-SNE我们可以将 PAM 算法的聚类结果绘制出来，有趣的是私立顶尖院校和公立非顶尖院校这两个簇中间存在一个小聚类簇。

进一步探究可以发现，这一小簇主要包含一些竞争力较强的公立院校，比如弗吉尼亚大学和加州大学伯克利分校。虽然无法通过轮廓系数指标来证明多分一类是合理的，但是这 13 所院校的确显著不同于其他三个簇的院校。

Out[ 25 ]

转自：http://mp.weixin.qq.com/s?__biz=MzA5NDQ3MDI4NA==&mid=2658610279&idx=1&sn=c913e162de03343a4f89410c18e503a9&scene=1&srcid=09093EVj3DjQk3Jr0UoGqBNT#rd

原文链接：https://dpmartin42.github.io/blogposts/r/cluster-mixed-types

R语言-混合型数据聚类

标签：

原文地址：http://www.cnblogs.com/payton/p/5856113.html