标签:
首先,我们看看前序、中序、后序遍历的特性:
前序遍历:
1.访问根节点
2.前序遍历左子树
3.前序遍历右子树
中序遍历:
1.中序遍历左子树
2.访问根节点
3.中序遍历右子树
后序遍历:
1.后序遍历左子树
2.后序遍历右子树
3.访问根节点
一、已知前序、中序遍历,求后序遍历
前序遍历: GDAFEMHZ
中序遍历: ADEFGHMZ
算法流程:
1 确定根,确定左子树,确定右子树。
2 在左子树中递归。
3 在右子树中递归。
4 打印当前根。
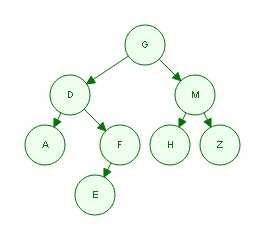
后序遍历顺序为:AEFDHZMG
编程实现:
#include <iostream> #include <fstream> #include <string> struct TreeNode { struct TreeNode* left; struct TreeNode* right; char elem; }; void BinaryTreeFromOrderings(char* inorder, char* preorder, int length) { if(length == 0) { //cout<<"invalid length"; return; } TreeNode* node = new TreeNode;//Noice that [new] should be written out. node->elem = *preorder; int rootIndex = 0; for(;rootIndex < length; rootIndex++) { if(inorder[rootIndex] == *preorder) break; } //Left BinaryTreeFromOrderings(inorder, preorder +1, rootIndex); //Right BinaryTreeFromOrderings(inorder + rootIndex + 1, preorder + rootIndex + 1, length - (rootIndex + 1)); cout<<node->elem<<endl; return; } int main(int argc, char* argv[]) { printf("Hello World!\n"); char* pr="GDAFEMHZ"; char* in="ADEFGHMZ"; BinaryTreeFromOrderings(in, pr, 8); printf("\n"); return 0; }
二、已知后序、中序遍历,求前序遍历
中序遍历: ADEFGHMZ
后序遍历: AEFDHZMG
算法流程:
1 确定根,确定左子树,确定右子树。
2 在左子树中递归。
3 在右子树中递归。
4 打印当前根。
那么,前序遍历: GDAFEMHZ
编程实现:
#include <iostream> #include <fstream> #include <string> struct TreeNode { struct TreeNode* left; struct TreeNode* right; char elem; }; TreeNode* BinaryTreeFromOrderings(char* inorder, char* aftorder, int length) { if(length == 0) { return NULL; } TreeNode* node = new TreeNode;//Noice that [new] should be written out. node->elem = *(aftorder+length-1); std::cout<<node->elem<<std::endl; int rootIndex = 0; for(;rootIndex < length; rootIndex++)//a variation of the loop { if(inorder[rootIndex] == *(aftorder+length-1)) break; } node->left = BinaryTreeFromOrderings(inorder, aftorder , rootIndex); node->right = BinaryTreeFromOrderings(inorder + rootIndex + 1, aftorder + rootIndex , length - (rootIndex + 1)); return node; } int main(int argc, char** argv) { char* af="AEFDHZMG"; char* in="ADEFGHMZ"; BinaryTreeFromOrderings(in, af, 8); printf("\n"); return 0; }
标签:
原文地址:http://www.cnblogs.com/sweetyu/p/5867939.html