标签:
tarjan——求解有向图强连通分量。这个算法在本人的一篇blog中有介绍,这里就不赘述了。贴上介绍tarjan的的blog链接:http://www.cnblogs.com/Maki-Nishikino/p/5866191.html
那么接下来说说SPFA:
SPFA全称Shortest Path Faster Algorithm,用于求解单源最短路。既然名字中有“Faster”,那它就一定有过人之处,事实上它也的确比Dijkstra和Bellman-Ford更高效。
它的思路大致如下:
1、先用邻接表把图存下来,并且规定一个数组d,d[i]表示起点到i的最短路程;
2、建立一个队列,将起点放入队列;
3、对队首元素执行松弛操作,遍历所有以队首元素为起点的边,如果被遍历的边可以使到被遍历的边的终点的路径变短,那么就更新这个最短路径,并把被遍历的边的终点放到队尾;
4、每完成一次松弛,就令队首元素出队,重复2,直到队列里没有元素。
原谅博主懒得贴伪代码,我就直接讲题了,反正题解里也有模板#手动滑稽
原题链接(来自bzoj):http://www.lydsy.com/JudgeOnline/problem.php?id=1179
题目描述:
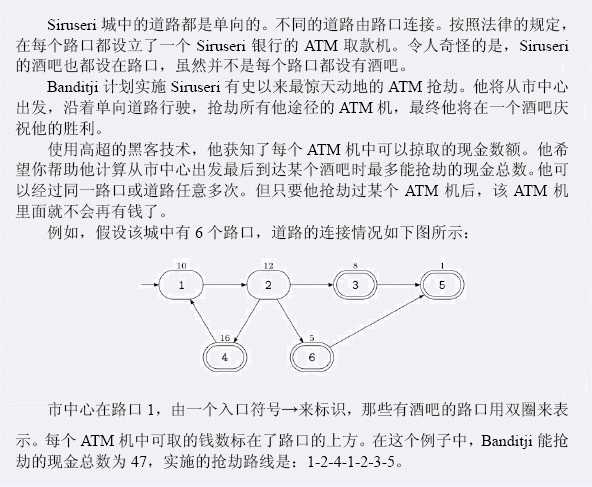
输入:
第一行包含两个整数N、M。N表示路口的个数,M表示道路条数。接下来M行,每行两个整数,这两个整数都在1到N之间,第i+1行的两个整数表示第i条道路的起点和终点的路口
编号。接下来N行,每行一个整数,按顺序表示每个路口处的ATM机中的钱数。接下来一行包含两个整数S、P,S表示市中心的编号,也就是出发的路口。P表示酒吧数目。接下来
的一行中有P个整数,表示P个有酒吧的路口的编号。
输出:
输出一个整数,表示Banditji从市中心开始到某个酒吧结束所能抢劫的最多的现金总数。
样例输入:
6 7
1 2
2 3
3 5
2 4
4 1
2 6
6 5
10
12
8
16
1
5
1 4
4
3
5
6
样例输出:
47
数据范围:
50%的输入保证N, M<=3000。所有的输入保证N, M<=500000。每个ATM机中可取的钱数为一个非负整数且不超过4000。输入数据保证你可以从市中心沿着Siruseri的单向的道路到达其中的至少一个酒吧。
对于这道题,我们考虑先用tarjan求出它的所有强连通分量,再把同嘤一个强连通分量上的ATM机的钱加起来,让一个强连通分量上的点缩成一个点。然后以市中心s为起点,用SPFA跑出s到其他点的最长(最有价值)路,比较酒吧所在点的d值,输出大的即可。
附上代码:

1 #include<stdio.h> 2 #include<algorithm> 3 #include<string.h> 4 using namespace std; 5 struct node 6 { 7 int v; 8 int next; 9 int w; 10 }; 11 int n,m; 12 node e[500010],map[500010];//邻接表存图 13 int st[500010],head[500010],cnt; 14 int atm[500010],money[500010]; 15 int d[500010],q[500010];//最短路径&SPFA要用的队列 16 void build(int a,int b) 17 { 18 e[++cnt].v=b; 19 e[cnt].next=st[a]; 20 st[a]=cnt; 21 }//建图找强连通分量 22 int stack[500010],top;//tarjan需要的栈 23 int dfn[500010],low[500010],dex;//时间戳(深搜序)、可回溯到的最早栈中时间戳、次序编号 24 bool vis[500010];//tarjan时判断点是否在栈中,SPFA时判断点是否在队列中 25 int color[500010],num;//表示同一强连通分量上的点 26 void tarjan(int x)//tarjan找强连通分量 27 { 28 dfn[x]=++dex; 29 low[x]=dex; 30 vis[x]=true; 31 stack[++top]=x;//当前点入栈 32 int i; 33 for(i=st[x];i!=0;i=e[i].next)//枚举以当前点为起点的边 34 { 35 int temp=e[i].v;//temp为当前被枚举边的终点 36 if(!dfn[temp])//如果当前边终点未被处理 37 { 38 tarjan(temp); 39 low[x]=min(low[x],low[temp]); 40 } 41 else if(vis[temp])low[x]=min(low[x],dfn[temp]); 42 } 43 if(dfn[x]==low[x]) 44 { 45 vis[x]=false; 46 color[x]=++num;//标记当前强连通分量内的点 47 while(stack[top]!=x)//栈顶元素依次出栈 48 { 49 color[stack[top]]=num; 50 vis[stack[top--]]=false; 51 } 52 top--; 53 } 54 } 55 void add()// 把同一强连通分量上的点缩成一个点,把这些点连成一张新图 56 { 57 cnt=0; 58 int i,j; 59 for(i=1;i<=n;i++) 60 { 61 for(j=st[i];j!=0;j=e[j].next) 62 { 63 int temp=e[j].v; 64 if(color[i]!=color[temp]) 65 { 66 map[++cnt].v=color[temp]; 67 map[cnt].next=head[color[i]]; 68 head[color[i]]=cnt; 69 } 70 } 71 72 } 73 } 74 void spfa(int x)//SPFA找最长路 75 { 76 memset(vis,false,sizeof(vis)); 77 int l=1,r=1; 78 q[l]=x;//初始点放入队列 79 vis[x]=true; 80 d[x]=money[x]; 81 while(l<=r) 82 { 83 int u=q[l++]; 84 for(int i=head[u];i!=0;i=map[i].next)//遍历所有以当前点为起点的边 85 { 86 int v=map[i].v; 87 if(d[v]<d[u]+money[v]) 88 { 89 d[v]=d[u]+money[v]; 90 if(vis[v])continue; 91 q[++r]=v;//如果当前拓展的边的终点不在队列里,就把它放入队尾 92 vis[v]=true; 93 } 94 } 95 vis[u]=false; 96 } 97 } 98 int main() 99 { 100 int a,b,i,s,p,o,ans=0; 101 scanf("%d%d",&n,&m); 102 for(i=1;i<=m;i++) 103 { 104 scanf("%d%d",&a,&b); 105 build(a,b); 106 }//建初始图 107 for(i=1;i<=n;i++) 108 { 109 if(!dfn[i])tarjan(i);//找强连通分量 110 } 111 add();//建新图 112 for(i=1;i<=n;i++) 113 { 114 scanf("%d",&atm[i]); 115 money[color[i]]+=atm[i]; 116 } 117 scanf("%d%d",&s,&p); 118 spfa(color[s]);//找单源最短路 119 for(i=1;i<=p;i++) 120 { 121 scanf("%d",&o); 122 ans=max(ans,d[color[o]]);//找到以酒吧为终点的最长路 123 } 124 printf("%d",ans); 125 return 0; 126 }
标签:
原文地址:http://www.cnblogs.com/Maki-Nishikino/p/5868953.html