标签:
匈牙利算法是由匈牙利数学家Edmonds提出的,用增广路径求二分图最大匹配的算法。
听起来高端,其实说白了就是:
假设不存在单相思(单身狗偷偷抹眼泪),在一个同性恋不合法的国家里(不存在任何歧视#正色),有一些男人和女人,他们互相之间存在一些互相爱恋的关系。而匈牙利算法就是要促成尽量多的男女配对。
如下图:
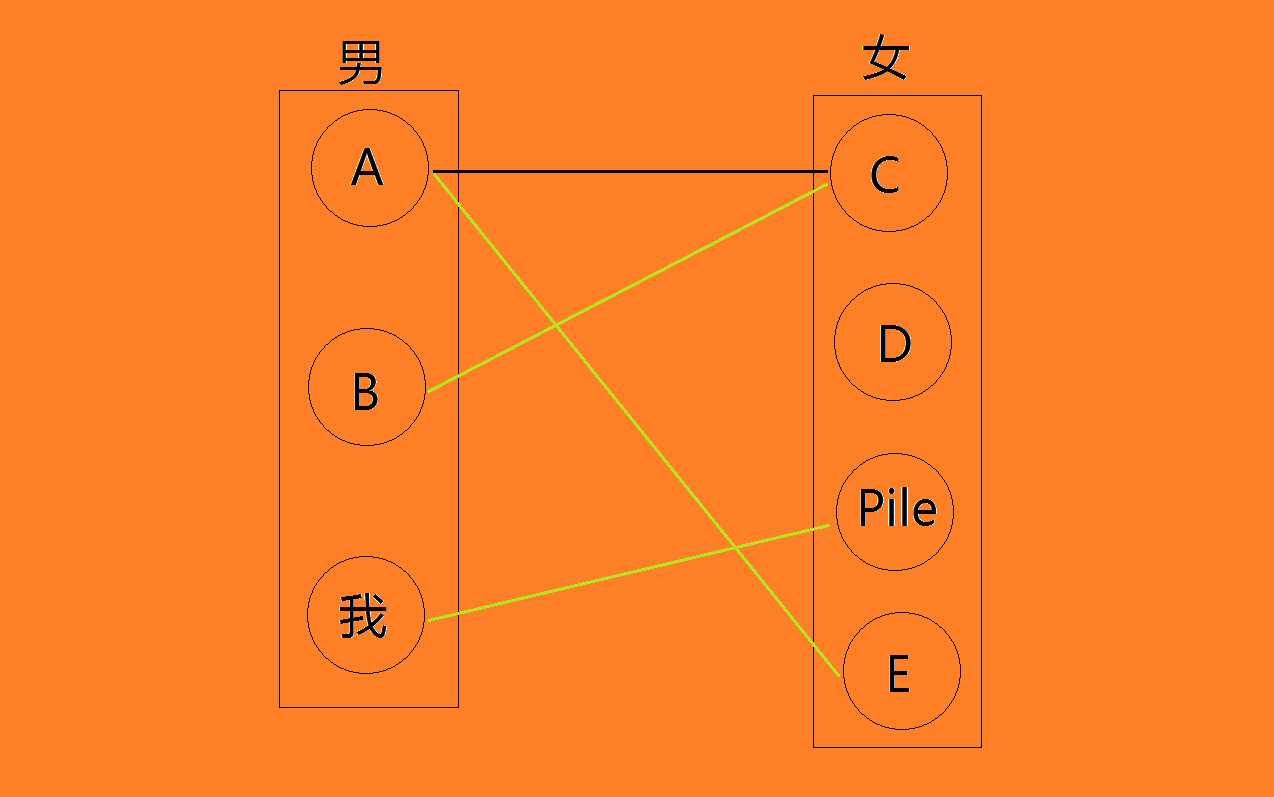
绿色标注的就是这张图的一个最大二分图匹配。
先提一个下面会提到的名词:
增广路:若P是图G中一条连通两个未匹配顶点的路径,并且属于M的边和不属于M的边(即已匹配和待匹配的边)在P上交替出现,则称P为相对于M的一条增广路径。
下面讲讲匈牙利算法的思路:
1、依次从一个部分的每个顶点出发,寻找一条增广路;
2、遍历所有以当前点为起点的边,若找到一条增广路,就更新匹配数,并返回1;否则重复二,直至所有边被遍历;
3、若以当前点为起点的所有边被遍历仍未找到一条可增广路,返回1。
显然,由于寻找增广路的过程需要深搜,所以匈牙利算法是一个基于dfs的算法。思路很简单,所以我就不贴伪代码了才不是因为懒而且还不会写伪代码(划掉),反正hero是裸题,题解里也有模板。
题目描述:
现在电视台有一种节目叫做超级英雄,大概的流程就是每位选手到台上回答主持人的几个问题,然后根据回答问题的多少获得不同数目的奖品或奖金。主持人问题准备了若干道题目,只有当选手正确回答一道题后,才能进入下一题,否则就被淘汰。为了增加节目的趣味性并适当降低难度,主持人总提供给选手几个“锦囊妙计”,比如求助现场观众,或者去掉若干个错误答案(选择题)等等。 这里,我们把规则稍微改变一下。假设主持人总共有m道题,选手有n种不同的“锦囊妙计”。主持人规定,每道题都可以从两种“锦囊妙计”中选择一种,而每种“锦囊妙计”只能用一次。我们又假设一道题使用了它允许的锦囊妙计后,就一定能正确回答,顺利进入下一题。现在我来到了节目现场,可是我实在是太笨了,以至于一道题也不会做,每道题只好借助使用“锦囊妙计”来通过。如果我事先就知道了每道题能够使用哪两种“锦囊妙计”,那么你能告诉我怎样选择才能通过最多的题数吗?
输入:
输入文件的一行是两个正整数n和m(0 < n <1001,0 < m < 1001)表示总共有n中“锦囊妙计”,编号为0~n-1,总共有m个问题。
以下的m行,每行两个数,分别表示第m个问题可以使用的“锦囊妙计”的编号。
注意,每种编号的“锦囊妙计”只能使用一次,同一个问题的两个“锦囊妙计”可能一样。
输出:
第一行为最多能通过的题数p。
样例输入:
5 6
3 2
2 0
0 3
0 4
3 2
3 2
样例输出:
4
数据范围:
0 < n , m < 1001
绝对的裸题,裸得让我怀疑这是我在bzoj上见到的。附上链接→_→http://www.lydsy.com/JudgeOnline/problem.php?id=1191
代码如下:

1 #include<stdio.h> 2 #include<string.h> 3 struct node 4 { 5 int v; 6 int next; 7 }; 8 node e[3010]; 9 int st[3010],cnt; 10 int n,m; 11 bool vis[3010];//判断当遍搜索中某条路径是否被走过 12 int link[3010];//判断左右端点是否相连 link[i]=j代表锦囊i与问题j相连,特别的,当link[i]=0时表示i是一个未盖点 13 void build(int a,int b) 14 { 15 e[++cnt].v=b; 16 e[cnt].next=st[a]; 17 st[a]=cnt; 18 }//建图,问题连向锦囊 19 bool dfs(int x) 20 { 21 int i; 22 for(i=st[x];i!=0;i=e[i].next)//依次枚举当前以左端点为起点的边 23 { 24 if(vis[i])continue;//如果被枚举边已经被访问过,就跳过这条边 25 vis[i]=true; 26 int temp=e[i].v; 27 if(!link[temp]||dfs(link[temp]))//若temp是一个未盖点或从temp对应的问题开始有可增广路,就将temp对应的问题更改为x,并且认为存在从x开始的增广路 28 { 29 link[temp]=x; 30 return true; 31 } 32 } 33 return false; 34 } 35 int main() 36 { 37 scanf("%d%d",&n,&m); 38 int a,b,i,ans=0; 39 for(i=1;i<=m;i++) 40 { 41 scanf("%d%d",&a,&b); 42 build(i,a); 43 build(i,b); 44 }//建图,问题连向锦囊 45 for(i=1;i<=m;i++) 46 { 47 memset(vis,false,sizeof(vis)); 48 if(dfs(i))ans++; 49 else break;//这句一定要加!一定要加!一定要加!说三遍 ←__ ← 最开始没加无限WA,后来意识到这是个闯关游戏,一关没过游戏结束,就不往后做了 50 } 51 printf("%d",ans); 52 return 0; 53 }
标签:
原文地址:http://www.cnblogs.com/Maki-Nishikino/p/5873296.html