标签:
PageRank的主要原理是用链接数量作为搜索排序的一个因子。在互联网上,如果一个网页被很多其他网页所链接,说明它受到普遍的承认和信赖,那么它的排名就高。这就是PageRank的核心思想。举个例子,我们知道一个网页Y的排名应该来自于所有指向这个网特的其他网页X1,X2,.......Xn,的权重之和,如图1所示,Y的网页pageRank=0.001+0.01+0.02+0.05=0.081。
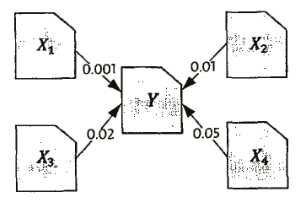
图1 网页排名计算
接下来的问题就是X1,X2,X3,X4的权重分别是多少,如何度量。首先,假定所有的网页排名是相同的,并且根据这个初始值,算出各个网页的第一次迭代排名,然后再根据第一次迭代排名算出第二次的排名,如此迭代下去,知道算法收敛。然而,互联网上的网页数量是巨大的,二维矩阵从网页上讲有网页数量的二次方这么多元素。假如有十亿个网页,那么这个矩阵就有一百亿亿个元素。这么大的矩阵相乘,计算量是巨大的。然而根据网页直接的链接数有限规则,大部分网页之间都是互不引用的。所以二维矩阵中的绝大部分的元素值都是0。所以可以利用稀疏矩阵计算的技巧,大大简化计算量。
假定向量 B=(b1,b2,.....bn)T (1)
为第一,第二,.......第N个网页的网页排名。矩阵

为网页之间链接的数量,其中amn代表第m个网页指向第n个网页的链接数。A是一支的,B是未知的。
假定Bi是第i次迭代的结果,那么
Bi = ABi-1 (2)
初始化B的值,令
B0=(1/N,1/N,........,1/N) (3)
通过(2)简单(但是计算量非常大)的矩阵运算,可以得到B1,B2,......。可以证明Bi最终会收敛,即Bi无限趋近于B,此时B=BA。因此,当两次迭代过程的结果Bi和Bi-1之间的差异非常小,接近于零时,停止迭代运算,算法结束。
由于网页之间连接的数量相比于互联网的规模非常稀疏,因此计算网页的网页排名也需要对零概率或者小概率事件进行平滑处理。网页的排名是一个一维向量,对它的平滑处理只能利用一个小的常数α。这时,公式(2)变成了
Bi = [(α/N)I+(1-α)A]Bi-1 (4)
其中n是网页的数量,α是一个较小的常数,I是单位矩阵。
标签:
原文地址:http://www.cnblogs.com/yangfei2015/p/yangfei2015.html