标签:
问题一:子数组和的最大值:
用f[i]表示以a[i]结尾的最大连续子序列和。i在0~n-1之间,最后比较所有的f[i]找到最大值。对于这样的以为动态规划,可以简化为用一个变量f滚动完成更新。
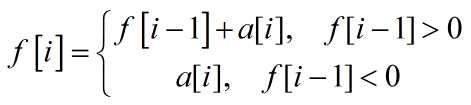
int max_sum(int a[],int n) { int f=a[0]; int max_value=a[0]; for(int i=1;i<n;i++) { if(f<0) f=a[i]; else f=f+a[i]; max_value=max(max_value,f); } return max_value; }
问题二:不相交子数组和之差的最大值。
我们需要将数组分成不相交的两部分,分别求所有可能的两部分的子数组的和的最大值,以及最小值。比如将数组a[0~n]分成a[0~i]与a[i+1~n],我们用f1[i]表示第一部分a[0~i]子数组的最大连续子序列和。f2[i]表示第一部分a[0~i]子数组的最小连续子序列的和。g1[i+1]表示第二部分a[i+1~n]子数组的最大连续子序列和。g2[i+1]表示第二部分a[i+1~n]子数组的最小连续子序列的和。最后对于每一个i,我们求出最大的两部分之差,max(f1[i]-g2[i+1], g1[i+1]-f2[i]);其中f1[i],f2[i],g1[i],g2[i]都是在问题一的基础上求得的result;
int max_diff_sum(int a[],const int n) { vector<int> f1(n);//f1[i]表示a[0~i]子数组中包含的所有连续子序列和的最大值 vector<int> f2(n); vector<int> g1(n); vector<int> g2(n); f1[0]=a[0]; f2[0]=a[0]; int max_left_until=a[0];//表示以a[i]结尾的连续子序列的最大值 int min_left_until=a[0];//表示以a[i]结尾的连续子序列的最小值 for(int i=1;i<n;i++) { if(max_left_until>0) max_left_until+=a[i]; else max_left_until=a[i]; f1[i]=max(f1[i-1],max_left_until); if(min_left_until<0) min_left_until+=a[i]; else min_left_until=a[i]; f2[i]=min(f2[i-1],min_left_until); } g1[n-1]=a[n-1]; g2[n-1]=a[n-1]; int max_right_until=a[n-1]; int min_right_until=a[n-1]; for(int i=n-2;i>=0;i--) { if(max_right_until>0) max_right_until+=a[i]; else max_right_until=a[i]; g1[i]=max(g1[i+1],max_right_until); if(min_right_until<0) min_right_until+=a[i]; else min_right_until=a[i]; g2[i]=min(g2[i+1],min_right_until); } int result=INT_MIN; for(int i=0;i<n-1;i++) { result=max(result,max(f1[i]-g2[i+1],g1[i+1]-f2[i])); } return result; }
问题三:最大连续乘积子串:
对于数组的最大连续乘积的子串,因为乘积可能有正有负,如果前面乘积为负的,刚好a[i]也是负数,就会负负得正。因此我们需要max_until来保存以a[i]结尾的子串的乘积的最大值,用min_until保存以a[i]结尾的子串的乘积的最小值。然后所有的max_until中的最大值为最后的结果。
double max_multi(double a[],int n) { double max_until=a[0]; double min_until=a[0]; double result=a[0]; for(int i=1;i<n;++i) { double temp1=max_until*a[i]; double temp2=min_until*a[i]; max_until=max(max(temp1,temp2),a[i]); min_until=min(min(temp1,temp2),a[i]); result=max(result,max_until); } return result; }
标签:
原文地址:http://www.cnblogs.com/beaglebone/p/5877322.html