标签:
小Hi和小Ho住在P市,P市是一个很大很大的城市,所以也面临着一个大城市都会遇到的问题:交通拥挤。
小Ho:每到周末回家感觉堵车都是一种煎熬啊。
小Hi:平时交通也还好,只是一到上下班的高峰期就会比较拥挤。
小Ho:要是能够限制一下车的数量就好了,不知道有没有办法可以知道交通系统的最大承受车流量,这样就可以限制到一个可以一直很顺畅的数量了。
小Hi:理论上是有算法的啦。早在1955年,T.E.哈里斯就提出在一个给定的网络上寻求两点间最大运输量的问题。并且由此产生了一个新的图论模型:网络流。
小Ho:那具体是啥?
小Hi:用数学的语言描述就是给定一个有向图G=(V,E),其中每一条边(u,v)均有一个非负数的容量值,记为c(u,v)≥0。同时在图中有两个特殊的顶点,源点S和汇点T。
举个例子:
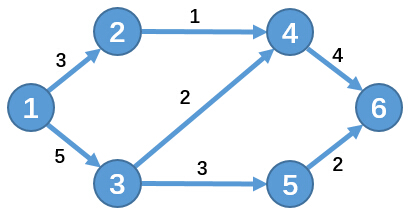
其中节点1为源点S,节点6为汇点T。
我们要求从源点S到汇点T的最大可行流量,这个问题也被称为最大流问题。
在这个例子中最大流量为5,分别为:1→2→4→6,流量为1;1→3→4→6,流量为2;1→3→5→6,流量为2。
小Ho:看上去好像挺有意思的,你让我先想想。
第1行:2个正整数N,M。2≤N≤500,1≤M≤20,000。
第2..M+1行:每行3个整数u,v,c(u,v),表示一条边(u,v)及其容量c(u,v)。1≤u,v≤N,0≤c(u,v)≤100。
给定的图中默认源点为1,汇点为N。可能有重复的边。
第1行:1个整数,表示给定图G的最大流。
6 7 1 2 3 1 3 5 2 4 1 3 4 2 3 5 3 4 6 4 5 6 2
5
分析:最大流关键是求增广路,邻接表存边,便于修改;
代码:
#include <iostream> #include <cstdio> #include <cstdlib> #include <cmath> #include <algorithm> #include <climits> #include <cstring> #include <string> #include <set> #include <map> #include <queue> #include <stack> #include <vector> #include <list> #define rep(i,m,n) for(i=m;i<=n;i++) #define rsp(it,s) for(set<int>::iterator it=s.begin();it!=s.end();it++) #define mod 1000000007 #define inf 0x3f3f3f3f #define vi vector<int> #define pb push_back #define mp make_pair #define fi first #define se second #define ll long long #define pi acos(-1.0) #define pii pair<int,int> #define Lson L, mid, rt<<1 #define Rson mid+1, R, rt<<1|1 const int maxn=5e2+10; using namespace std; ll gcd(ll p,ll q){return q==0?p:gcd(q,p%q);} ll qpow(ll p,ll q){ll f=1;while(q){if(q&1)f=f*p;p=p*p;q>>=1;}return f;} int n,m,k,t,h[maxn],tot,p[maxn],a[maxn],v[maxn][maxn],ans; struct node { int fr,to,nxt,cap,flow; }e[20000<<1]; void add(int x,int y,int z) { e[tot].fr=x; e[tot].to=y; e[tot].nxt=h[x]; e[tot].cap=z; h[x]=tot++; e[tot].fr=y; e[tot].to=x; e[tot].nxt=h[y]; h[y]=tot++; } void max_flow(int s,int t) { ans=0; while(1) { memset(a,0,sizeof a); queue<int>q; q.push(s);a[s]=inf; while(!q.empty()) { int x=q.front(); q.pop(); for(int i=h[x];i!=-1;i=e[i].nxt) { int to=e[i].to,cap=e[i].cap,flow=e[i].flow; if(!a[to]&&cap>flow) { p[to]=i; a[to]=min(a[x],cap-flow); q.push(to); } } if(a[t])break; } if(!a[t])break; for(int now=t;now!=s;now=e[p[now]].fr) { e[p[now]].flow+=a[t]; e[p[now]^1].flow-=a[t]; } ans+=a[t]; } } int main() { int i,j; scanf("%d%d",&n,&m); memset(h,-1,sizeof h); while(m--) { int b,c,d; scanf("%d%d%d",&b,&c,&d); v[b][c]+=d; } rep(i,1,n)rep(j,1,n)if(v[i][j])add(i,j,v[i][j]); max_flow(1,n); printf("%d\n",ans); //system("Pause"); return 0; }
hihocoder网络流一·Ford-Fulkerson算法
标签:
原文地址:http://www.cnblogs.com/dyzll/p/5883240.html