算法分析-堆排序 Heap Sort

标签：

堆排序的是集合了插入排序的单数组操作，又有归并排序的时间复杂度，完美的结合了2者的优点。

堆的定义

　　n个元素的序列{k₁，k₂，…,k_n}当且仅当满足下列关系之一时，称之为堆。

　　情形1：k_i <= k_2i 且k_i <= k_2i+1 （最小化堆或小顶堆）

　　情形2：k_i >= k_2i 且k_i >= k_2i+1 （最大化堆或大顶堆）

　　其中i=1,2,…,n/2向下取整;

若将和此序列对应的一维数组（即以一维数组作此序列的存储结构）看成是一个完全二叉树，则堆的含义表明，完全二叉树中所有非终端结点的值均不大于（或不小于）其左、右孩子结点的值。

由此，若序列{k₁，k₂，…,k_n}是堆，则堆顶元素（或完全二叉树的根）必为序列中n个元素的最小值（或最大值）。

　　例如，下列两个序列为堆，对应的完全二叉树如图：

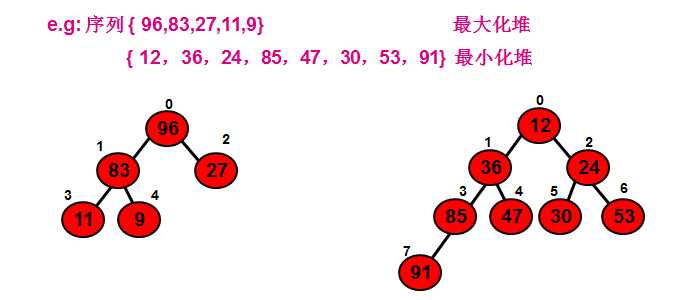
　　若在输出堆顶的最小值之后，使得剩余n-1个元素的序列重又建成一个堆，则得到n个元素的次小值。如此反复执行，便能得到一个有序序列，这个过程称之为堆排序。

　　堆排序（Heap Sort）只需要一个记录元素大小的辅助空间（供交换用），每个待排序的记录仅占有一个存储空间。

堆的存储

　　一般用数组来表示堆，若根结点存在序号0处， i结点的父结点下标就为(i-1)/2。i结点的左右子结点下标分别为2*i+1和2*i+2。

　　（注：如果根结点是从1开始，则左右孩子结点分别是2i和2i+1。）

　　如第0个结点左右子结点下标分别为1和2。

　　如最大化堆如下：

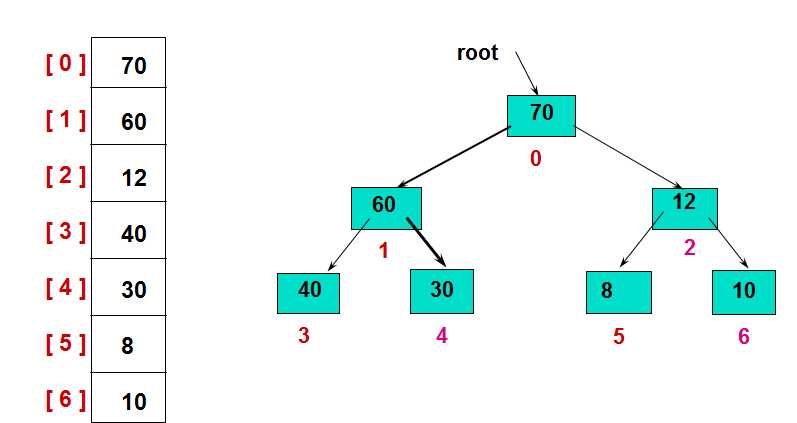
　　左图为其存储结构，右图为其逻辑结构。

堆排序的实现

　　实现堆排序需要解决两个问题：

　　　　1.如何由一个无序序列建成一个堆？

　　　　2.如何在输出堆顶元素之后，调整剩余元素成为一个新的堆？

　　先考虑第二个问题，一般在输出堆顶元素之后，视为将这个元素排除，然后用表中最后一个元素填补它的位置，自上向下进行调整：首先将堆顶元素和它的左右子树的根结点进行比较，把最小的元素交换到堆顶；然后顺着被破坏的路径一路调整下去，直至叶子结点，就得到新的堆。

　　我们称这个自堆顶至叶子的调整过程为“筛选”。

　　从无序序列建立堆的过程就是一个反复“筛选”的过程。

构造初始堆

　　初始化堆的时候是对所有的非叶子结点进行筛选。

　　最后一个非终端元素的下标是[n/2]向下取整，所以筛选只需要从第[n/2]向下取整个元素开始，从后往前进行调整。

　　比如，给定一个数组，首先根据该数组元素构造一个完全二叉树。

　　然后从最后一个非叶子结点开始，每次都是从父结点、左孩子、右孩子中进行比较交换，交换可能会引起孩子结点不满足堆的性质，所以每次交换之后需要重新对被交换的孩子结点进行调整。

进行堆排序

　　有了初始堆之后就可以进行排序了。

　　堆排序是一种选择排序。建立的初始堆为初始的无序区。

　　排序开始，首先输出堆顶元素（因为它是最值），将堆顶元素和最后一个元素交换，这样，第n个位置（即最后一个位置）作为有序区，前n-1个位置仍是无序区，对无序区进行调整，得到堆之后，再交换堆顶和最后一个元素，这样有序区长度变为2。。。

　　不断进行此操作，将剩下的元素重新调整为堆，然后输出堆顶元素到有序区。每次交换都导致无序区-1，有序区+1。不断重复此过程直到有序区长度增长为n-1，排序完成。

堆排序实例

 　　首先，建立初始的堆结构如图：

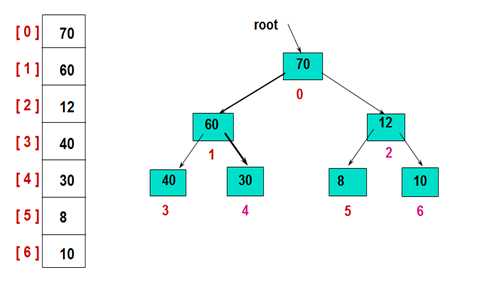
　　然后，交换堆顶的元素和最后一个元素，此时最后一个位置作为有序区（有序区显示为黄色），然后进行其他无序区的堆调整，重新得到大顶堆后，交换堆顶和倒数第二个元素的位置……

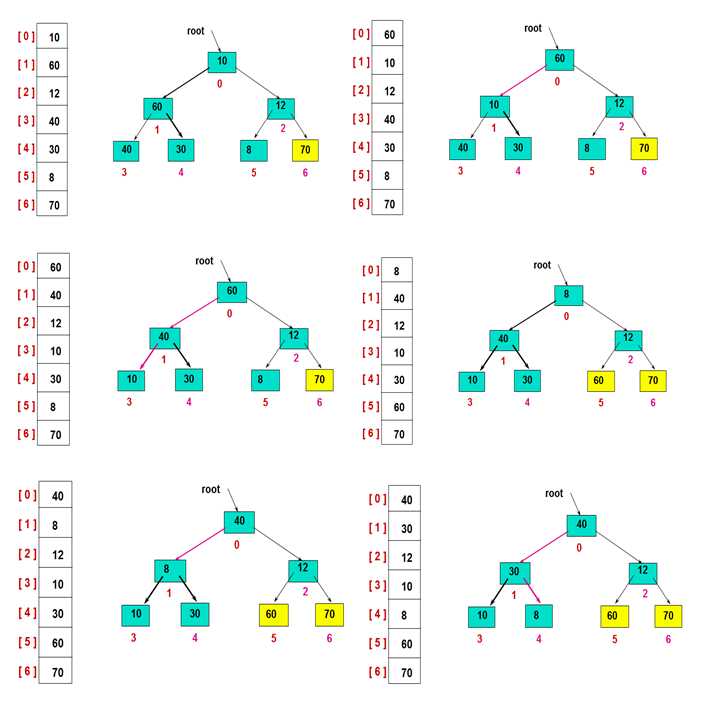
　　重复此过程：

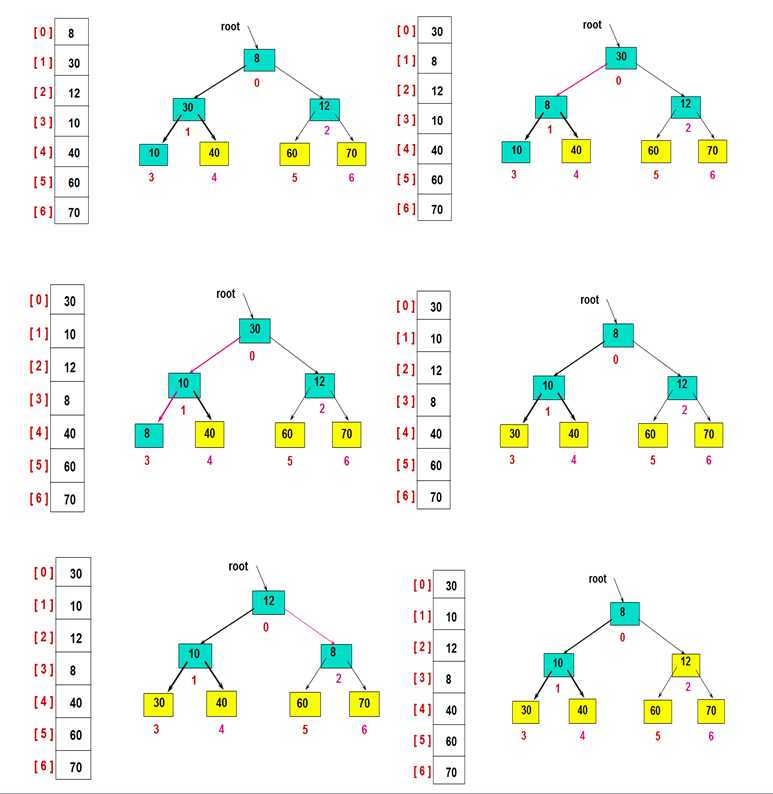
　　最后，有序区扩展完成即排序完成：

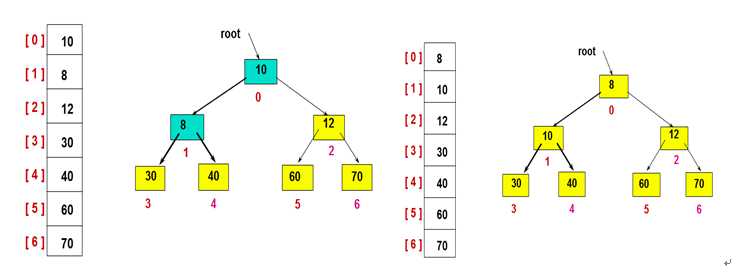
　　由排序过程可见，若想得到升序，则建立大顶堆，若想得到降序，则建立小顶堆。

代码

　　假设排列的元素为整型，且元素的关键字为其本身。

　　因为要进行升序排列，所以用大顶堆。

　　根结点从0开始，所以i结点的左右孩子结点的下标为2i+1和2i+2。

 1 Array.prototype.buildMaxHeap=function(){
 2     for(var i=Math.floor(this.length/2)-1;i>=0;i--){
 3         this.heapAdjust(i,this.length);
 4     }
 5 };
 6 
 7 Array.prototype.swap=function(i,j){
 8     var tmp=this[i];
 9     this[i]=this[j];
10     this[j]=tmp;
11 };
12 
13 Array.prototype.heapSort=function(){
14     this.buildMaxHeap();
15     for(var i=this.length-1;i>0;i--){
16         this.swap(0,i);
17         this.heapAdjust(0,i);
18     }
19 
20     return this;
21 };
22 
23 Array.prototype.heapAdjust=function(i,j){
24     var largest=i;
25     var left=2*i+1;
26     var right=2*i+2;
27 
28     if(left<j&&this[largest]<this[left]){
29         largest=left;
30     }
31 
32     if(right<j&&this[largest]<this[right]){
33         largest=right;
34     }
35 
36     if(largest!=i){
37         this.swap(i,largest);
38         this.heapAdjust(largest,j);
39     }
40 };
41 
42 var a=new Array();
43 [].push.apply(a,[2,4,3,5]);
44 console.log(a.heapSort());

如果对上诉描述还是不清楚，下面给出算法导论里的习题，方面大家一步步更深的理解：

习题一：当A[i]比其两子女都大的时候，调用MAX-HEAPIFY(A,i)的效果是怎么样?

这里的MAX-HEAPIFY对于上诉的heapAdjust,其实没变化的，我们可以看最后的if(largest!=i),才会递归下去，不然不变。这是算法导论里的伪代码：

 习题二:对i>heap-size[A]/2,调用MAX-HEAPIFY(A,i)会怎么样？

分析：我们知道heap-size[A]后面都是排好序的，那heap-size[A]/2的位置便是最后一个非叶子节点，

当i>heap−size[A]/2，结点为叶子结点没有孩子，所以不会有任何改变。

习题三:MAX-HEAPIFY效率虽然高，但是第十行，可能导致某些编译程序产生出低效的代码，请把递归改成迭代：

 1 Max-Heapify(A, i)
 2     while true
 3         l = Left(A, i)
 4         r = Right(A, i)
 5         if l <= A.heap-size and A[l] > A[i]
 6             largest = l
 7         else
 8             largest = i
 9         if r <= A.heap-size and A[r] > A[largest]
10             largest = r
11         if largest != i
12             swap A[i] with A[largest]
13             i = largest
14         else
15             break

整个堆排序的算法：

到此为止，堆排序已经全部讲解完了，我们发现核心的函数就MAX-HEAPTITY,他的时间复杂度其实是和这个二叉树的高度成正比的，我们可以认为是O(lgn).步骤就是先建立一个堆，建完就把第一个元素【最大或者最小】放到最后，如此循环，只到全部排序完毕。

算法分析-堆排序 Heap Sort

标签：

原文地址：http://www.cnblogs.com/huenchao/p/5906193.html