机器学习技法(1)--Linear Support Vector Machine

标签：

线性支持向量机。

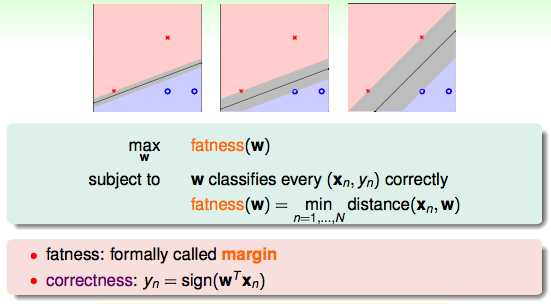
在这种分类问题中，我们需要选一条最“胖”的线，而这条最胖的线就是margin largest的线。

我们的优化目标就是最大化这个margin。也就是在最小化每一个点到这条线的距离。这个距离怎么计算呢？

为了以后不会混淆，w₀就不整合成向量w了，另外取一个新名字b。同样地，x₀=1也就不用塞进x向量里了。

所以得出：h(x)=sign(w^Tx+b)，而距离distance(x,b,w)满足w^Tx‘+b=0

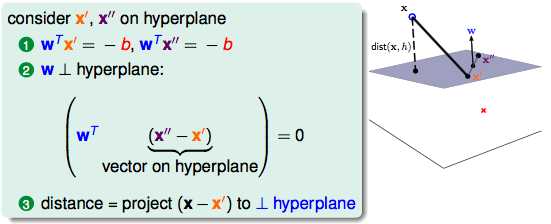
x‘和x‘‘是平面上的两个点，(x‘‘–x‘)是平面上的向量，如果这个平面上的向量和w^T相乘结果是0，那么可以得出w^T是垂直于这个平面的，w^T是这个平面的法向量。

由此可以推导出距离的公式：

这条线还必须得把y进行二元分类，也就是说对于每一个点(x_n,y_n)，这条线都能达到w^Tx_n+b和y_n同号。利用同号的性质将绝对值符号拿掉。

结合之前的公式，我们的优化目标就是：

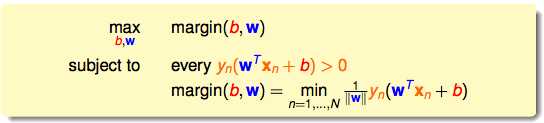
margin(b,w)表示点到线的距离，是由b和w来决定的，我们的目标就是把它最大化，也就是找到使得点到线的距离“最胖”的b和w；

every y_n(w^Tx_n+b)>0表示了每一个点(x_n,y_n)都可以有一个线将它们分开；

再加上一些放缩的技巧，使得y_n(w^Tx_n+b)的值为1，所以就简化了margin(b,w)。

于是margin就被简化成：

限制条件由y_n(w^Tx_n+b)=1放松成y_n(w^Tx_n+b)≥1，下图证明了即使把条件放松了，我们的解不会有什么影响。

我们的最终需要优化的目标为：

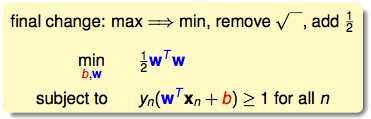
可以先把最大化的一个目标去掉倒数，换成是最小化的目标；为了后面方便计算，再乘个1/2。这个问题叫做标准问题。

先代入几个具体的例子看看情况：

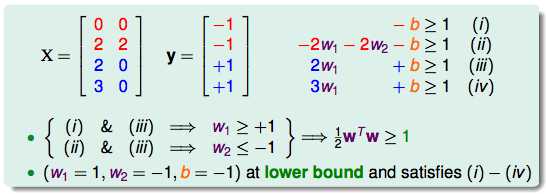
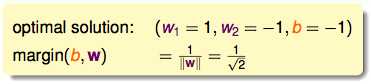
画图之后：

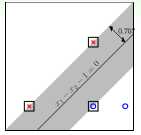
图中带方块的点就是支持向量。只有他们才能决定那条线的样子，其他的点没有也没啥关系。

那么，如果generalize这个题目该怎么解呢？

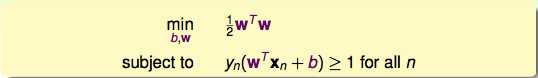
用quadratic programming来解！

补充知识：https://en.wikipedia.org/wiki/Quadratic_programming

Quadratic programming (QP) is a special type of mathematical optimization problem--specifically, the problem of optimizing (either minimzing or maximizing) a quadratic function of several variables subject to linear constraints on these variables.

Problem formulation:

THe quadratic programming problem with n variables and m constraints can be formulated as follows. Given:

A real-valued, n-dimension vector c;

An n×n-dimensional real symmetric matrix Q;

An m×n-dimensional real matrix A;

An m-dimensional real vector b,

the objective of quadratic programming is to find an n-dimensional vector x, that will

minimize 1/2*Q*x^Tx + c^Tx, subject to Ax≤b

the notation Ax≤b means that every entry of the vector Ax is less than or equal to the corresponding entry of the vector b.

将我们想求解的方程式调换成标准的二次规划问题的样式，QP的程序就会给我一个答案。

所以总结一下求解的过程：

Hard-Margin的意思就是所有点都严格地被分开。如果没有这一条严格的线，就无解。

如果把线升高维度到一个hyperplane：

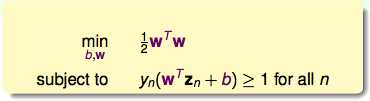
SVM可以看作是一种正则化的解释：

另一方面，SVM通过调整“胖瘦”的大小，其实可以间接地做VC Dimension的调节。

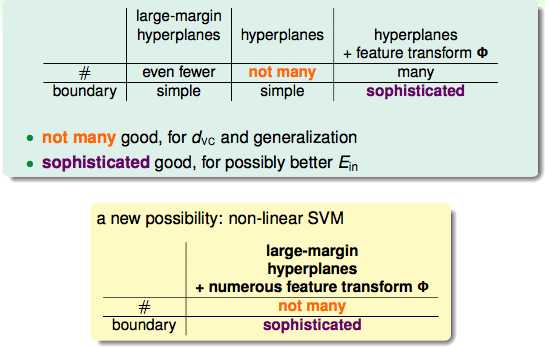
当我们通过Φ将线性不可分的数据升高维度到一个线性可分的维度的时候，我们用SVM就可以控制模型的复杂度。

总结：

机器学习技法(1)--Linear Support Vector Machine

标签：

原文地址：http://www.cnblogs.com/cyoutetsu/p/5917819.html