标签:
EM算法用于含有隐含变量的概率模型参数的极大似然估计。什么是隐含变量的概率模型呢?举个例子,假设有3枚硬币,分别记为A,B,C,它们正面出现的概率分别为r,p,q。每次实验先掷硬币A,如果出现的是正面就投B,如果出现的反面就投C,出现正面记为1,出现反面记为0。独立10次实验,观测结果如下:1101001011。如果只有这个结果,而不知道过程,问如何估计r,q,p?也就是说,我们能看到每次的观测结果,可是这个结果是B产生的还是C产生的我们不知道,也就是A的结果我们不知道,这个就是所谓的隐含变量。如果把观测变量用Y来表示,隐含变量(A的结果)用Z表示,那么观测数据的似然函数为:
\(P(Y|\theta)=\prod_i{rp^{y_i}(1-p)^{1-y_i}+(1-r)q^{y_i}(1-q)^{1-y_i}}\)
把上面的模型泛化一下可以概括为,有观测数据{\(x_1,x_2,...x_m\)},由一个具有观测变量X和隐含变量Z的模型产生,模型参数为\(\theta\),我们要最大化下面这个似然:
\(l(\theta)=\displaystyle\sum_{i}^{m}logp(x_i;\theta)=\displaystyle\sum_{i}^{m}log\sum_{z_i}p(x_i,z_i;\theta)\)。
直接求解这个优化问题非常困难。EM算法是通过迭代的方式求解,分为Expectation步和Maximization步。它的主要思想先找到目标函数的下边界,然后逐步提高这个下边界,进而得到一个最优解,但是这个最优解不一定是全局最优的。
下面看一下这个下界是怎么推导出来的---
\(\displaystyle\sum_{i}^{m}logp(x_i;\theta)\)
\(=\displaystyle\sum_{i}^{m}log\sum_{z_i}p(x_i,z_i;\theta)\)
对于i,假设\(Q_i\)是Z上的某个概率分布
\(=\displaystyle\sum_{i}^{m}log\sum_{z_i}Q_i(z_i)\frac{p(x_i,z_i;\theta)}{Q_i(z_i)}\)
\(>=\displaystyle\sum_{i}^{m}\sum_{z_i}Q_i(z_i)log\frac{p(x_i,z_i;\theta)}{Q_i(z_i)}\) ---- (eq1)
这一步用到了Jensen不等式,因为log函数是concave的(二阶导数小于0),所以有log(E(X))>=E(log(x))。而\(Q_i\)是概率分布,所以可以把\(\sum_{z_i}Q_i(z_i)\frac{p(x_i,z_i;\theta)}{Q_i(z_i)}\)看做是期望,然后可以套用Jensen不等式[2],即可得到上述结果。
现在有了下限,但是里面的Qi还不知道。怎么确定Qi呢?如果我们已经有了\(\theta\)的一个猜测值,那么这里自然让下限在\(\theta\)处值和似然函数在\(\theta\)处的值越接近越好,让不等式eq1在\(\theta\)处取得等号。因为log函数是严格凹函数,所以只有在E(X)==X(恒等于)的时候等号才会成立,比如当X是个常数的时候。基于上面的性质,令
\(\frac{p(x_i,z_i;\theta)}{Q_i(z_i)}=c\)
基于此,可以推出
\(\frac{\sum_zp(x_i,z;\theta)}{\sum_zQ_i(z)}=c\) (这个很容易推出来,a1/b1=c,a2/b2=c,a3/b3=c => (a2+a2+a3)/(b1+b2+b3)=c)
有,
\(Q_i(z_i)=\frac{p(x_i,z_i;\theta)}{\sum_zp(x_i,z;\theta)}\)
\(=\frac{p(x_i,z_i;\theta)}{p(x_i;\theta)}\)
\(=p(z_i|x_i;\theta)\)
因此,Qi是给定xi和\(\theta\)下zi的后验概率。
这就是E步骤,总结一下,假设已知\(\theta\),先求出似然函数的下限,然后求出隐含变量的分布Qi。
在接下来的M步骤,因为E步骤已经得到了一个Qi,这个步骤求最大化eq1的\(\theta\)值,也就是求下限的最大值点。
然后把M步骤求得的\(\theta\)输入E步骤,循环往复,直至收敛。
Repeat until convergence{
E-step:for each i,set
\(Q_i(z_i):=p(z_i|x_i;\theta)\)
M-step:set
\(\theta:=argmax_{\theta}\displaystyle\sum_{i}^{m}\sum_{z_i}Q_i(z_i)log\frac{p(x_i,z_i|\theta)}{Q_i(z_i)}\)
}
下面图片更直观的描述了EM过程,图片来自[4],E步挪动下界到\(\theta\)值与目标函数相同,M步求下界函数的最大值点做为新的\(\theta\)
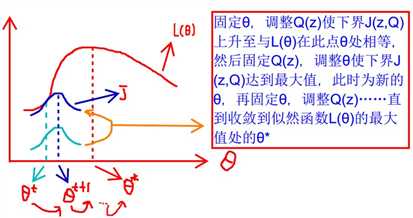
如果定义\(J(Q,\theta)=\displaystyle\sum_{i}^{m}\sum_{z_i}Q_i(z_i)log\frac{p(x_i,z_i;\theta)}{Q_i(z_i)}\)
那么,EM算法可以看做函数J的坐标轴下降过程,E步最大化Q,M步最大化\(\theta\)。
EM算法是会收敛的,具体的证明参见参考[3],但是EM算法有可能陷入局部最优的,它对初始值敏感。
下面尝试用EM算法解决文章开始的三硬币问题。
假设已经经过了j步的迭代,现在已经有了\(\theta^j=(r^j,c^j,q^j)\) (为了避免写起来混淆,把参数里面B的正面概率p变成了c)
E步:
这里要求\(p(z_i|x_i;\theta^j)\),因为是二分问题,为了描述简便,可以直接求正面的概率,根据贝叶斯概率公式:
(为了书写简单,下面把表示迭代次数的上角标j去掉了,心里记得,r,c,q是已知的)
\(p(z_i=1|x_i;\theta)=\frac{p(x_i|z_i=1;\theta)p(z_i=1;\theta)}{p(x_i|z_i=1;\theta)p(z_i=1;\theta)+p(z_i=0;\theta)p(x_i|z_i=0;\theta)}\)
\(=\frac{rc^{x_i}(1-c)^{(1-x_i)}}{rc^{x_i}(1-c)^{1-x_i}+(1-r)q^{x_i}(1-q)^{(1-x_i)}}\)
把\(p(z_i=1|x_i;\theta)\)记做\(\mu^{(j+1)}\)表示是第j+1次迭代得到的值,为了书写清楚一下(cnblog对公式支持的有些差啊),还是把上角标去掉了
M步骤:
现在\(p(z_i|x_i;\theta)\)已经知道,就开始解决下面这个优化问题了
\(J(\theta)=\sum\mu_ilog\frac{p(x_i,z_i=1;\theta)}{\mu_i}+(1-\mu_i)log\frac{p(x_i,z_i=0;\theta)}{1-\mu_i}\)
\(=\sum\mu_ilog\frac{rc^{x_i}(1-c)^{(1-x_i)}}{\mu_i}+(1-\mu_i)log\frac{(1-r)q^{x_i}(1-q)^{(1-x_i)}}{1-\mu_i}\)
令\(\frac{\partial J(\theta)}{r}=0\)
很容易可以得到\(r=\frac{1}{m}\sum\mu_i\)
令\(\frac{\partial J(\theta)}{c}=0\)
同样容易得到\(c=\frac{\sum\mu_ix_i}{\sum\mu_i}\)
令\(\frac{\partial J(\theta)}{q}=0\)
同样容易得到\(c=\frac{\sum(1-\mu_i)x_i}{\sum(1-\mu_i)}\) 参考[1][5]
参考:
[1]李航《统计学习方法》
[2]Jensen不等式:http://www.cnblogs.com/naniJser/p/5642288.html
[3]Andrew Ng机器学习课程的讲义:http://cs229.stanford.edu/notes/cs229-notes8.pdf
[4]介绍EM算法的blog:http://blog.csdn.net/zouxy09/article/details/8537620
[5]http://chenrudan.github.io/blog/2015/12/02/emexample.html
标签:
原文地址:http://www.cnblogs.com/naniJser/p/5894423.html