标签:
Floyd算法:
Floyd算法用来找出每对顶点之间的最短距离,它对图的要求是,既可以是无向图也可以是有向图,边权可以为负,但是不能存在负环.
基本算法:
Floyd算法基于动态规划的思想,以 u 到 v 的最短路径至少经过前 k 个点为转移状态进行计算,通过 k 的增加达到寻找最短路径的目的.当 k 增加 1 时,最短路径要么不边,如果改变,必经过第 k 各点,也就是说当起点 u 到第 k 个点的最短距离加上第 k 个点到终点 v 的最短路径小于不经过第 k 个节点的最优最短路经长度的时候更新 u 到 v 的最短距离. 当 k = n 时, u 到 v 的最短路径就确定了.
伪代码:
图的存储用邻接矩阵 gra[][] 来记录,如果 u 与 v 之间没有边直接相连,则 gra[u][v] = INF; dist[][] 记录最终的最短路. pre[i][j] 存储 i 到 j 路径中 i 的后一个节点.
1): 初始化:将 gra 中的数据复制到 dist 中作为每对顶点间的最短路的除值, pre[i][j] = j;
2): k 从 1 到 n 循环 n 次, 每次循环中枚举图中不同的两点 u, v, 如果 dist[u][v] > dist[u][k] + dist[k][v], 则更新 dist[u][v] = dist[u][k] + dist[k][v], 更新 pre[u][v] = pre[u][k].
3): 最后 dist[u][v] 数组中存储的就是 u 到 v 的最短距离, u 到 v 的路径, 则可以按照顺序查找就好了.
以图为例:
有一个如下的无向图, “D” 表表示最短路表, “P” 表表示最短路径表:
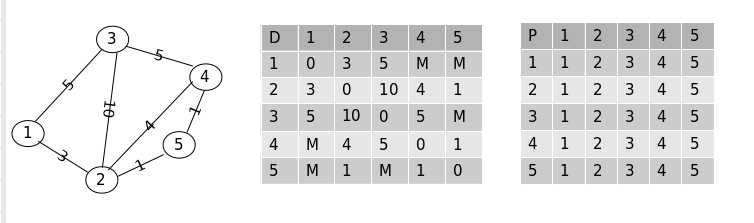
假设现在每对顶点之间的路径只允许经过点 “1” , 则更新后的每对顶点之间的距离:
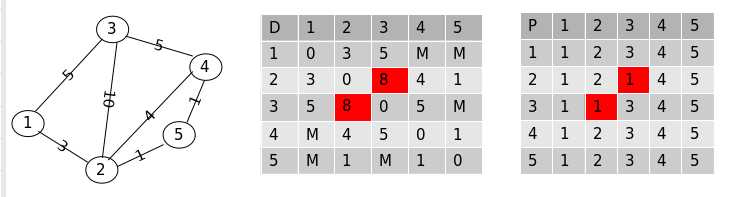
这里看到点 “2” 到点 “3” 的距离经过点 “1” 得到了更新,同时更新了用于记录路径的 P 数组.
第二步,允许每对顶点之间的最短路径经过点 “1” 和点 “2”,则更新后的数组为:
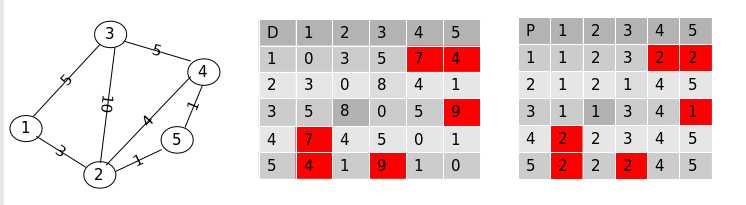
可以看到得到更新的路径为:
1 ---> 4, 经过点 “2” 得到更新
1 ---> 5, 经过点 “2” 得到更新
3 ---> 5. 经过点 “1 --- > 2” 得到更新
第三步: 允许经过点 “1”, “2” 和点 “3” 则更新后的数组为:
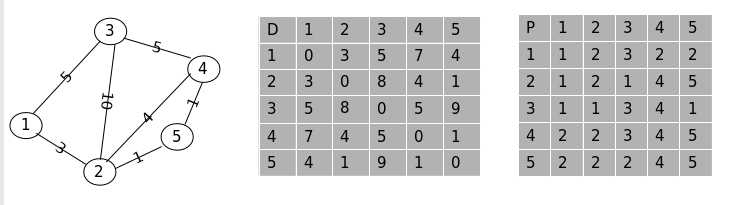
这则说明,上一步的最短路径不需要更新.
第四步, 允许经过点 “1”, “2” , “3” 和点 “4” 则更新后的数组为:
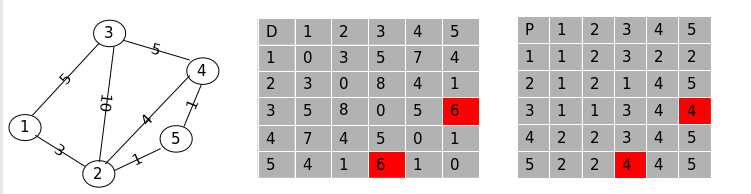
可以看到 3 ---> 5 的路径经过点 “4” 得到了更新(原先是 3 ---> 1 ---> 2 ---> 5, w = 9)
第五步, 允许任意两点之间的最短路径可以经过全部点,则更新后的数组为:
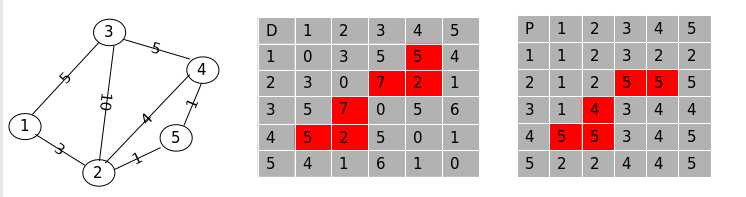
这次得到更新的路径为:
1 ---> 4 的路径. 更新为 “1 ---> 2 ---> 5 ---> 4, w = 5” (原路径为 1 ---> 2 ---> 4, w = 7)
2 ---> 3 的路径. 更新为 “2 ---> 5 ---> 4 ---> 3, w = 7” (原路经为 2 ---> 1 ---> 3, w = 8)
2 ---> 4 的路径. 更新为 “2 --> 5 --> 4, w = 2” (原路径为 2 ---> 4, w = 4)
无向图反之亦然.
至此最短路径就寻找完毕. dist[i][j] 数组里面保存的就是 i 到 j 的最短距离.如果要查寻路径, 则按照查数组 pre 就好.比如查询 “2” 到 “3” 的路径:
则寻找 pre[2][3] = 5, 2 ---> 5
继续寻找 pre[5][3] = 4, 2 ---> 5 ---> 4
继续寻找 pre[4][3] = 3, 2 ---> 5 ---> 4 ---> 3
由于此时 i = j = 3, 则 “2” 到 “3” 的最短路径已找到为: 2 ---> 5 ---> 4 ---> 3
代码( 时间复杂度O(N3) ):
1 #include <bits/stdc++.h> 2 3 typedef long long LL; 4 const int MAXN = 100; 5 const int INF = 0x3f3f3f3f; 6 using namespace std; 7 8 int pre[MAXN + 3][MAXN + 3], dist[MAXN + 3][MAXN + 3]; //pre 储存路径 dist最短距离 9 void floyd(int n, int gra[][MAXN + 3]) { 10 for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) dist[i][j] = gra[i][j], pre[i][j] = j; //初始化 11 for(int k = 1; k <= n; k++) { //尝试经过 k 个点对每对顶点之间的距离进行更新 12 for(int i = 1; i <= n; i++) { 13 for(int j = 1; j <= n; j++) { 14 if(dist[i][k] != INF && dist[k][j] != INF && dist[i][k] + dist[k][j] < dist[i][j]) { 15 dist[i][j] = dist[i][k] + dist[k][j]; 16 pre[i][j] = pre[i][k]; 17 } 18 } 19 } 20 } 21 } 22 23 int pfpath(int u, int v) { //打印最短路径 24 while(u != v) { 25 cout << u << " "; 26 u = pre[u][v]; 27 } 28 cout << u << endl; 29 } 30 31 int gra[MAXN + 3][MAXN + 3]; 32 int main() { 33 int n, m; 34 while(cin >> n >> m){ // n 个点, m 条边 35 for(int i = 0; i <= n; i++) for(int j = -1; j <= n; j++){ 36 gra[i][j] = (i == j ? 0 : INF); 37 } 38 for(int i = 0; i < m; i++) { 39 int u, v, w; cin >> u >> v >> w; 40 gra[u][v] = gra[v][u] = w; //无向图 41 } 42 floyd(n, gra); 43 } 44 return 0; 45 }
参考资料《图论及应用》
标签:
原文地址:http://www.cnblogs.com/Ash-ly/p/5920953.html