标签:
【例2-5】整数划分问题
在正整数n的所有不同划分中,最大加数n1不大于m的划分个数记做q(n,m)。可以建立q(n,m)的如下递归关系。
(1)q(n,1)=1,n≥1
当最大加数n1不大于1时,任何正整数n只有一种划分形式,即n=1+1+…+1.(n个1)
(2)q(n,m)=q(n,n),m≥n
最大加数n1实际上不大于n。因此q(1,m)=1.
(3)q(n,n)=1+q(n,n-1)
正整数n的划分由n1=n的划分和n1≤n-1的划分组成。
(4)q(n,m)=q(n,m-1)+q(n-m,m),n>m>1
正整数n的最大加数n1不大于m的划分由n1=m的划分和n1≤m-1的划分组成。
证明:(a)划分中包含m的情况,即{m,{x1,x2,...,xi}},其中{x1,x2,...,xi}的和为n-m,可能再次出现m,所有划分个数为q(n-m,m).
(b)划分中不包含m的情况,则划分中所有的值都比m小,即n的(m-1)划分,个数为q(n,m-1);
所以q(n,m)=q(n-m,m)+q(n,m-1);
以上的关系实际上给出了计算q(n,m)的递归式如下:
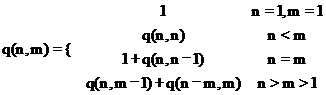
Int q(int n,int m)
{
If((n=1)||(m<1)) return 0;
If((n==1)||(m==1)) return 1;
If(n<m) return q(n,n);
If(n==m) return 1+q(n,n-1);
Return q(n,m-1)+q(n-m,m);
}
标签:
原文地址:http://www.cnblogs.com/vincyLu/p/5928067.html