标签:
第三章 算法
前言:许多人对算法的看法是截然不同的,我之前提到过了。不过,我要说的还是那句话:算法体现编程思想,编程思想指引算法。
同时,有许多人认为简单算法都太简单了,应当去学习一些更为实用的复杂算法。不过,许多复杂算法都是从简单算法演绎而来的,这里就不一一举例了。而且,算法千千万万。更为重要的是从算法中体会编程的思想。
4.1 简单问题算法
PS:接下来是一些入门问题,简单到都没有具体算法可言。但这些问题是我们当初对算法的入门。如果不喜欢,可以跳过。
实例111 任意次方后的最后三位
问题:编程实现一个整数任意次方后的最后三位数,即求xy的最后三位数,x和y的值由键盘输入。
逻辑:无论是刚接触编程还是现在,看到这个问题,你的脑海里都不会出现一个有名有姓的具体算法。但是,你却能够找到解决问题的逻辑步骤。而这个逻辑步骤的清晰指令就是算法。其次,这种情况不仅仅面对这题。当以后遇到诸多问题时都是这样,了解问题->分析问题->建立模型->寻找算法->编写程序->解决问题。最后,这题还体现了我在之前篇章强调的一点,编程解决问题的同时,还可以依靠数学的思想简化问题及程序。这题如果直接计算xy,也许还没等我们提取xy最后三位,xy的值就越界了。所以在每一次循环计算z*x之后,取z*x的最后三位作为z的值。其实,如果x的值大于999,也可以取x的后三位为新的x,结果不变。
代码:
1 #include<stdio.h>
2 main()
3 {
4 int i, x, y, z = 1;
5 printf("please input two numbers x and y(x^y):\n");
6 scanf("%d%d", &x, &y);
7 //输入底数和幂数
8 for (i = 1; i <= y; i++)
9 z = z * x % 1000;
10 //计算一个数任意次方的后三位
11 printf("the last 3 digits of %d^%d is:%d\n", x, y, z);
12 //输出最终结果
13 }
反思&总结:一个简单的问题,往往也可以从中分析到许多重要结论。就如同接下来许多算法,虽然简单、基础,却也是日后复杂算法的基础。
4.2 排序算法
PS:排序是数据处理中的一种重要算法。其中由于待排序的记录数量不同,使得排序过程中涉及的存储器不同,可将排序算法分为两大类:内部排序(待排序记录存放在RAM)与外部排序(排序过程中涉及ROM)。排序算法众多,最好的算法往往是与需求相关的。不过从使用上来说,频率最高的是归并排序,快速排序,堆排序(因为当n较大时,时间复杂度O(nlog2n)的上述三种算法最为迅捷)。
PS:从网络上找到的一张图。
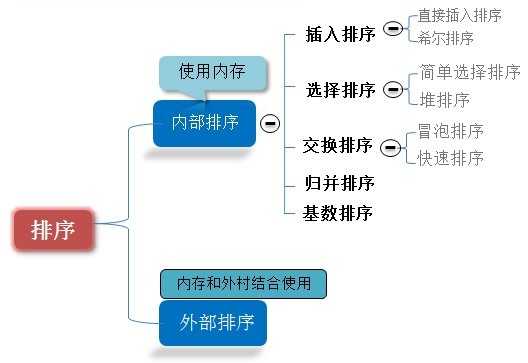
实例119 直接插入排序
问题:通过直接插入排序,编程实现排序。
逻辑:插入排序是将一个数据插入到已排序的有序序列中,使得整个序列在插入了该数据后仍然有序(默认单个数据的序列为有序序列)。插入排序中较为简单的一种方法便是直接插入排序,它插入的位置的确定是通过将待插入的数据与有序区中的个数据自左向右依次比较其关键字值大小来确定的。
代码:
1 #include <stdio.h> 2 void insort(int s[], int n) 3 /*自定义函数isort*/ 4 { 5 int i, j; 6 for (i = 2; i <= n; i++) 7 /*数组下标从2开始,0做监视哨,1一个数据无可比性*/ 8 { 9 s[0] = s[i]; 10 /*给监视哨赋值*/ 11 j = i - 1; 12 /*确定要进行比较的元素的最右边位置*/ 13 while (s[0] < s[j]) 14 { 15 s[j + 1] = s[j]; 16 /*数据右移*/ 17 j--; 18 /*移向左边一个未比较的数*/ 19 } 20 s[j + 1] = s[0]; 21 /*在确定的位置插入s[i]*/ 22 } 23 } 24 main() 25 { 26 int a[11], i; 27 /*定义数组及变量为基本整型*/ 28 printf("please input number:\n"); 29 for (i = 1; i <= 10; i++) 30 scanf("%d", &a[i]); 31 /*接收从键盘中输入的10个数据到数组a中*/ 32 printf("the original order:\n"); 33 for (i = 1; i < 11; i++) 34 printf("%5d", a[i]); 35 /*将为排序前的顺序输出*/ 36 insort(a, 10); 37 /*调用自定义函数isort()*/ 38 printf("\nthe sorted numbers:\n"); 39 for (i = 1; i < 11; i++) 40 printf("%5d", a[i]); 41 /*将排序后的数组输出*/ 42 printf("\n"); 43 }
PS:设立监视哨是为了避免数据在后移时丢失。
反思:直接插入算法应该是大多数人接触的第一个算法了。但是,有多少人自己将这个算法进一步优化呢?
实例120 希尔排序
问题:通过希尔排序,编程实现排序。
逻辑:希尔排序是在直接插入排序的基础上进行了改进。将要排序的序列按固定增量d分成若干组,即将等距离者(相距d的数据)划分在同一组中,再在组内进行直接插入排序。然后减小增量d,再在新划分的组内进行直接插入排序。重复上述操作,直至增量d减小到1(即所有数据都放在了同一组内进行直接插入排序)。

代码:
1 #include <stdio.h>
2 void shsort(int s[], int n)
3 /*自定义函数shsort*/
4 {
5 int i, j, d;
6 d = n / 2;
7 /*确定固定增量值*/
8 while (d >= 1)
9 {
10 for (i = d + 1; i <= n; i++)
11 /*数组下标从d+1开始进行直接插入排序*/
12 {
13 s[0] = s[i];
14 /*设置监视哨*/
15 j = i - d;
16 /*确定要进行比较的元素的最右边位置*/
17 while ((j > 0) && (s[0] < s[j]))
18 {
19 s[j + d] = s[j];
20 /*数据右移*/
21 j = j - d;
22 /*向左移d个位置*/
23 }
24 s[j + d] = s[0];
25 /*在确定的位置插入s[i]*/
26 }
27 d = d / 2;
28 /*增量变为原来的一半*/
29 }
30 }
31 main()
32 {
33 int a[11], i;
34 /*定义数组及变量为基本整型*/
35 printf("please input numbers:\n");
36 for (i = 1; i <= 10; i++)
37 scanf("%d", &a[i]);
38 /*从键盘中输入10个数据*/
39 shsort(a, 10);
40 /*调用shsort()函数*/
41 printf("the sorted numbers:\n");
42 for (i = 1; i <= 10; i++)
43 printf("%5d", a[i]);
44 /*将排好序的数组输出*/
45 }
反思:其实希尔排序就是一个分组排序。通过比较固定距离(称为增量)的数据,使得在数据的一次移动时可能跨过多个元素,则在一次数据比较就可能消除多个数据交换。而这就是希尔排序较直接插入排序的美丽之处。
实例120.5.1 简单选择排序
问题:通过简单选择排序,编程实现排序。
逻辑:从待排序区间中找出关键字值最小(/最大)的数据(选择),将其与待排序区间第一个数据a[0]交换(默认本身可以与本身交换).将其中再从剩余的待排序区间(a[1]-a[n])重复上述操作,直至最后一个数据完成交换。
代码:
1 #include <stdio.h>
2 main()
3 {
4 int i, j, t, a[11];
5 /*定义变量及数组为基本整型*/
6 printf("please input 10 numbers:\n");
7 for (i = 1; i < 11; i++)
8 scanf("%d", &a[i]);
9 /*从键盘中输入要排序的10个数字*/
10 for (i = 1; i <= 9; i++)
11 for (j = i + 1; j <= 10; j++)
12 if (a[i] > a[j])
13 /*如果后一个数比前一个数大则利用中间变量t实现俩值互换*/
14 {
15 t = a[i];
16 a[i] = a[j];
17 a[j] = t;
18 }
19 printf("the sorted numbers:\n");
20 for (i = 1; i <= 10; i++)
21 printf("%5d", a[i]);
22 /*将排好序的数组输出*/
23 }
反思:简单选择排序存在其改进算法——二元选择排序,简单选择排序每次循环都只能确定一个数据(关键字值最大/最小)的定位。那么在每次循环同时确定关键字值最大和关键字值最小的数据,那么就可以在n/2次循环后完成排序。
实例120.5.2 堆排序
问题:通过堆排序,编程实现排序。
逻辑:堆排序是一种树形选择排序,是对直接选择算法更为彻底的改进。堆排序中的堆指代的就是完全二叉树。堆又分为:大根堆和小根堆。大根堆要求完全二叉树中的每个节点的值都不大于其父节点的值。根据定义,大根堆的堆顶一定是关键字值最大的。同理,可理解小堆根的定义与堆顶关键字值最小。
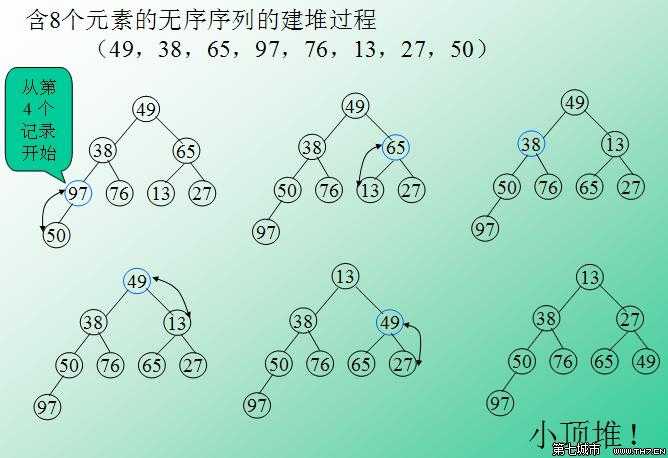
(图片选自网络资源)
代码:(经过考虑,还是选了兰亭风雨的代码,比较易于理解)
1 #include<stdio.h>
2 #include<stdlib.h>
3 /* arr[start+1...end]满足最大堆的定义, 将arr[start]加入到最大堆arr[start+1...end]中, 调整arr[start]的位置,使arr[start...end]也成为最大堆 注:由于数组从0开始计算序号
4
5 ,也就是二叉堆的根节点序号为0, 因此序号为i的左右子节点的序号分别为2i+1和2i+2 */
6 void HeapAdjustDown(int *arr,int start,int end)
7 {
8 int temp=arr[start];
9 //保存当前节点
10 int i=2*start+1;
11 //该节点的左孩子在数组中的位置序号
12 while(i<=end)
13 {
14 //找出左右孩子中最大的那个
15 if(i+1<=end && arr[i+1]>arr[i])
16 i++;
17 //如果符合堆的定义,则不用调整位置
18 if(arr[i]<=temp)
19 break;
20 //最大的子节点向上移动,替换掉其父节点
21 arr[start]=arr[i];
22 start=i;
23 i=2*start+1;
24 }
25 arr[start]=temp;
26 }
27 /* 堆排序后的顺序为从小到大 因此需要建立最大堆 */
28 void Heap_Sort(int *arr,int len)
29 {
30 int i;
31 //把数组建成为最大堆
32 //第一个非叶子节点的位置序号为(len-1)/2 for(i=(len-1)/2;i>=0;i--)
33 for(i=(len-1)/2;i>=0;i--)
34 HeapAdjustDown(arr,i,len-1);
35 //进行堆排序 for(i=len-1;i>0;i--)
36 for(i=len-1;i>0;i--)
37 {
38 //堆顶元素和最后一个元素交换位置,
39 //这样最后的一个位置保存的是最大的数,
40 //每次循环依次将次大的数值在放进其前面一个位置,
41 //这样得到的顺序就是从小到大
42 int temp=arr[i];
43 arr[i]=arr[0];
44 arr[0]=temp;
45 //将arr[0...i-1]重新调整为最大堆
46 HeapAdjustDown(arr,0,i-1);
47 }
48 }
49 int main()
50 {
51 int num;
52 printf("请输入排序的元素的个数:");
53 scanf("%d",&num);
54 int i;
55 int *arr = (int *)malloc(num*sizeof(int));
56 printf("请依次输入这%d个元素(必须为整数):",num);
57 for(i=0;i<num;i++)
58 scanf("%d",arr+i);
59 printf("堆排序后的顺序:");
60 Heap_Sort(arr,num);
61 for(i=0;i<num;i++)
62 printf("%d ",arr[i]);
63 printf("\n");
64 free(arr);
65 arr = 0;
66 return 0;
67 }
反思:由于开始建立初始堆时比较次数较多,故不适合数据较少的排序。
实例121 冒泡排序
问题:通过冒泡排序,编程实现排序。
逻辑:冒泡排序可以说是直接排序后遇到的最早的排序方法,同时也是许多C语言入门考试的重点。对n个数据进行冒泡排序,那么就要进行n-1趟比较(PS:在第j趟比较中要进行n-j次两两比较)。每次通过比较相邻的两个数据,将关键字值较小的上升(下降),将关键字值较大的下降(上升)。由于这样的模式就像是水中的泡泡在上升,故命名为冒泡排序。
代码:
1 #include <stdio.h> 2 main() 3 { 4 int i, j, t, a[11]; 5 /*定义变量及数组为基本整型*/ 6 printf("please input 10 numbers:\n"); 7 for (i = 1; i < 11; i++) 8 scanf("%d", &a[i]); 9 /*从键盘中输入10个数*/ 10 for (i = 1; i < 10; i++) 11 /*变量i代表比较的趟数*/ 12 for (j = 1; j < 11-i; j++) 13 /*变量j代表每趟两两比较的次数*/ 14 if (a[j] > a[j + 1]) 15 { 16 t = a[j]; 17 /*利用中间变量实现俩值互换*/ 18 a[j] = a[j + 1]; 19 a[j + 1] = t; 20 } 21 printf("the sorted numbers:\n"); 22 for (i = 1; i <= 10; i++) 23 printf("%5d", a[i]); 24 /*将冒泡排序后的顺序输出*/ 25 }
反思:冒泡排序算法是一个看到名字就可以想象到其原理的一个算法。所以是很好理解、记忆的。
实例122 快速排序
问题:通过快速排序,编程实现排序
逻辑:快速排序是冒泡排序的一种改进。主要的算法思想是在待排序的n个数据中去第一个数据作为基准值,将所有的数据分为3组,使得第一组中各数据均小于或等于基准值,第二组便是做基准值的数据,第三组中个数据均大于或等于基准值。这就实现了第一趟分割,然后对第一组和第三组分别重复上述方法,以此类推,直到每组中只有一个数据为止。
代码:
1 #include <stdio.h>
2 void qusort(int s[], int start, int end)
3 /*自定义函数qusort()*/
4 {
5 int i, j;
6 /*定义变量为基本整型*/
7 i = start;
8 /*将每组首个元素赋给i*/
9 j = end;
10 /*将每组末尾元素赋给j*/
11 s[0] = s[start];
12 /*设置基准值*/
13 while (i < j)
14 {
15 while (i < j && s[0] < s[j])
16 j--;
17 /*位置左移*/
18 if (i < j)
19 {
20 s[i] = s[j];
21 /*将s[j]放到s[i]的位置上*/
22 i++;
23 /*位置右移*/
24 }
25 while (i < j && s[i] <= s[0])
26 i++;
27 /*位置右移*/
28 if (i < j)
29 {
30 s[j] = s[i];
31 /*将大于基准值的s[j]放到s[i]位置*/
32 j--;
33 /*位置右移*/
34 }
35 }
36 s[i] = s[0];
37 /*将基准值放入指定位置*/
38 if (start < i)
39 qusort(s, start, j - 1);
40 /*对分割出的部分递归调用函数qusort()*/
41 if (i < end)
42 qusort(s, j + 1, end);
43 }
44 main()
45 {
46 int a[11], i;
47 /*定义数组及变量为基本整型*/
48 printf("please input numbers:\n");
49 for (i = 1; i <= 10; i++)
50 scanf("%d", &a[i]);
51 /*从键盘中输入10个要进行排序的数*/
52 qusort(a, 1, 10);
53 /*调用qusort()函数进行排序*/
54 printf("the sorted numbers:\n");
55 for (i = 1; i <= 10; i++)
56 printf("%5d", a[i]);
57 /*输出排好序的数组*/
58 }
反思:快速排序与希尔排序都采用了分组排序来优化已有的排序方法。其实对算法及其他许多方面而言,多线操作有着许多优势。只是这可能在一定程度上,人们大脑不习惯,从而导致人们忽视计算机在这方面的优势。就好像许多人在研究人工智能,我并不赞同一味地追求让计算机和人类大脑一样思考,工作。宇宙中的每一件东西都有着其独特的魅力,人类只是宇宙的一员,并没有超脱其上。那么为什么一切都以人类的视角去考虑问题呢?
实例124 归并排序
问题:通过归并排序,编程实现排序。
逻辑:归并是将两个或者多个有序记录序列合并成一个有序序列。归并方法有多种,一次对两个有序记录序列进行归并,成为两路归并排序,也有三路归并排序及多路归并排序。不过,这次代码采用的是两路归并排序。其实学会两路,多路也就会了。
代码:
1 #include <stdio.h>
2 void merge(int r[], int s[], int x1, int x2, int x3)
3 /*实现一次归并排序函数*/
4 {
5 int i, j, k;
6 i = x1;
7 /*第一部分的开始位置*/
8 j = x2 + 1;
9 /*第二部分的开始位置*/
10 k = x1;
11 while ((i <= x2) && (j <= x3))
12 /*当i和j都在两个要合并的部分中*/
13 if (r[i] <= r[j])
14 /*筛选两部分中较小的元素放到数组s中*/
15 {
16 s[k] = r[i];
17 i++;
18 k++;
19 }
20 else
21 {
22 s[k] = r[j];
23 j++;
24 k++;
25 }
26 while (i <= x2)
27 /*将x1~x2范围内的未比较的数顺次加到数组r中*/
28 s[k++] = r[i++];
29 while (j <= x3)
30 /*将x2+1~x3范围内的未比较的数顺次加到数组r中*/
31 s[k++] = r[j++];
32 }
33 void merge_sort(int r[], int s[], int m, int n)
34 {
35 int p;
36 int t[20];
37 if (m == n)
38 s[m] = r[m];
39 else
40 {
41 p = (m + n) / 2;
42 merge_sort(r, t, m, p);
43 /*递归调用merge_sort函数将r[m]~r[p]归并成有序的t[m]~t[p]*/
44 merge_sort(r, t, p + 1, n);
45 /*递归调用merge_sort函数将r[p+1]~r[n]归并成有序的t[p+1]~t[n]*/
46 merge(t, s, m, p, n);
47 /*调用函数将前两部分归并到s[m]~s[n]*/
48 }
49 }
50 main()
51 {
52 int a[11];
53 int i;
54 printf("please input 10 numbers:\n");
55 for (i = 1; i <= 10; i++)
56 scanf("%d", &a[i]);
57 /*从键盘中输入10个数*/
58 merge_sort(a, a, 1, 10);
59 /*调用merge_sort函数进行归并排序*/
60 printf("the sorted numbers:\n");
61 for (i = 1; i <= 10; i++)
62 printf("%5d", a[i]);
63 /*将排序后的结构输出*/
64 }
反思:其实,就我感觉,归并排序并不是指一种排序方法。而是对多个排序方法的一种综合体现。
实例124.50 基数排序
问题:通过基数排序,编程实现排序。
逻辑:基数排序属于分配式排序,是透过关键字值的各位键值咨询来排序。这种排序方法说实话解释麻烦,但通过例子一眼就懂。
例子:
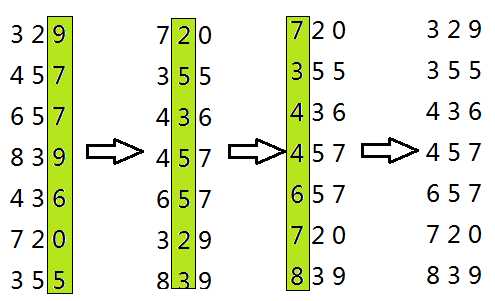
(图片选自网络资源)
代码:(此处略过,主要这种排序难点只在于理解。有了上面的例子图片,就十分简单了。提取各数位值的方法之前就学过了。)
反思:说实话,当我第一次看到这个算法时,我第一反应是编码。这个算法最精彩的地方是它从另外一个角度向大家展示了排序的方法。这个算法可以说另辟蹊径。
总结:排序算法只介绍这些常用的八种基础算法。虽然没有囊括所有的算法,但这八种算法也展现了大部分排序算法的思路。可以多多体会。
4.3 查找算法
PS:查找算法时数据处理中使用较为频繁的一种操作了。当数据量较大时,一个优秀的查找算法就可以带来惊人的效益了。
PS:常见查找算法分为四类:顺序查找、二分查找、分块查找、哈希(散列)查找。
实例125 顺序查找
问题:通过顺序查找,编程完成数据查找
逻辑:由于顺序查找最为符合多数人查找的逻辑,所以较为简单,故顺序查找一般是大家最早接触的查找算法。说白了,就是开着循环,遍历所有数据,比对着每一个遍历到的数据,直到找到需要的数据。
代码:
1 #include <stdio.h>
2 void search(int key, int a[], int n)
3 /*自定义函数search*/
4 {
5 int i, count = 0, count1 = 0;
6 for (i = 0; i < n; i++)
7 {
8 count++;
9 /*count记录查找次数*/
10 if (a[i] == key)
11 /*判断要查找的关键字与数组中的元素是否相等*/
12 {
13 printf("search %d times a[%d]=%d\n", count, i, key);
14 /*输出查找次数及在数组中的位置*/
15 count1++;
16 /*count1记录查找成功次数*/
17 }
18 }
19 if (count1 == 0)
20 /*判断是否查找到h*/
21 printf("no found!");
22 /*如果未查找到输出no found*/
23 }
24 main()
25 {
26 int n, key, a[100], i;
27 printf("please input the length of array:\n");
28 scanf("%d", &n);
29 /*输入要输入的元素个数*/
30 printf("please input element:\n");
31 for (i = 0; i < n; i++)
32 scanf("%d", &a[i]);
33 /*输入元素存到数组a中*/
34 printf("please input the number which do you want to search:\n");
35 scanf("%d", &key);
36 /*指定要查找的元素*/
37 search(key, a, n);
38 /*调用自定义的search函数*/
39 }
反思:由于顺序查找算法贴近人的逻辑,所以一般入门C的查找算法考试范围里只有顺序查找算法这一种。其实许多人,包括学过和没学过的,提到查找算法时,都第一个想到顺序查找算法。甚至只想到顺序查找算法。可惜,就如同暴力破解密码一般,顺序查找算法一般是所有查找算法内最为耗时的。所以,还是要记住其他查找算法的。
实例126 二分查找
问题:通过二分查找,编程实现数据查找。
逻辑:二分查找又称折半查找,针对且只针对于有序表。首先选取有序表中间位置的数据,将其关键字于给定的关键字key进行比较,若相等,则查找成功;若key的值较大,则要找的数据一定在右子表中,继续对右子表进行二分查找;若key的值较小,则要找的数据一定在左子表中,继续对左子表进行二分查找。如此类推,直到查找成功或者查找失败。
代码:
1 #include <stdio.h>
2 void binary_search(int key, int a[], int n)
3 /*自定义函数binary_search*/
4 {
5 int low, high, mid, count = 0, count1 = 0;
6 low = 0;
7 high = n - 1;
8 while (low < high)
9 /*当查找范围不为0时执行循环体语句*/
10 {
11 count++;
12 /*count记录查找次数*/
13 mid = (low + high) / 2;
14 /*求出中间位置*/
15 if (key < a[mid])
16 /*当key小于中间值*/
17 high = mid - 1;
18 /*确定左子表范围*/
19 else if (key > a[mid])
20 /*当key大于中间值*/
21 low = mid + 1;
22 /*确定右子表范围*/
23 else if (key == a[mid])
24 /*当key等于中间值证明查找成功*/
25 {
26 printf("success!\nsearch %d times!a[%d]=%d", count, mid, key);
27 /*输出查找次数及所查找元素在数组中的位置*/
28 count1++;
29 /*count1记录查找成功次数*/
30 break;
31 }
32 }
33 if (count1 == 0)
34 /*判断是否查找失败*/
35 printf("no found!");
36 /*查找失败输出no found*/
37 }
38 main()
39 {
40 int i, key, a[100], n;
41 printf("please input the length of array:\n");
42 scanf("%d", &n);
43 /*输入数组元素个数*/
44 printf("please input the element:\n");
45 for (i = 0; i < n; i++)
46 scanf("%d", &a[i]);
47 /*输入有序数列到数组a中*/
48 printf("please input the number which do you want to search:\n");
49 scanf("%d", &key);
50 /*输入要查找的关键字*/
51 binary_search(key, a, n);
52 /*调用自定义函数*/
53 }
反思:其实二分查找就好像高中数学中“二分法”一样。所以也较为容易理解。虽然这种算法极为快捷,可惜该种查找算法只针对有序表。所以仍然需要学习其他算法。
实例127 分块查找
问题:通过分块查找,编程实现数据查找
逻辑:分块查找,又称为索引顺序查找,是对顺序查找和折半查找的综合改进。其实从分块、索引二词就可以知道起思想。通过对数据的分块,不同块负责放下不同范围的数据,不可以存在重叠数据范围。当需要查找一个给定数据时,可以通过索引表来确定数据范围,从而确定到具体的一个数据块,借此来提升效率。
代码:
1 #include <stdio.h>
2 struct index
3 /*定义块的结构*/
4 {
5 int key;
6 int start;
7 int end;
8 } index_table[4];
9 /*定义结构体数组*/
10 int block_search(int key, int a[])
11 /*自定义实现分块查找*/
12 {
13 int i, j;
14 i = 1;
15 while (i <= 3 && key > index_table[i].key)
16 /*确定在那个块中*/
17 i++;
18 if (i > 3)
19 /*大于分得的块数,则返回0*/
20 return 0;
21 j = index_table[i].start;
22 /*j等于块范围的起始值*/
23 while (j <= index_table[i].end && a[j] != key)
24 /*在确定的块内进行查找*/
25 j++;
26 if (j > index_table[i].end)
27 /*如果大于块范围的结束值,则说明没有要查找的数,j置0*/
28 j = 0;
29 return j;
30 }
31 main()
32 {
33 int i, j = 0, k, key, a[16];
34 printf("please input the number:\n");
35 for (i = 1; i < 16; i++)
36 scanf("%d", &a[i]);
37 /*输入由小到大的15个数*/
38 for (i = 1; i <= 3; i++)
39 {
40 index_table[i].start = j + 1;
41 /*确定每个块范围的起始值*/
42 j = j + 1;
43 index_table[i].end = j + 4;
44 /*确定每个块范围的结束值*/
45 j = j + 4;
46 index_table[i].key = a[j];
47 /*确定每个块范围中元素的最大值*/
48 }
49 printf("please input the number which do you want to search:\n");
50 scanf("%d", &key);
51 /*输入要查询的数值*/
52 k = block_search(key, a);
53 /*调用函数进行查找*/
54 if (k != 0)
55 printf("success.the position is :%d\n", k);
56 /*如果找到该数,则输出其位置*/
57 else
58 printf("no found!");
59 /*若未找到则输出提示信息*/
60 }
反思:分块查找算法是通过将顺序查找和二分查找综合而来。效率处于两者之间,同样缺点也是有的。虽然分块查找算法不需要数据表呈线性,但需要建立有序索引表。所有,相对而言,分块查找更加适应于需要多次查找的数据表。
实例128 哈希查找
问题:通过哈希查找,编程实现数据查找。
逻辑: 哈希查找可以说是这四类查找方法中最为复杂的查找方法。主要它的处理方法并不唯一,相反还很多。
哈希查找是通过给定哈希函数计算数据存储位置的方法。操作步骤:1)利用给定的哈希函数计算,构造哈希表;2)根据选择的冲突处理方法结局地址冲突;3)在哈希表的基础上实现哈希查找。
哈希函数的构造函数常用的有5种:数字分析法、平方取中法、分段叠加、伪随机数法、余数法(接下来的代码将采取最为常用的余数法)。
虽然通过构造好的哈希函数可以减少冲突,但是冲突是不可能完全避免的,所以就相应地产生了避免哈希冲突的四种方法,分别是:
1.开放定址法:1)线性探测再散列(接下来的代码将采取该方法);2)二次探测再散列。
2.链地址法。
3.再哈希法。
4.建立公共溢出区(公共溢出区问题我会在接下来的Win32编程的第三章中提及)。
开放定址法中的线性探测再散列比较常用,该方法的特点是冲突发生时,顺序查看表中的下一单元,直到找出一个空单元或者查遍全表。
代码:
1 #include <stdio.h>
2 #include <time.h>
3 #define Max 11
4 #define N 8
5 int hashtable[Max];
6 int func(int value)
7 {
8 return value % Max;
9 /*哈希函数*/
10 }
11 int search(int key)
12 /*自定义函数实现哈希查询*/
13 {
14 int pos, t;
15 pos = func(key);
16 /*哈希函数确定出的位置*/
17 t = pos;
18 /*t存放确定出的位置*/
19 while (hashtable[t] != key && hashtable[t] != - 1)
20 /*如果该位置上不等于要查找的关键字且不为空*/
21 {
22 t = (t + 1) % Max;
23 /*利用线性探测求出下一个位置*/
24 if (pos == t)
25 /*如果经多次探测又回到原来用哈希函数求出的位置则说明要查找的数不存在*/
26 return - 1;
27 }
28 if (hashtable[t] == - 1)
29 /*如果探测的位置是-1则说明要查找的数不存在*/
30 return NULL;
31 else
32 return t;
33 }
34 void creathash(int key)
35 /*自定义函数创建哈希表*/
36 {
37 int pos, t;
38 pos = func(key);
39 /*哈希函数确定元素的位置*/
40 t = pos;
41 while (hashtable[t] != - 1)
42 /*如果该位置有元素存在则进行线性探测再散列*/
43 {
44 t = (t + 1) % Max;
45 if (pos == t)
46 /*如果冲突处理后确定的位置与原位置相同则说明哈希表已满*/
47 {
48 printf("hash table is full\n");
49 return ;
50 }
51 }
52 hashtable[t] = key;
53 /*将元素放入确定的位置*/
54 }
55 main()
56 {
57 int flag[50];
58 int i, j, t;
59 for (i = 0; i < Max; i++)
60 hashtable[i] = - 1;
61 /*哈希表中初始位置全置-1*/
62 for (i = 0; i < 50; i++)
63 flag[i] = 0;
64 /*50以内所有数未产生时均标志为0*/
65 srand((unsigned long)time(0));
66 /*利用系统时间做种子产生随机数*/
67 i = 0;
68 while (i != N)
69 {
70 t = rand() % 50;
71 /*产生一个50以内的随机数赋给t*/
72 if (flag[t] == 0)
73 /*查看t是否产生过*/
74 {
75 creathash(t);
76 /*调用函数创建哈希表*/
77 printf("%2d:", t);
78 /*将该元素输出*/
79 for (j = 0; j < Max; j++)
80 printf("(%2d) ", hashtable[j]);
81 /*输出哈希表中内容*/
82 printf("\n");
83 flag[t] = 1;
84 /*将产生的这个数标志为1*/
85 i++;
86 /*i自加*/
87 }
88 }
89 printf("please input number which do you want to search:");
90 scanf("%d", &t);
91 /*输入要查找的元素*/
92 if (t > 0 && t < 50)
93 {
94 i = search(t);
95 /*调用search进行哈希查找*/
96 if (i != - 1)
97 printf("success!The position is:%d\n", i);
98 /*若查找到该元素则输出其位置*/
99 else
100 printf("sorry,no found!");
101 /*未找到输出提示信息*/
102 }
103 else
104 printf("inpput error!");
105 }
反思:哈希查找的难点在于两点:1.使用的方法难以迅速理解,造成记忆困难;2.其中可能采取的哈希函数、冲突解决方法不唯一。两者叠加,造成对哈希查找的忘却。
总结:至此,主要的四种查找方法都已经详细讲述了。需要按照顺序一步步理解,记忆。
4.4 其他重要算法
实例110 迪杰斯特拉算法
问题:通过迪杰斯特拉算法求解如图所示的顶点1到各顶点的的最短路径。
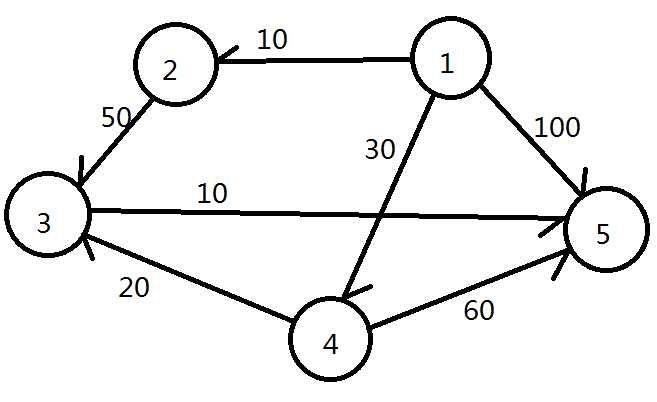
逻辑:迪杰斯特拉算法是一种图谱搜索算法。许多问题都可以建模为图谱,再通过这个算法计算出最短路径。其算法思想:设置并逐步扩充一个集合S,存放已求出其最短路径的顶点,则尚未确定最短路径的顶点集合是V-S(其中V是网中所有顶点集合)。按最短路径长度递增的顺序逐个将V-S中的顶点加到S中,直到S中包含全部顶点,而V-S为空。
代码:
1 #include<stdlib.h>
2 #include<stdio.h>
3 #define MAXNODE 30
4 #define MAXCOST 1000
5 int dist[MAXNODE],cost[MAXNODE][MAXNODE],n=5;
6 void dijkstra(int v0)
7 {
8 int s[MAXNODE];
9 int mindis,dis,i,j,u;
10 for(i=1;i<=n;i++)
11 {
12 dist[i]=cost[v0][i];
13 s[i]=0;
14 }
15 s[v0]=1;
16 for(i=1;i<=n;i++)
17 {
18 mindis=MAXCOST;
19 for(j=1;j<=n;j++)
20 if(s[j]==0&&dist[j]<mindis)
21 {
22 u=j;
23 mindis=dist[j];
24 }
25 s[u]=1;
26 for(j=1;j<=n;j++)
27 if(s[j]==0)
28 {
29 dis=dist[u]+cost[u][j];
30 dist[j]=(dist[j]<dis)?dist[j]:dis;
31 }
32 }
33 }
34 void display_path(int v0)
35 {
36 int i;
37 printf("\n 顶点 %d 到各顶点的最短路径长度如下:\n",v0);
38 for(i=1;i<=n;i++)
39 {
40 printf(" (v%d->v%d):",v0,i);
41 if(dist[i]==MAXCOST)
42 printf("wu lun jing\n");
43 else
44 printf("%d\n",dist[i]);
45 }
46 }
47 main()
48 {
49 int i,j,v0=1;
50 for(i=1;i<=n;i++)
51 for(j=1;j<=n;j++)
52 cost[i][j]=MAXCOST;
53 for(i=1;i<=n;i++)
54 cost[i][i]=0;
55 cost[1][2]=10;
56 cost[1][5]=100;
57 cost[1][4]=30;
58 cost[2][3]=50;
59 cost[4][3]=20;
60 cost[3][5]=10;
61 cost[4][5]=60;
62 dijkstra(v0);
63 display_path(v0);
64 }
反思:这个算法是上一章图论部分中特意留取下来的。这个算法在互联网、物流等多个方面有着其重要作用。
总结:其实还有许多算法这里都没有写到。这里只是写到一些基础算法。之后如果有时间的话,会单开章节写一些其他算法,诸如傅里叶变换于快速傅里叶变换等算法。
摘录: 八大排序算法 http://blog.csdn.net/hguisu/article/details/7776068
统治世界的十大算法 http://36kr.com/p/212499.html
百度图片、百度知道、百度百科、搜狗百科等
2016.10.03发布
标签:
原文地址:http://www.cnblogs.com/Tiancheng-Duan/p/5863410.html