标签:
1>类的对象实例化
由于main为静态类型,所以在调用函数时也必须调用静态方法,如上代码中的求平方数的静态方法,如何在静态main中调用非静态类的方法呢?
静态方法只能直接访问静态成员,无法访问非静态成员,如果想要访问费静态方法,则实例化该类对象,使用对象名.非静态方法()的方式来访问。
第一:创建类的对象
类名 对象名=new 类名( );
第二:调用方法或变量
对象名.成员方法名();
数据类型 变量名= 对象名.成员变量名;
2>编写一个方法,使用以上算法生成指定数目(比如1000个)的随机整数。
方法:通过置X(n + 1) ≡(a*X(n) + c )mod m ,求得随机数序列< Xn > , 这个序列称作线性同余序列。m、a 、c 和 X0 分别称做模数、乘数、增量和初始值。
模m, m > 0
系数a, 0 < a < m
增量c, 0 <= c < m
原始值(种子) 0 <= X(0) < m
import java.util.*; public class TextRandom { public static void main(String[] args) { // TODO Auto-generated method stub Scanner in = new Scanner(System.in); int a = (int)Math.pow(7,5); int m = (int)Math.pow(2, 31) - 1; int c = 0; System.out.print("请输入要产生随机数的个数:"); int n = in.nextInt(); for(int i = 0;i<n;i++) { Random x1 = new Random(); int x3 = x1.nextInt(10); int x2 = (a* x3+c)%m; System.out.println(x2); } } }
方法重载:
3>请看以下代码,你发现了有什么特殊之处吗?
1 // MethodOverload.java 2 // Using overloaded methods 3 4 public class MethodOverLoad { 5 6 public static void main(String[] args) { 7 System.out.println("The square of integer 7 is " + square(7)); 8 System.out.println("\nThe square of double 7.5 is " + square(7.5)); 9 } 10 11 public static int square(int x) { 12 return x * x; 13 } 14 15 public static double square(double y) { 16 return y * y; 17 } 18 }
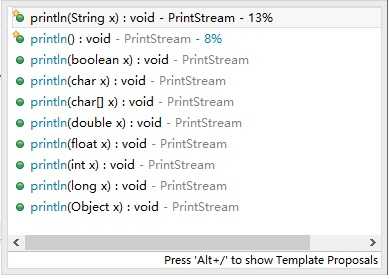
上诉代码显示了 Java 的“方法重载”特性,上诉代码由于方法的参数类型不同(一个为 int,一个为 double ),使同名的函数被调用时有所区分;满足以下条件的两个或多个方法构成“重载”关系: 方法名相同, 参数类型不同,参数个数不同,或参数类型的顺序不同;但方法的返回值不作为方法重载的判断条件。例如在JDK中调用 System.out.println() 函数时会显示许多重载函数。
4>使用计算机计算组合数:
(1)使用组合数公式利用n!来计算![]()
1 //利用阶乘公式计算组合数 2 import java.util.*; 3 public class CombinationNumber { 4 5 public static void main(String[] args) { 6 // TODO Auto-generated method stub 7 Scanner in = new Scanner(System.in); 8 System.out.print("请输入组合数下标n:"); 9 int n = in.nextInt(); 10 System.out.print("请输入组合数上标k:"); 11 int k = in.nextInt(); 12 13 int C = Jiecheng(n)/(Jiecheng(k)*Jiecheng(n - k)); 14 System.out.println("C(n,k) = "+C); 15 16 } 17 public static int Jiecheng(int n)//递归法计算阶乘 18 { 19 int s = 0; 20 if(n < 0) 21 System.out.println("Error!"); 22 else if(n == 1||n == 0) 23 s = 1; 24 else 25 s = n * Jiecheng(n -1); 26 return s; 27 } 28 }


实验总结:利用递归法求阶乘,利用公式即可求得组合数的计算结果。
(2)使用递推的方法用杨辉三角形计算![]()
1 //使用递推的方法用杨辉三角形计算组合数 2 import java.util.Scanner; 3 4 public class CombinationNumber2 { 5 6 public static void main(String[] args) { 7 // TODO Auto-generated method stub 8 Scanner in = new Scanner(System.in); 9 System.out.print("请输入组合数下标n:"); 10 int n = in.nextInt(); 11 System.out.print("请输入组合数上标k:"); 12 int k = in.nextInt(); 13 14 int C = CombinationNumber(n,k); 15 System.out.println("C(n,k) = "+C); 16 } 17 public static int CombinationNumber(int n,int k) 18 { 19 if(k == 0||n == k) return 1; 20 int s=Math.min(k,n-k); 21 int p = 1,q = 0; 22 23 for(int i = 1; i <= s; i++)//递推计算 24 { 25 q = p * (n-i+1)/(i); 26 p = q; 27 } 28 29 return q; 30 } 31 }


实验总结:利用for循环逐步求得组合数结果。
(3)使用递归的方法用组合数递推公式计算![]()
//使用递归的方法用组合数递推公式计算 import java.util.Scanner; public class CombinationNumber3 { public static void main(String[] args) { // TODO Auto-generated method stub Scanner in = new Scanner(System.in); System.out.print("请输入组合数下标n:"); int n = in.nextInt(); System.out.print("请输入组合数上标k:"); int k = in.nextInt(); int C = CombinationNumber(n,k); System.out.println("C(n,k) = "+C); } public static int CombinationNumber(int n,int k)//递归法计算组合数 { int c = 0; if(n == 1||k == 0||n == k) c = 1; else c = CombinationNumber(n - 1,k - 1) + CombinationNumber(n - 1,k); return c; } }


实验总结:利用递推公式,递归方式求得;注意结束条件。
5>递归编程解决汉诺塔问题,用Java实现。
//递归编程解决汉诺塔问题。
import java.util.*;
public class TowersOfHanoi2 {
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner in = new Scanner(System.in);
System.out.print("请输入盘子个数:");//盘子从上至下编号从1到n
int p = in.nextInt();
char ch1 = ‘A‘;
char ch2 = ‘B‘;
char ch3 = ‘C‘;
Hanoi(p,ch1,ch2,ch3);//最终实现1到n个盘子从A柱移到C柱
}
public static void move(int n,char from,char to)
{
System.out.printf( "将%d号盘子%c --> %c\n",n,from,to);
}
public static void Hanoi(int n,char from,char mid,char to)
{
if(n == 1)
move(1,from,to);//结束条件,当n = 1时移动一次即可
else
{Hanoi(n-1,from,to,mid);//将n-1个盘子从A移到B
move(n,from,to);//将n个盘子移到C
Hanoi(n-1,mid,from,to);//将n-1个盘子从B移到C
}
}
}
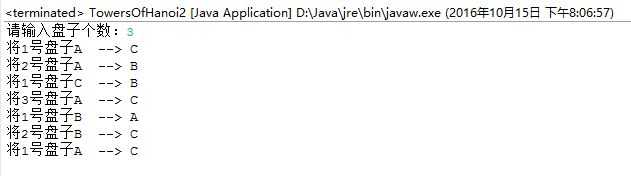
实验总结: 当A塔上有n个盘子时,先将A塔上编号 1 至 n-1 的盘子移动到B塔上(借助C塔),然后将A塔上n号盘子移动到C塔上,最后将B塔上的n-1个盘子借助A塔移动到C塔上。即用递归实现,结束条件是 n=1 时只需直接移动;遇到的问题:如何递归实现。
6>使用递归方式判断某个字串是否是回文。
//判断输入的字符串是否是回文数 import java.util.*; public class Huiwen { public static void main(String[] args) { // TODO Auto-generated method stub String temp = ""; char[] a; Scanner in = new Scanner(System.in); System.out.print("请输入要判断的字符串:"); String str = in.next(); a = str.toCharArray();//将字符串对象中的字符转换为一个字符数组 for(int i = a.length - 1;i >= 0;i--)//将字符串逆置 { temp += a[i]; } if(str.equals(temp)) System.out.println(str+"是回文数!"); else System.out.println(str+"不是回文数!"); } }



实验总结:将输入的字符串转化为数组形式储存才能方便比较(利用 toCharArray() 函数)。
标签:
原文地址:http://www.cnblogs.com/ttzz/p/5962333.html