标签:当前时间 recursion 方法 length exp test size lap 误差
本篇文章解决的问题来源于算法设计与分析课程的课堂作业,主要是运用多种方法来计算斐波那契数。具体问题及解法如下:
问题描述:利用迭代算法寻找不超过编程环境能够支持的最大整数的斐波那契数是第几个斐波那契数。(Java: 231-1 for int, 263-1 for long)
解决方案:针对问题1,此处要使用迭代法来解决,具体实现代码如下:
//用迭代法寻找编程环境支持的最大整数(int型)的斐波那契数是第几个斐波那契数 public static int max_int_iteration(){ int a = 1,b = 1,c = 2; int count = 3; for( ;b < c; ){ //一旦c达到编程环境最大斐波那契数,便会产生内存溢出,从而变成一个负数,到此循环结束 a = b; b = c; c = a + b; count++; } return count; } //用迭代法寻找编程环境支持的最大整数(long型)的斐波那契数是第几个斐波那契数 public static long max_long_iteration(){ long a = 1,b = 1,c = 2; long count = 3; for( ;b<c; ){ //一旦c达到编程环境最大斐波那契数,便会产生内存溢出,从而变成一个负数,到此循环结束 a = b; b = c; c = a + b; count++; } return count; }
问题描述:根据问题1中计算的最大的斐波那契数序号n,采用递归方式计算第n个斐波那契数,看其是否可以在3分钟内完成。
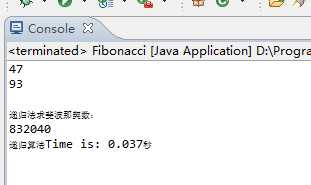
解决方案:针对问题2,此处要使用递归法来解决,问题1实际运行结果为:支持的最大整数(int型)值为47,支持的最大整数(long型)值为93。使用递归法计算第47个斐波那契数实际所需时间为138秒左右(此处本人使用WIN7系统运行所得),具体实现代码如下:
//递归法 public static long recursion(long n){ long result = 0; //最后一个斐波那契数及存储中间斐波那契数的变量 if(n <= 0) result = 0; if(n == 1 || n == 2) result = 1; if(n > 2) { result = recursion(n-1) + recursion(n-2); //System.out.print(result+" "); } return result; } //具体实现就只需使用System.currentTimeMillis()方法获取系统当前时间,就可以你计算出计算第47个斐波那契数所需时间
问题描述:利用递归算法计算你的计算机能够在1,5,10,50秒内计算出的最大斐波那契数是第几个,利用迭代算法求解同样的问题。
解决方案:针对问题3,此处先要了解获得系统当前时间的相关方法及用法,然后计算规定时间内计算出的最大斐波那契数就很简单啦,具体实现代码如下:
//在1,5,10,50秒内使用迭代法算出的最大斐波那契数是第几个 public static void time_iteration(){ int a = 1,b = 1,c = 2; long count = 3; long a1 = 0,a2 = 0,a3 = 0,a4 = 0; long t1 = System.currentTimeMillis(); long t2 = System.currentTimeMillis(); for( ;t2-t1 < 60000; ){ a = b; b = c; c = a + b; count++; t2 = System.currentTimeMillis(); if(t2-t1 == 1000) a1 = count; //System.out.println("1秒内最大斐波那契数是第:"+count+"个 "); if(t2-t1 == 5000) a2 = count; //System.out.println("5秒内最大斐波那契数是第:"+count+"个 "); if(t2-t1 == 10000) a3 = count; //System.out.println("10秒内最大斐波那契数是第:"+count+"个 "); if(t2-t1 == 50000) a4 = count; //System.out.println("50秒内最大斐波那契数是第:"+count+"个 "); } System.out.println("迭代法1秒内最大斐波那契数是第:"+a1+"个 "); System.out.println("迭代法5秒内最大斐波那契数是第:"+a2+"个 "); System.out.println("迭代法10秒内最大斐波那契数是第:"+a3+"个 "); System.out.println("迭代法50秒内最大斐波那契数是第:"+a4+"个 "); } //递归法 public static long recursion(long n){ long result = 0; //最后一个斐波那契数及存储中间斐波那契数的变量 if(n <= 0) result = 0; if(n == 1 || n == 2) result = 1; if(n > 2) { result = recursion(n-1) + recursion(n-2); //System.out.print(result+" "); } return result; } //规定时间内,递归法计算出的最大斐波那契数是第几个 public static int recursion_time(long time){ long starttime_dg=System.currentTimeMillis(); int i=3; long endtime_dg=0; while(endtime_dg<starttime_dg+time*1000){ endtime_dg=System.currentTimeMillis(); i++; recursion(i); } return i; } //递归法在1,5,10,50秒内算出的最大斐波那契数是第几个 public static void fbnq_recursion_time(){ System.out.println("1秒内最大斐波那契数是第:"+recursion_time(1)+"个 "); System.out.println("5秒内最大斐波那契数是第:"+recursion_time(5)+"个 "); System.out.println("10秒内最大斐波那契数是第:"+recursion_time(10)+"个 "); System.out.println("50秒内最大斐波那契数是第:"+recursion_time(50)+"个 "); }
问题描述:利用公式F(n) = [fn/sqrt(5)]快速计算第n个斐波那契数,找出出现误差时的最小n值。其具体公式描述见下图:

解决方案:针对问题4,只需要将上述公式用代码来描述就可以完成,具体实现代码如下:
//直接求值法(利用公式F(n) = [@n/sqrt(5)]快速计算第n个斐波那契数) public static double formula(int n){ double result = 0; double temp = Math.sqrt(5.0); result = (1/temp)*(Math.pow((1+temp)/2,n)-Math.pow((1-temp)/2, n)); return result; }
问题描述:利用矩阵相乘方法计算第n个斐波那契数。
解决方案:对于矩阵相乘法,首先得对矩阵相乘的法则要熟悉,本人在实现此功能时,也没完全吃透矩阵相乘中的核心思想,实现代码参考于网上一篇博客(PS:具体链接:http://blog.csdn.net/u010786672/article/details/44678769),具体实现代码如下:
// 关联矩阵 private static final int[][] UNIT = { { 1, 1 }, { 1, 0 } }; // 全0矩阵 private static final int[][] ZERO = { { 0, 0 }, { 0, 0 } }; /** * 求斐波那契数列 * * @param n * @return */ public static int[][] fb(int n) { if (n == 0) { return ZERO; } if (n == 1) { return UNIT; } // n是奇数 if ((n & 1) == 0) { int[][] matrix = fb(n >> 1); return matrixMultiply(matrix, matrix); } // n是偶数 int[][] matrix = fb((n - 1) >> 1); return matrixMultiply(matrixMultiply(matrix, matrix), UNIT); } /** * 矩阵相乘 * * @param m * r1*c1 * @param n * c1*c2 * @return 新矩阵,r1*c2 */ public static int[][] matrixMultiply(int[][] m, int[][] n) { int rows = m.length; int cols = n[0].length; int[][] r = new int[rows][cols]; for (int i = 0; i < rows; i++) { for (int j = 0; j < cols; j++) { r[i][j] = 0; for (int k = 0; k < m[i].length; k++) { r[i][j] += m[i][k] * n[k][j]; } } } return r; } //具体实现矩阵相乘算法 public static int matrix(int n){ int[][] m = fb(n); return m[0][1]; }
问题描述:对于相同的输入n值,比较上述四种方法的基本操作次数,以掌握对数、线性和指数增长率的极大差别。
解决方案:此处本人只是把上述所用的四种方法运行了一遍,计算各个相应方案计算第n个斐波那契数所花时间,因为具体算法相应的基本操作次数,用代码来计算有点麻烦,所以此处就不罗列了。
这是解决斐波那契数的一种新算法,该算法的时间和空间效率都优于上面四种算法,该算法所用公式如下图所示:

具体实现代码如下:
//新算法法 public static int new_way(int n){ //int a = 1,b = 1,c = 2,d = 3; int result = 0; //定义最后一个斐波那契数 //根据输入n,求出最后一个斐波那契数 if(n == 0) result = 0; else if(n == 1 || n == 2) result = 1; else if(n == 3) result = 2; else if(n >= 4){ //若n大于4返回resul int a1 = n/4; int b1 = n%4; int a = new_way(a1); int b = new_way((a1+1)); int c = new_way((a1-1)); int d = new_way((a1+2)); if(b1 == 0) result = (int) ((Math.pow(b,2) - Math.pow(c,2))*(Math.pow(c, 2) + 2*Math.pow(a, 2) + Math.pow(b,2))); if(b1 == 1) result = (int) (Math.pow((Math.pow(b,2) - Math.pow(c,2)),2) + Math.pow((Math.pow(a, 2) + Math.pow(b,2)),2)); if(b1 == 2) result = (int) ((Math.pow(a, 2) + Math.pow(b,2))*(3*Math.pow(b,2)+Math.pow(a, 2)-2*Math.pow(c,2))); if(b1 == 3) result = (int) (Math.pow((Math.pow(a, 2) + Math.pow(b,2)),2) + Math.pow((Math.pow(d,2)-Math.pow(a,2)),2)); } return result; }
代码如下:

1 package com.liuzhen.ex_one; 2 3 public class Fibonacci { 4 5 //迭代法 6 public static int iteration(int n){ /*此处(包含下面所有方法)声明为静态方法,原因是在本类main()方法中调用 7 类中方法,对于一般的非static成员变量或方法,需要有一个对象的实例才能调用,所以要先生成对象的实例,他们才会实际的分配内存空间。 8 而对于static的对象或方法,在程序载入时便已经分配了内存空间,他只和特定的类想关联,无需实例化 */ 9 int result = 1; //最后一个斐波那契数 10 int a[] = new int[n+1]; //存放斐波那契数,初始值为空,默认全为0 11 a[0] = 0; 12 a[1] = 1; 13 //System.out.println("迭代法计算斐波那契数结果:"); 14 //System.out.print(a[0]+" "+a[1]+" "); 15 for(int i = 2;i < n+1;i++){ 16 a[i] = a[i-1] + a[i-2]; 17 //result = a[i]; 18 //System.out.print(result+" "); //打印斐波那契数 19 } 20 //System.out.println(); 21 result=a[n]; 22 return result; //返回最后一个斐波那契数 23 } 24 25 //用迭代法寻找编程环境支持的最大整数(int型)的斐波那契数是第几个斐波那契数 26 public static int max_int_iteration(){ 27 int a = 1,b = 1,c = 2; 28 int count = 3; 29 for( ;b < c; ){ //一旦c达到编程环境最大斐波那契数,便会产生内存溢出,从而变成一个负数,到此循环结束 30 a = b; 31 b = c; 32 c = a + b; 33 count++; 34 } 35 return count; 36 } 37 38 39 //用迭代法寻找编程环境支持的最大整数(long型)的斐波那契数是第几个斐波那契数 40 public static long max_long_iteration(){ 41 long a = 1,b = 1,c = 2; 42 long count = 3; 43 for( ;b<c; ){ //一旦c达到编程环境最大斐波那契数,便会产生内存溢出,从而变成一个负数,到此循环结束 44 a = b; 45 b = c; 46 c = a + b; 47 count++; 48 } 49 return count; 50 } 51 52 //在1,5,10,50秒内使用迭代法算出的最大斐波那契数是第几个 53 public static void time_iteration(){ 54 int a = 1,b = 1,c = 2; 55 long count = 3; 56 long a1 = 0,a2 = 0,a3 = 0,a4 = 0; 57 long t1 = System.currentTimeMillis(); 58 long t2 = System.currentTimeMillis(); 59 for( ;t2-t1 < 60000; ){ 60 a = b; 61 b = c; 62 c = a + b; 63 count++; 64 t2 = System.currentTimeMillis(); 65 if(t2-t1 == 1000) 66 a1 = count; 67 //System.out.println("1秒内最大斐波那契数是第:"+count+"个 "); 68 if(t2-t1 == 5000) 69 a2 = count; 70 //System.out.println("5秒内最大斐波那契数是第:"+count+"个 "); 71 if(t2-t1 == 10000) 72 a3 = count; 73 //System.out.println("10秒内最大斐波那契数是第:"+count+"个 "); 74 if(t2-t1 == 50000) 75 a4 = count; 76 //System.out.println("50秒内最大斐波那契数是第:"+count+"个 "); 77 } 78 System.out.println("迭代法1秒内最大斐波那契数是第:"+a1+"个 "); 79 System.out.println("迭代法5秒内最大斐波那契数是第:"+a2+"个 "); 80 System.out.println("迭代法10秒内最大斐波那契数是第:"+a3+"个 "); 81 System.out.println("迭代法50秒内最大斐波那契数是第:"+a4+"个 "); 82 } 83 84 //递归法 85 public static long recursion(long n){ 86 long result = 0; //最后一个斐波那契数及存储中间斐波那契数的变量 87 if(n <= 0) 88 result = 0; 89 if(n == 1 || n == 2) 90 result = 1; 91 if(n > 2) 92 { 93 result = recursion(n-1) + recursion(n-2); 94 //System.out.print(result+" "); 95 } 96 return result; 97 } 98 99 //规定时间内,递归法计算出的最大斐波那契数是第几个 100 public static int recursion_time(long time){ 101 long starttime_dg=System.currentTimeMillis(); 102 int i=3; 103 long endtime_dg=0; 104 while(endtime_dg<starttime_dg+time*1000){ 105 endtime_dg=System.currentTimeMillis(); 106 i++; 107 recursion(i); 108 } 109 return i; 110 } 111 112 //递归法在1,5,10,50秒内算出的最大斐波那契数是第几个 113 public static void fbnq_recursion_time(){ 114 115 System.out.println("1秒内最大斐波那契数是第:"+recursion_time(1)+"个 "); 116 117 System.out.println("5秒内最大斐波那契数是第:"+recursion_time(5)+"个 "); 118 119 System.out.println("10秒内最大斐波那契数是第:"+recursion_time(10)+"个 "); 120 121 System.out.println("50秒内最大斐波那契数是第:"+recursion_time(50)+"个 "); 122 123 124 } 125 126 //测试递归法在1,5,10,50秒内使用迭代法算出的最大斐波那契数是第几个 127 public static void time_recursion_test(){ 128 long t1 = System.currentTimeMillis(); 129 long t2 = 0; 130 int i = 3; 131 for(;t2-t1 > 60000;){ 132 recursion(i); 133 i++; 134 t2 = System.currentTimeMillis(); 135 if(t2-t1 == 1000) 136 System.out.println("1秒内最大斐波那契数是第:"+i+"个 "); 137 if(t2-t1 == 5000) 138 System.out.println("5秒内最大斐波那契数是第:"+i+"个 "); 139 if(t2-t1 == 10000) 140 System.out.println("10秒内最大斐波那契数是第:"+i+"个 "); 141 if(t2-t1 == 50000) 142 System.out.println("50秒内最大斐波那契数是第:"+i+"个 "); 143 144 } 145 } 146 147 //直接求值法(利用公式F(n) = [@n/sqrt(5)]快速计算第n个斐波那契数) 148 public static double formula(int n){ 149 double result = 0; 150 double temp = Math.sqrt(5.0); 151 result = (1/temp)*(Math.pow((1+temp)/2,n)-Math.pow((1-temp)/2, n)); 152 return result; 153 } 154 155 156 //利用直接求值法,出现误差时最小的n值 157 public static int min_formula(){ 158 double result_fn=1; 159 int i=1; 160 while(result_fn-(double)iteration(i)<1){ 161 result_fn=formula(i); 162 i++; 163 } 164 return i; 165 } 166 167 //新算法法 168 public static int new_way(int n){ 169 //int a = 1,b = 1,c = 2,d = 3; 170 int result = 0; //定义最后一个斐波那契数 171 //根据输入n,求出最后一个斐波那契数 172 if(n == 0) 173 result = 0; 174 else if(n == 1 || n == 2) 175 result = 1; 176 else if(n == 3) 177 result = 2; 178 else if(n >= 4){ //若n大于4返回resul 179 int a1 = n/4; 180 int b1 = n%4; 181 int a = new_way(a1); 182 int b = new_way((a1+1)); 183 int c = new_way((a1-1)); 184 int d = new_way((a1+2)); 185 if(b1 == 0) 186 result = (int) ((Math.pow(b,2) - Math.pow(c,2))*(Math.pow(c, 2) + 2*Math.pow(a, 2) + Math.pow(b,2))); 187 if(b1 == 1) 188 result = (int) (Math.pow((Math.pow(b,2) - Math.pow(c,2)),2) + Math.pow((Math.pow(a, 2) + Math.pow(b,2)),2)); 189 if(b1 == 2) 190 result = (int) ((Math.pow(a, 2) + Math.pow(b,2))*(3*Math.pow(b,2)+Math.pow(a, 2)-2*Math.pow(c,2))); 191 if(b1 == 3) 192 result = (int) (Math.pow((Math.pow(a, 2) + Math.pow(b,2)),2) + Math.pow((Math.pow(d,2)-Math.pow(a,2)),2)); 193 194 } 195 return result; 196 } 197 198 199 // 关联矩阵 200 private static final int[][] UNIT = { { 1, 1 }, { 1, 0 } }; 201 // 全0矩阵 202 private static final int[][] ZERO = { { 0, 0 }, { 0, 0 } }; 203 /** 204 * 求斐波那契数列 205 * 206 * @param n 207 * @return 208 */ 209 public static int[][] fb(int n) { 210 if (n == 0) { 211 return ZERO; 212 } 213 if (n == 1) { 214 return UNIT; 215 } 216 // n是奇数 217 if ((n & 1) == 0) { 218 int[][] matrix = fb(n >> 1); 219 return matrixMultiply(matrix, matrix); 220 } 221 // n是偶数 222 int[][] matrix = fb((n - 1) >> 1); 223 return matrixMultiply(matrixMultiply(matrix, matrix), UNIT); 224 } 225 226 /** 227 * 矩阵相乘 228 * 229 * @param m 230 * r1*c1 231 * @param n 232 * c1*c2 233 * @return 新矩阵,r1*c2 234 */ 235 public static int[][] matrixMultiply(int[][] m, int[][] n) { 236 int rows = m.length; 237 int cols = n[0].length; 238 int[][] r = new int[rows][cols]; 239 for (int i = 0; i < rows; i++) { 240 for (int j = 0; j < cols; j++) { 241 r[i][j] = 0; 242 for (int k = 0; k < m[i].length; k++) { 243 r[i][j] += m[i][k] * n[k][j]; 244 } 245 } 246 } 247 return r; 248 } 249 250 //具体实现矩阵相乘算法 251 public static int matrix(int n){ 252 int[][] m = fb(n); 253 return m[0][1]; 254 } 255 256 public static void main(String[] args){ 257 System.out.print(max_int_iteration()); 258 System.out.println(); 259 System.out.print(max_long_iteration()); 260 System.out.println(); 261 System.out.println(); 262 long t1 = System.currentTimeMillis(); 263 long a = recursion(47); 264 long t2 = System.currentTimeMillis(); 265 System.out.println("递归法求斐波那契数:"); 266 System.out.println(a); 267 System.out.println("递归算法Time is: " + (t2 - t1)/1000.0+"秒"); 268 269 //此处下面可以直接通过给相关类传递参数,实现相应功能,上面的中代码仅仅提供示例 270 } 271 272 }
PS:运行部分结果截图
本文具体代码主要参考于下面一篇博客:http://blog.csdn.net/u011181633/article/details/46353181
标签:当前时间 recursion 方法 length exp test size lap 误差
原文地址:http://www.cnblogs.com/liuzhen1995/p/6014322.html