标签:figure com 不同 元素 更新 矩阵 center title sig
P0问题求解相关算法
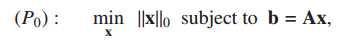
1.OMP
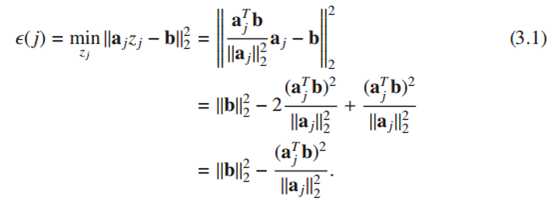
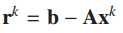
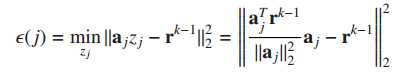
搜寻最小误差即求<>的最大值
对误差求导,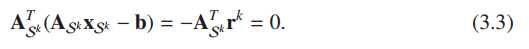
即, A中对应SS的列与残差正交。
算法步骤:
输入稀疏向量x(m*1),列归一化矩阵A(n*m),理想输出b,稀疏度K,误差精度
初始化残差r1为b
找到A‘*r1的最大值所在索引posZ(列索引,有相对应的x的元素)
更新索引向量SS=sort([SS,posZ(1)])
找到||A(:,SS)x-b||最小二乘解x0= pinv(A(:,SS))*b
求残差r1=b-A(:,SS)*x0= b-A(:,SS)* pinv(A(:,SS))*b,
(这里可以理解为【b-b在A(:,SS)上的正交投影】,A(:,SS)* pinv(A(:,SS))为正交投影算子,因此下一次寻找索引时SS所在列不会再次选入)
while迭代直到残差满足条件(可多次循环)
输出向量为x0,求误差r2(利用2范数norm)2.LS-OMP
与OMP不同之处在于索引posZ的搜索:
对A的所有累积的列和备选的一列求残差r1,索引posZ则为残差最小的一列,后面步骤相同
n=20;m=30;
A=randn(n,m);
W=sqrt(diag(A‘*A));
for k=1:1:m
A(:,k)=A(:,k)/W(k);
end
for S=1:1:10
for ex=1:1:50
x=zeros(m,1);
pos=randperm(m);
x(pos(1:S))=sign(randn(S,1)).*(1+rand(S,1)); %x的稀疏度为S,即稀疏度逐渐增加到Smax
b=A*x;
thrLSMP=1e-4;
%LS-OMP
r=b;
SS=[];
while r‘*r>thrLSMP
z=zeros(m,1);
for j=1:1:m
rtemp=b-A(:,[SS,j])*pinv(A(:,[SS,j]))*b;
z(j)=rtemp‘*rtemp;
end
posZ=find(z==min(z),1);
SS=[SS,posZ(1)];
r=b-A(:,SS)*pinv(A(:,SS))*b;
end
x0=zeros(m,1);
x0(SS)=pinv(A(:,SS))*b;
r0(S,ex)=mean((x0-x).^2)/mean(x.^2);
%OMP
r=b;
SS=[];
while r‘*r>thrLSMP
z=abs(A‘*r);
posZ=find(z==max(z),1);
SS=[SS,posZ];
r=b-A(:,SS)*pinv(A(:,SS))*b;
end
x0=zeros(m,1);
x0(SS)=pinv(A(:,SS))*b;
r1(S,ex)=mean((x0-x).^2)/mean(x.^2);
end
end
figure(1);
plot(1:10,mean(r0(:,:),2),‘r-‘);hold on;
plot(1:10,mean(r1(:,:),2),‘k-‘);
legend(‘ls-OMP‘,‘OMP‘);
xlabel(‘K=1:10‘);
ylabel(‘err‘);
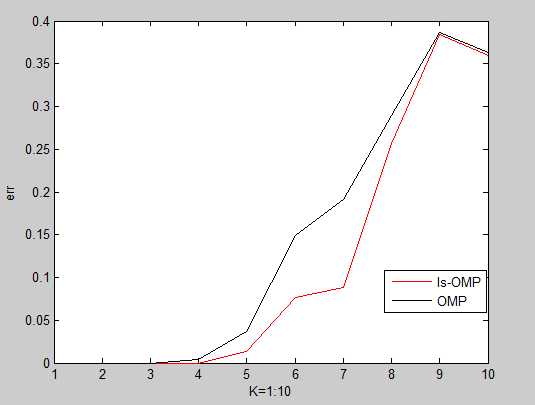
3.MP
与OMP不同之处在于残差的更新,MP不对索引值进行保留和更新,而是通过当前找到的一个索引值posZ(不是累积的SS)求残差,并更新输出向量xMP(posZ)=xMP(posZ)+A(:,posZ)‘*r1;
注:在正交匹配追踪OMP中,对应SS的A的列(即所有曾被选为posZ对应的列)均与残差正交,故不会被再次选为posZ,所以能保证快速收敛;而在MP中,只能保证上一步索引值对应的列与残差正交。
4. 阈值算法
OMP的简化版本。仅根据第一个投影取出索引值posZ,即
Z=A‘*b;
[Za,posZ]=sort(abs(Z),‘descend‘);
5. IRLS-noNoise
该算法与P1问题的IRLS比较接近,但该算法着重于l0范数的松弛,即lp(0<p<=1)。另外,与IRLS:|b-Ax|< 不同(利用最小二乘,即残差平方和),IRLS-noNoise针对的b=Ax(利用拉格朗日乘子,即直接求导等于0),即无噪声情况。
该算法可用于FOCUSS(两者有什么不同吗?。。。。)
同样的,引入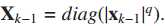
不可逆,则=
注:在后面的计算中,都不使用逆,而是伪逆
P0问题转换为M问题:q=1时,即P0问题;q=0.5时,即P1问题



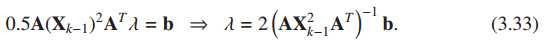
用伪逆代替逆:
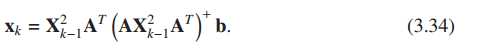
然后迭代一定次数即可得到比较好的解。
n=20;m=30;
A=randn(n,m);
W=sqrt(diag(A‘*A));
for k=1:1:m
A(:,k)=A(:,k)/W(k);
end
for S=1:1:10
x=zeros(m,1);
pos=randperm(m);
x(pos(1:S))=sign(randn(S,1)).*(1+rand(S,1)); %x的稀疏度为S,即稀疏度逐渐增加到Smax
b=A*x;
for k=1:1:20
%IRLS—noNoise
p=1;%l0 norm
%p=0.5; l1 norm
XX=diag(abs(x).^p);
XX2=XX*XX;
x0=XX2*A‘*pinv(A*XX2*A‘)*b;
rr3(k)=mean((x0-x).^2)/mean(x.^2);
end
r3(S)=rr3(20);
end
plot(r3);
title(‘err of IRLS-noNOISE‘);
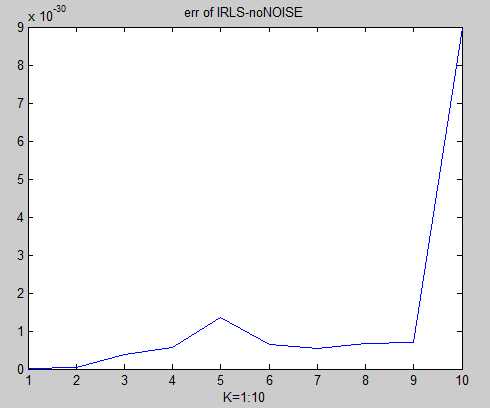
注:IRLS运行速度很快,而且可以实现很小的误差,是P0问题比较好的解法。
标签:figure com 不同 元素 更新 矩阵 center title sig
原文地址:http://www.cnblogs.com/fanmu/p/6061180.html