标签:归一化 学习 within [1] std rand center 技术 from
本人小白,第一次发布博客,大神绕路,不喜勿喷。
最近公司要求一些机器学习的内容,所以在看一些机器学习有关的资料,最近看的书名字叫做 机器学习实战。这是一本不错的书籍,很值得一读。
好,不说废话,进入我们今天的正题。
k-均值算法(k-means算法)
1.k-means算法是一种聚类算法。
何为聚类?聚类就是你在分类之前并不知道有几类,也不知道分别是哪几类,而让计算机根据数据的特征分成不同的几个类别,这些类别没有进行事先定义。这种分类方法又被称为无监督分类。
2.算法思想
在数据集中随机选取k个初始点作为质心,将数据集中的每一个点分配到一个簇中,为每个点找距离其最近的质心,将其分配到该质心所对应的簇,这一步完成之后,每个簇的质心更新为该簇所有点的平均值。到这里初始质心已经发生变化,重复以上步骤n次直到之心不再发生变化为止。
3.Python实现
# coding=utf-8
from numpy import *
import matplotlib
import matplotlib.pyplot as plt
import operator
from os import listdir
import time
初始化数据集
def createDataSet():
group = array([[1.0, 1.1], [1.0, 1.0],
[0, 0], [0, 0.1],
[2, 1.0], [2.1, 0.9],
[0.3, 0.0], [1.1, 0.9],
[2.2, 1.0], [2.1, 0.8],
[3.3, 3.5], [2.1, 0.9],
[2, 1.0], [2.1, 0.9],
[3.5, 3.4], [3.6, 3.5]
])
return group
#自己写的画图函数,每次都会画出初始数据集的点(红色),和要观察的点。
def show(data,color=None):
if not color:
color=‘green‘
group=createDataSet()
fig = plt.figure(1)
axes = fig.add_subplot(111)
axes.scatter(group[:, 0], group[:, 1], s=40, c=‘red‘)
axes.scatter(data[:, 0], data[:, 1], s=50, c=color)
plt.show()
代码取自机器学习实战第二章,在此加上我对这些代码的理解
def distEclud(vecA, vecB):
return sqrt(sum(power(vecA - vecB, 2))) #计算两点之间的欧氏距离
由于数据量级之间的差异会对影响度造成干扰,所以要对初始数据做数据归一化处理。
def randCent(dataSet, k): #数据归一化处理
n = shape(dataSet)[1]
centroids = mat(zeros((k, n))) # create centroid mat
for j in range(n): # create random cluster centers, within bounds of each dimension
minJ = min(dataSet[:, j])
rangeJ = float(max(dataSet[:, j]) - minJ)
centroids[:, j] = mat(minJ + rangeJ * random.rand(k, 1))
return centroids
shape(dataSet)是numpy库的一个方法,返回的是一个n维矩阵依次的维度。比如dataset=[[1,2,3],[2,4,5]] 的话,那么shape(dataset)=(2,3)
mat 方法是初始化矩阵
接下来是kmeans函数
def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent): #参数dataSet是待聚类数据矩阵,k是聚类类数
m = dataSet.shape[0] #训练集中含有点的个数
clusterAssment = zeros((m, 2)) #初始化结果集,个数等于训练集中点的个数
centroids = createCent(dataSet, k)
# print centroids
# show(centroids) #matplotlib画图展示训练数据分布
clusterChanged = True #标记参数,用来检测每次循环后质心位置是否还会发生变化
while clusterChanged:
clusterChanged = False
for i in range(m):
point = dataSet[i, :] # 遍历数据集中的每个点
mindist = inf #inf 是Python中的正无穷
minindex = -1 #随机定义一个序号,此序号用来表示每个点与哪个质心的距离最近,是质心的序号,初始随便取个负数就好
for n in range(k):
heart = centroids[n, :] # 遍历每个质心
distance = distMeas(point, heart) # 求点与质心距离
if distance < mindist: #如果此质心的距离比当前最小距离小
mindist = distance # 更新最小距离mindist
minindex = n # 更新最小距离的质心序号
if clusterAssment[i, 0] != minindex: clusterChanged = True 如果质心的序号发生变化,改变标记数据
clusterAssment[i, :] = minindex, mindist ** 2 # 将第i个点存为(最近质心序号,此点到质心距离的平方)
# print clusterAssment
for cent in range(k):#遍历数据集,更新质心的位置
ptsInClust = dataSet[(clusterAssment[:, 0] == cent)] # 取出该质心绑定的点
# print ptsInClust
if len(ptsInClust):
centroids[cent, :] = mean(ptsInClust, axis=0) # 取出点的均值
else:
centroids[cent, :] = array([[0, 0]])
show(centroids,color=‘green‘) #作图画出此次循环后质心的变化情况
# print centroids
# print "----------------"
# show(centroids)
return centroids, clusterAssment #返回质心,以及各个点的信息
centroids, clusterAssment=kMeans(createDataSet(),4) #聚类为4类
show(centroids,color=‘yellow‘) #聚类结果展示为黄色点
图片
初始数据集以及初始随机选取质心
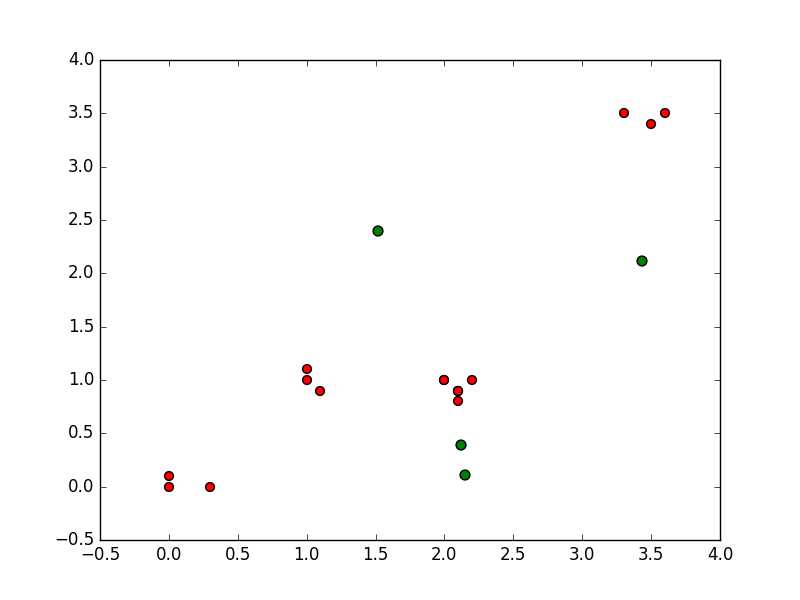
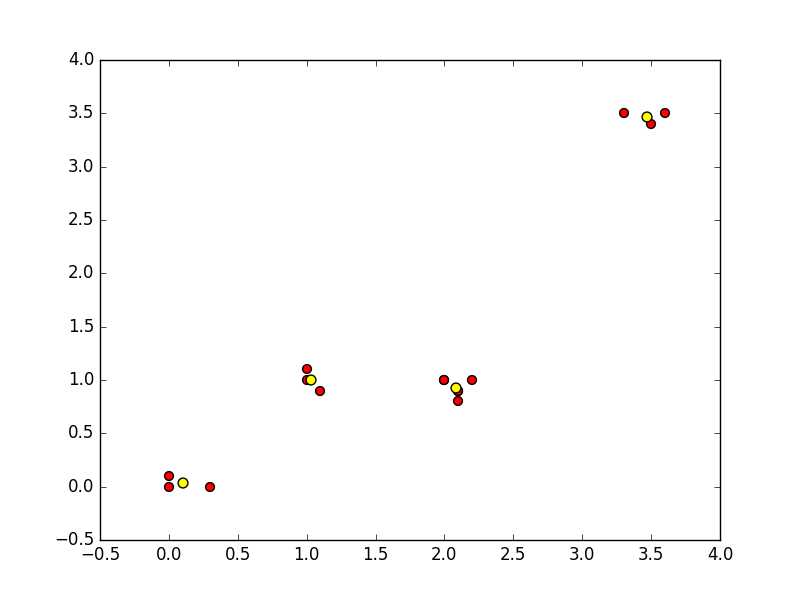
一种结果比较完美
尝试几次会出现以下不尽如人意的结果
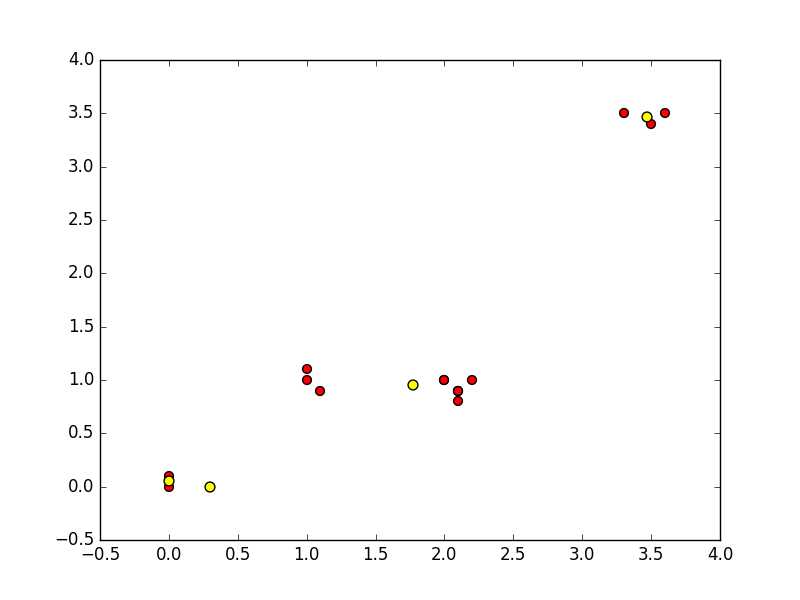
以上就是kmeans的具体实现方法,但这个方法并不尽人意,多次执行会发现聚类得到的点并不稳定,也不是每次都能得到我们想要的最佳结果,这是因为这个算法只能达到局部最优,不能保证全局最优,而这个原因就在于我们不能保证我们出是选取到的点是最佳的点。当然也是有改进方法的,我会继续更新下一节二分 k-均值算法
标签:归一化 学习 within [1] std rand center 技术 from
原文地址:http://www.cnblogs.com/greadlovejm/p/6074675.html