标签:oop stack rgb str crt 曲线 comm and pmi
本节介绍OpenGL中绘制直线、圆、椭圆,多边形的算法原理。
(1)绘制任意方向(任意斜率)的直线:
1)中点画线法:
中点画线法的算法原理不做介绍,但这里用到最基本的画0<=k<=1的中点画线法实现任意斜率k直线的绘制。
1)当A点x坐标值大于B点坐标值时,即A点在B点的右侧时,交换A、B点的坐标。保证A点在B的左侧。 2)考虑特殊情况,当直线AB的斜率不存在时,做近似处理,设置斜率为-(y0-y1)*100,即近似无穷大。 3)当斜率m满足0<=m<=1时,按书本上的中点画线算法进行处理。 4)当m>1时和m<0时,以y为步进选择对象,计算x基于y的斜率,再重复中点画线的过程。
代码如下:
1 #include<GL/glut.h> 2 #pragma comment(linker,"/subsystem:\"windows\" /entry:\"mainCRTStartup\"") 3 4 void myInit(){ 5 glMatrixMode(GL_MODELVIEW); 6 glLoadIdentity(); 7 gluOrtho2D(0.0, 480, 0.0, 480); 8 } 9 void Drawpixel(int x, int y){ 10 glPointSize(1.0); 11 glColor3f(1.0f, 0.0f, 0.0f);//设置颜色为红色 12 glVertex2i((int)(x), (int)(y)); 13 } 14 void MidpointLine(int x0, int y0, int x1, int y1) 15 { 16 int a, b, d1, d2, d, x, y; float m; 17 if (x1<x0){ 18 d = x0, x0 = x1, x1 = d; 19 d = y0, y0 = y1, y1 = d; 20 } 21 a = y0 - y1, b = x1 - x0; 22 if (b == 0) 23 m = -1 * a * 100; 24 else 25 m = (float)a / (x0 - x1); x = x0, y = y0; 26 Drawpixel(x, y); 27 if (m >= 0 && m <= 1){ 28 d = 2 * a + b; d1 = 2 * a, d2 = 2 * (a + b); 29 while (x<x1){ 30 if (d <= 0){ 31 x++, y++, d += d2; 32 } 33 else{ 34 x++, d += d1; 35 } 36 Drawpixel(x, y); 37 } 38 } 39 else if (m <= 0 && m >= -1){ 40 d = 2 * a - b; d1 = 2 * a - 2 * b, d2 = 2 * a; 41 while (x<x1){ 42 if (d>0){ x++, y--, d += d1; } 43 else{ 44 x++, d += d2; 45 } 46 Drawpixel(x, y); 47 } 48 } 49 else if (m>1){ 50 d = a + 2 * b; d1 = 2 * (a + b), d2 = 2 * b; 51 while (y<y1){ 52 if (d>0){ 53 x++, y++, d += d1; 54 } 55 else{ 56 y++, d += d2; 57 } 58 Drawpixel(x, y); 59 } 60 } 61 else{ 62 d = a - 2 * b; d1 = -2 * b, d2 = 2 * (a - b); 63 while (y>y1){ 64 if (d <= 0){ 65 x++, y--, d += d2; 66 } 67 else{ 68 y--, d += d1; 69 } 70 Drawpixel(x, y); 71 } 72 } 73 } 74 void myDisplay(){ 75 glClearColor(0, 0, 0, 0); 76 glClear(GL_COLOR_BUFFER_BIT); 77 glBegin(GL_POINTS); 78 MidpointLine(100, 100, 400, 400); 79 MidpointLine(400, 100, 100, 400); 80 glEnd(); 81 glFlush(); 82 } 83 int main(int argc, char **argv) 84 { 85 glutInit(&argc, argv); 86 glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB); 87 glutInitWindowSize(480, 480); 88 glutInitWindowPosition(200, 200); 89 glutCreateWindow("中点画线法"); 90 myInit(); 91 glutDisplayFunc(myDisplay); 92 glutMainLoop(); 93 return 0; 94 }
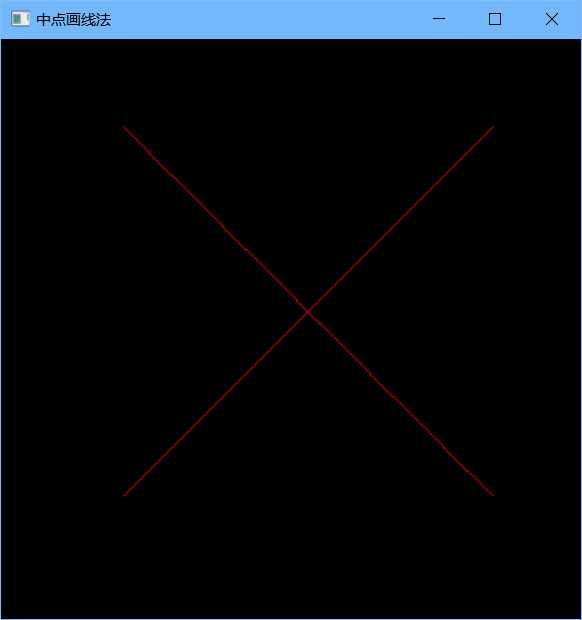
2)Breseham算法:
在这里依然不介绍Breseham的算法原理,但依然以它为基础。Breseham算法与中点算法一样也面临着只能处理0<k<1的情况,要扩展到任意斜率需要进行下述操作:
1)类似中点画线法,保证A(x0,y0)点在B(x1,y1)的左侧。 2)斜率为无穷大时单独画线; 3)其余情况分为4种情况: 一、斜率大于0小于1,按书本上的算法进行画线; 二、斜率大于1则交换横纵坐标; 三、斜率大于-1小于1的情况可先以y=y0作B点的对称点B‘,将AB’(此时斜率转化到情况二)画出之后,转化增量到相反的方向,画出直线AB; 四、当斜率小于-1时,先交换横纵坐标值转化为情况三,再利用情况三的算法转化为情况二进行画线。 总结:由于用的是转化法,无论斜率属于那种情况,计算增量的方式都转化到情况一上计算,因此我在这里将情况一抽象为一个函数,仅仅在画点时仅对不同情况做相应的坐标变换。
代码如下:
1 #include<GL/glut.h> 2 #pragma comment(linker,"/subsystem:\"windows\" /entry:\"mainCRTStartup\"") 3 4 void myInit(){ 5 glMatrixMode(GL_MODELVIEW); 6 glLoadIdentity(); 7 gluOrtho2D(0.0, 480, 0.0, 480); 8 } 9 void Drawpixel(int x, int y){ 10 glPointSize(1.0); 11 glColor3f(1.0f, 0.0f, 0.0f);//设置颜色为红色 12 glVertex2i((int)(x), (int)(y)); 13 } 14 void drawOrdinayLine(int x0, int y0, int x1, int y1, int flag){ 15 int i; 16 int x, y, dx, dy, e; 17 dx = x1 - x0; 18 dy = y1 - y0; 19 e = -dx; 20 x = x0; y = y0; 21 for (i = 0; i <= dx; i++){ 22 switch (flag){ 23 case 0: Drawpixel(x, y); break; 24 case 1: Drawpixel(x, 2 * y0 - y); break;//增量为(y-y0)则,实际增量应取相反方向为y0-(y-y0)=2y0-y 25 case 2: Drawpixel(y, x); break;//这里也要交换 26 case 3: Drawpixel(2 * y0 - y, x); break; 27 } 28 x++; 29 e = e + 2 * dy; 30 if (e >= 0){ 31 y++; 32 e = e - 2 * dx; 33 } 34 } 35 } 36 void BresenhamLine(int x0, int y0, int x1, int y1){ 37 int d; 38 int i; 39 if (x0>x1){ 40 d = x0, x0 = x1, x1 = d; 41 d = y0, y0 = y1, y1 = d; 42 } 43 if (x0 == x1){ 44 if (y0>y1){//保证y0<y1; 45 d = y0, y0 = y1, y1 = d; 46 } 47 for (i = y0; i< y1; i++){ 48 Drawpixel(x0, i); 49 } 50 return; 51 } 52 float k = (1.0*(y1 - y0)) / (x1 - x0); 53 if (0 <= k&&k <= 1){ //直接画 54 drawOrdinayLine(x0, y0, x1, y1, 0); 55 } 56 else if (-1 <= k&&k<0){//以y=y0作B点的对称点 57 drawOrdinayLine(x0, y0, x1, y1 + 2 * (y0 - y1), 1); 58 } 59 else if (k>1){//交换x,y的坐标值。 60 drawOrdinayLine(y0, x0, y1, x1, 2); 61 } 62 else if (k<-1){ 63 //交换x0和y0,x1和y1; 64 d = x0; x0 = y0; y0 = d; 65 d = x1; x1 = y1; y1 = d; 66 //交换两个点 67 d = x0, x0 = x1, x1 = d; 68 d = y0, y0 = y1, y1 = d; 69 drawOrdinayLine(x0, y0, x1, y1 + 2 * (y0 - y1), 3); 70 } 71 } 72 void myDisplay(){ 73 glClearColor(0, 0, 0, 0); 74 glClear(GL_COLOR_BUFFER_BIT); 75 glBegin(GL_POINTS); 76 int i; 77 BresenhamLine(200, 100, 300, 150); 78 BresenhamLine(200, 100, 300, 450); 79 BresenhamLine(125, 125, 400, 400); 80 BresenhamLine(125, 125, 75, 175); 81 glEnd(); 82 glFlush(); 83 } 84 int main(int argc, char **argv) 85 { 86 glutInit(&argc, argv); 87 glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB); 88 glutInitWindowSize(480, 480); 89 glutInitWindowPosition(200, 200); 90 glutCreateWindow("中点画线法"); 91 myInit(); 92 glutDisplayFunc(myDisplay); 93 glutMainLoop(); 94 return 0; 95 }
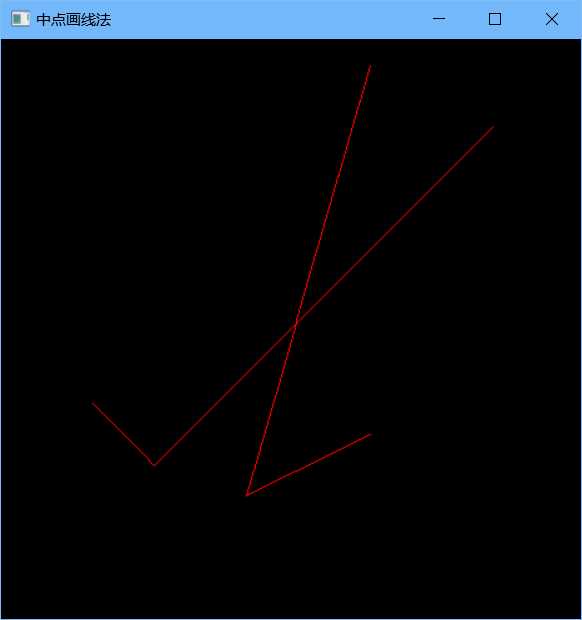
(2)绘制圆和椭圆:
中点画线法利用直线方程,画圆和椭圆利用的是椭圆和圆的方程。
1)中点画圆法:
标准中点画圆算法只能实现八分之一的圆弧,这里利用椭圆的点的对称性,每画一个点就对称的画出其他七段圆弧上的点。最后每个点均加上一个平移量,即圆的中点坐标,实现任意指定圆心坐标。
2)中点画椭圆法:
1)先画椭圆上顶点,然后以上顶点为基础运用椭圆的坐标方程式和中点画线法计算步进值。 2)从上顶点开始,每两个像素点组成一组画一条直线,一个像素点可同时当开始点和结束点。 3)利用椭圆的轴对称性对称的画出其它三条线。任意坐标的指定利用像素点的平移操作来进行。
代码如下:(圆和椭圆)
1 #include <GL/glut.h> 2 #include <math.h> 3 #pragma comment(linker,"/subsystem:\"windows\" /entry:\"mainCRTStartup\"") 4 5 void Init() 6 { 7 glClearColor(0,0,0,0); 8 glMatrixMode(GL_MODELVIEW); 9 glLoadIdentity(); 10 gluOrtho2D(-400,400,-400,400); 11 } 12 void CirclePoint(int x0,int y0,int x,int y){ 13 //每画一个点对称的画出八个点,并按照中点坐标平移相同单位 14 glVertex2d(x + x0, y + y0); 15 glVertex2d(x + x0, -y + y0); 16 glVertex2d(-x + x0, -y + y0); 17 glVertex2d(-x + x0, y + y0); 18 glVertex2d(y + x0, x + y0); 19 glVertex2d(-y + x0, x + y0); 20 glVertex2d(y + x0, -x + y0); 21 glVertex2d(-y + x0, -x + y0); 22 } 23 void MidPointCircle(int x0,int y0,int r){//圆点和半径 24 //画右上方1/8的圆 25 int x, y; 26 float d; 27 x = 0; y = r; 28 d = 1.25; 29 CirclePoint(x0, y0,x,y); 30 while (x <= y){ 31 if (d < 0) 32 d += 2 * x + 3; 33 else{ 34 d += 2 * (x - y) + 5; 35 y--; 36 } 37 x++; 38 CirclePoint(x0, y0, x, y); 39 } 40 } 41 42 void Drawpixel(int x, int y){ 43 glPointSize(1.0); 44 glColor3f(1.0f, 0.0f, 0.0f);//设置颜色为红色 45 glVertex2i((int)(x), (int)(y)); 46 } 47 void drawLine(int x0,int y0,int x1,int y1){ 48 int a, b, d1, d2, d, x, y; float m; 49 if (x1<x0){ 50 d = x0, x0 = x1, x1 = d; 51 d = y0, y0 = y1, y1 = d; 52 } 53 a = y0 - y1, b = x1 - x0; 54 if (b == 0) 55 m = -1 * a * 100; 56 else 57 m = (float)a / (x0 - x1); x = x0, y = y0; 58 Drawpixel(x, y); 59 if (m >= 0 && m <= 1){ 60 d = 2 * a + b; d1 = 2 * a, d2 = 2 * (a + b); 61 while (x<x1){ 62 if (d <= 0){ 63 x++, y++, d += d2; 64 } 65 else{ 66 x++, d += d1; 67 } 68 Drawpixel(x, y); 69 } 70 } 71 else if (m <= 0 && m >= -1){ 72 d = 2 * a - b; d1 = 2 * a - 2 * b, d2 = 2 * a; 73 while (x<x1){ 74 if (d>0){ x++, y--, d += d1; } 75 else{ 76 x++, d += d2; 77 } 78 Drawpixel(x, y); 79 } 80 } 81 else if (m>1){ 82 d = a + 2 * b; d1 = 2 * (a + b), d2 = 2 * b; 83 while (y<y1){ 84 if (d>0){ 85 x++, y++, d += d1; 86 } 87 else{ 88 y++, d += d2; 89 } 90 Drawpixel(x, y); 91 } 92 } 93 else{ 94 d = a - 2 * b; d1 = -2 * b, d2 = 2 * (a - b); 95 while (y>y1){ 96 if (d <= 0){ 97 x++, y--, d += d2; 98 } 99 else{ 100 y--, d += d1; 101 } 102 Drawpixel(x, y); 103 } 104 } 105 } 106 void drawOval(int x0,int y0,int a, int b){ 107 int x, y; 108 int xx, yy; 109 double d1, d2; 110 x = 0; y = b; 111 d1 = b*b + a*a*(-b + 0.25); 112 drawLine(x0 + x, y0 + y, x0+ x, y0 + y); 113 drawLine(x0 - x, y0-y, x0 - x, y0-y); 114 drawLine(x0 + x, y0-y, x0 + x, y0-y); 115 drawLine(x0 - x, y0+y, x0 - x, y0+y); 116 xx = x; yy = y; 117 while (b*b*(x + 1)<a*a*(y - 0.5)) 118 { 119 if (d1<0) 120 { 121 d1 += b*b*(2 * x + 3); 122 x++; 123 } 124 else 125 { 126 d1 += (b*b*(2 * x + 3) + a*a*(-2 * y + 2)); 127 x++; y--; 128 } 129 drawLine(x0 + xx, y0+yy, x0 + x, y0+y); 130 drawLine(x0 - xx, y0-yy, x0 - x, y0-y); 131 drawLine(x0 + xx, y0-yy, x0 + x, y0-y); 132 drawLine(x0 - xx, y0+yy, x0 - x, y0+y); 133 xx = x; yy = y; 134 } 135 d2 = sqrt(b*(x + 0.5)) + sqrt(a*(y - 1)) - sqrt(a*b); 136 while (y>0) 137 { 138 if (d2<0) 139 { 140 d2 += b*b*(2 * x + 2) + a*a*(-2 * y + 3); 141 x++; y--; 142 } 143 else 144 { 145 d2 += a*a*(-2 * y + 3); 146 y--; 147 } 148 drawLine(x0 + xx, y0+yy, x0 + x, y0+y); 149 drawLine(x0 - xx, y0-yy, x0 - x, y0-y); 150 drawLine(x0 + xx, y0-yy, x0 + x, y0-y); 151 drawLine(x0 - xx, y0+yy, x0 - x, y0+y); 152 xx = x; yy = y; 153 } 154 } 155 void display(){ 156 glClear(GL_COLOR_BUFFER_BIT); 157 glColor3f(1.0,1.0,0); 158 glBegin(GL_POINTS); 159 MidPointCircle(0, 50, 100); 160 MidPointCircle(0, -50, 100); 161 MidPointCircle(50, 0, 100); 162 MidPointCircle(-50, 0, 100); 163 //drawOval(100,0,200,100); 164 //drawOval(-100, 0, 200, 100); 165 //drawOval(0, 100, 200, 100); 166 //drawOval(0, -100, 200, 100); 167 glEnd(); 168 glFlush(); 169 } 170 int main(int argc, char * argv[]) 171 { 172 glutInit(&argc, argv); 173 glutInitDisplayMode(GLUT_RGB | GLUT_SINGLE); 174 glutInitWindowPosition(300, 100); 175 glutInitWindowSize(400, 400); 176 glutCreateWindow("椭圆与圆的绘制"); 177 Init(); 178 glutDisplayFunc(display); 179 glutMainLoop(); 180 return 0; 181 }
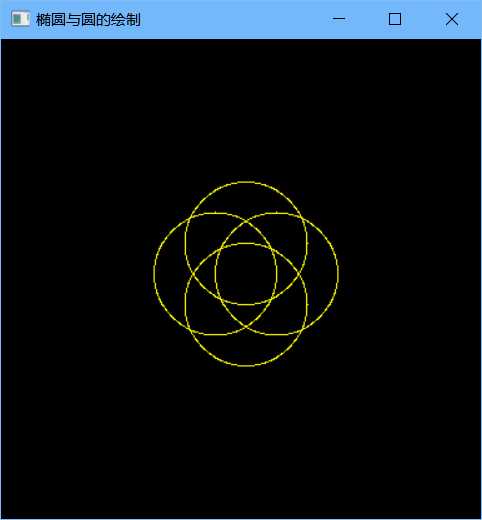
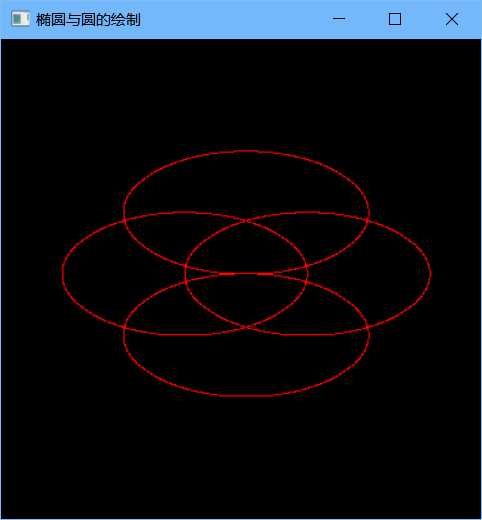
(3)绘制多边形:
1)多边形的扫描转化:
待扫描多边形的坐标如下,为了能够在窗体上观察清楚,这里我放大40倍。
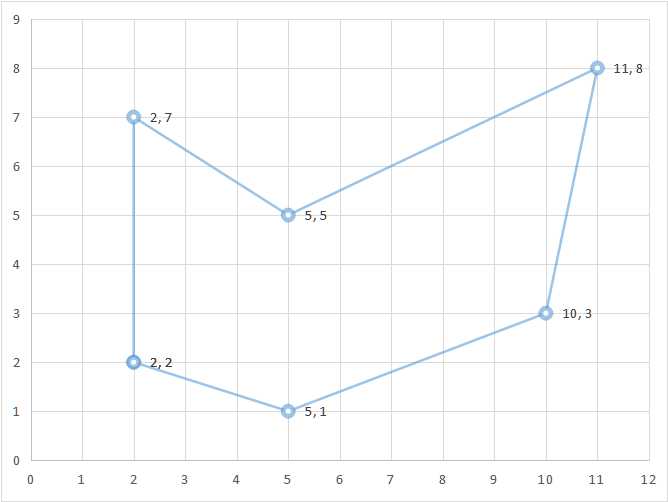
扫描线算法实现绘制填充多边形需要建立两张表:新边表(New Edge Table,NET)和 活动边表(Active Edge Table,AET);
新边表:记录多边形除水平边外的所有的边,记录在没条扫描线的表中,记录的格式为:
x_cross:当前扫描线与边的交点坐标;dx:从当前扫描线到下一条扫描线间x的增量((x2-x1)/(y2-y1));ymax:该边所交的最高扫描线。
建立的新边表如下:
格式: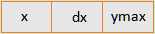
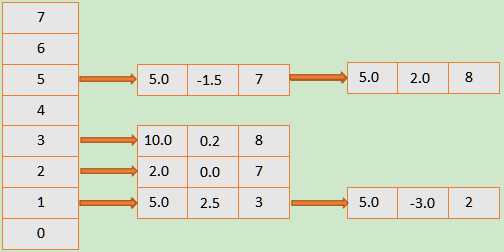
建立的活性边表如下:
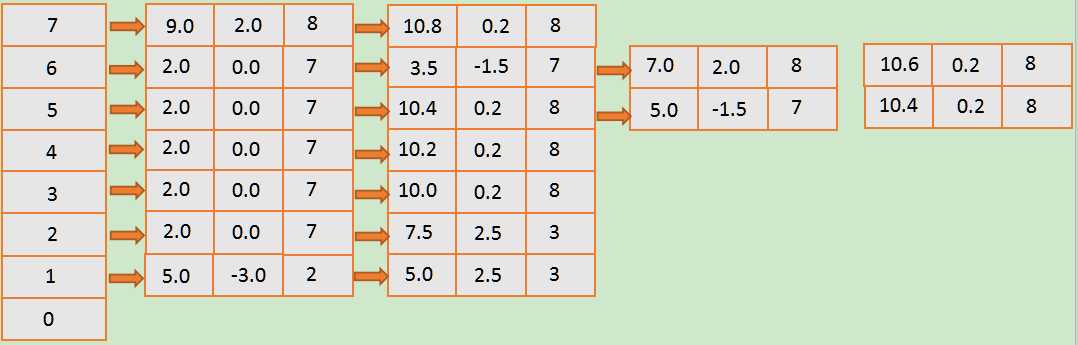
代码如下:
1 #include <GL/glut.h> 2 #include <stdio.h> 3 //待填充多边形的点的个数或边的个数 4 static int n; 5 //待填充多边形的顶点最大纵坐标值 6 static int max_y; 7 static int min_y; 8 struct POINT{ 9 int x;//多边形顶点横坐标 10 int y;//多边形顶点纵坐标 11 }; 12 typedef struct POINT Point; 13 struct EDGE{ 14 struct POINT *point[2];//存指向一条直线的两个点的指针 15 float k;//用来表示直线的斜率k=(x2-x1)/(y2-y1) 16 int flag;//用来标识一条边是否有效,当直线水平时此边无效,flag置为0。否则flag置为1。 17 }; 18 typedef struct EDGE Edge; 19 //组成边表和活性边表的结点 20 struct SHEETNODE{ 21 float x_cross;//扫描线与边交点的x坐标值 22 float dx;//dx从当前扫描线到下一条扫描线间x的增量((x2-x1)/(y2-y1)); 23 int y_max;//与当前扫描线相交的边的最大纵坐标y 24 struct SHEETNODE *next; 25 }; 26 typedef struct SHEETNODE SheetNode; 27 typedef struct SHEETNODE *Sheet; 28 Point *InitPoint(){ 29 n = 6;//六个点 30 Point *pNumGroup = malloc(n*sizeof(struct POINT)); 31 pNumGroup[0].x = 2; pNumGroup[0].y = 2; 32 pNumGroup[1].x = 5; pNumGroup[1].y = 1; 33 pNumGroup[2].x = 10; pNumGroup[2].y = 3; 34 pNumGroup[3].x =11; pNumGroup[3].y = 8; 35 pNumGroup[4].x = 5; pNumGroup[4].y = 5; 36 pNumGroup[5].x = 2; pNumGroup[5].y =7; 37 return pNumGroup; 38 } 39 void printPoints(Point *p){ 40 int i; 41 for (i = 0; i < n; i++){ 42 printf("第%d个顶点:x=%2d,y=%2d\n", i + 1, p[i].x, p[i].y); 43 } 44 } 45 Edge *InitEdge(Point *p){ 46 Edge *eNumGroup = malloc(n*sizeof(struct EDGE)); 47 int i; 48 for (i = 0; i < n; i++){ 49 eNumGroup[i].point[0] = &p[i]; 50 if (i != n - 1)//当当前边不是最后一条边时 51 eNumGroup[i].point[1] = &p[i + 1]; 52 else//当当前边是最后一条边时 53 eNumGroup[i].point[1] = &p[0]; 54 } 55 //初始化EDGE中的k和flag 56 for (i = 0; i < n; i++){ 57 //如果两个点的横坐标相同,代表斜率不存在,设为flag=1,边有效k=1 58 if (eNumGroup[i].point[0]->x == eNumGroup[i].point[1]->x) 59 { 60 eNumGroup[i].flag = 1; eNumGroup[i].k = 0; 61 } 62 //如果两个点的纵坐标相同,代表斜率为1,属于无效边。flag=0; 63 else if (eNumGroup[i].point[0]->y == eNumGroup[i].point[1]->y) 64 eNumGroup[i].flag = 0; 65 else{ 66 eNumGroup[i].flag = 1; 67 eNumGroup[i].k = 1.0* (eNumGroup[i].point[0]->x - eNumGroup[i].point[1]->x) / (eNumGroup[i].point[0]->y - eNumGroup[i].point[1]->y); 68 } 69 } 70 return eNumGroup; 71 } 72 int Min(int a, int b){ 73 return a > b ? b : a; 74 } 75 int Max(int a, int b){ 76 return a>b ? a : b; 77 } 78 void printEdge(Edge *edge){ 79 int i; 80 for (i = 0; i < n; i++){ 81 if (edge[i].flag == 1) 82 printf("边%d有效,斜率为%2.1f\n", i + 1, edge[i].k); 83 } 84 } 85 //按x的递增顺序将结点插入边表 86 void InsertIntoSheet(SheetNode *tempNode, Sheet sheet){ 87 SheetNode *ptr = sheet; 88 while (ptr->next != NULL){ 89 if (tempNode->x_cross <= ptr->next->x_cross){ 90 tempNode->next = ptr->next; 91 ptr->next = tempNode; 92 return; 93 } 94 else{ 95 ptr = ptr->next; 96 } 97 } 98 ptr->next = tempNode; 99 } 100 Sheet InitNewEdgeSheet(Edge *e){ 101 int i; int tempMax, tempMin; 102 max_y = e[0].point[0]->y; 103 min_y = e[0].point[0]->y; 104 for (i = 0; i < n; i++){ 105 tempMax = Max(e[i].point[0]->y, e[i].point[1]->y); 106 tempMin = Min(e[i].point[0]->y, e[i].point[1]->y); 107 if (max_y < tempMax) 108 max_y = tempMax; 109 if (min_y>tempMin){ 110 min_y = tempMin; 111 } 112 } 113 //新边表 114 int j; 115 //标记边是否被插入新边表的标志数组 116 int *EdgeIntoSheetFlag = malloc(n*sizeof(int)); 117 for (i = 0; i < n; i++){ 118 EdgeIntoSheetFlag[i] = 0; 119 } 120 Sheet s = malloc(max_y*sizeof(struct SHEETNODE)); 121 for (i = 0; i <max_y; i++){ 122 s[i].next = NULL; 123 } 124 for (i = 0; i <max_y; i++){ 125 //讨论y=i这条扫描线与每条边的相交情况 126 for (j = 0; j < n; j++){ 127 //如果这条边已经用过了,忽略这条边 128 if (EdgeIntoSheetFlag[j] == 1) 129 continue; 130 //如果扫描线与边相交==>y=i在当前边的最大y值和最小y值之间 131 if ((i <= e[j].point[0]->y&&i >= e[j].point[1]->y) || (i <= e[j].point[1]->y) && (i >= e[j].point[0]->y)){ 132 EdgeIntoSheetFlag[j] = 1; 133 SheetNode *tempNode = malloc(sizeof(struct SHEETNODE)); 134 tempNode->dx = e[j].k; 135 tempNode->y_max = Max(e[j].point[0]->y, e[j].point[1]->y); 136 //取一条直线的任意端点,这里使用第一个点。交点的横坐标为x=k(i-y0)+y0 137 tempNode->x_cross = e[j].k*(i - e[j].point[0]->y) + e[j].point[0]->x; 138 tempNode->next = NULL; 139 //printf("插入 %.1f,%.1f,%d\n", tempNode->dx, tempNode->x_cross, tempNode->y_max); 140 InsertIntoSheet(tempNode, &s[i]); 141 } 142 } 143 } 144 return s; 145 } 146 void printSheet(Sheet sheet){ 147 int i; 148 for (i = 0; i <max_y; i++){ 149 SheetNode *ptr = &sheet[i]; 150 while (ptr->next != NULL){ 151 printf("dx=%.1f x_cross=%.1f y_max=%d\n", ptr->next->dx, ptr->next->x_cross, ptr->next->y_max); 152 ptr = ptr->next; 153 } 154 } 155 } 156 Sheet InitDynamicEdgeSheet(Sheet sheet){ 157 int i; 158 int j; 159 Sheet s_dynamic = malloc(max_y*sizeof(struct SHEETNODE)); 160 for (i = 0; i <max_y; i++){ 161 s_dynamic[i].next = NULL; 162 } 163 SheetNode *tempNode; 164 SheetNode *ptrNode; 165 for (i = 0; i <max_y; i++){ 166 SheetNode *ptr = &sheet[i]; 167 while (ptr->next != NULL){ 168 tempNode = malloc(sizeof(struct SHEETNODE)); 169 tempNode->next = NULL; 170 tempNode->dx = ptr->next->dx; 171 tempNode->x_cross = ptr->next->x_cross; 172 tempNode->y_max = ptr->next->y_max; 173 //printf("插入 %.1f,%.1f,%d\n", tempNode->dx, tempNode->x_cross, tempNode->y_max); 174 InsertIntoSheet(tempNode, &s_dynamic[i]); 175 if (tempNode->y_max>i){ 176 for (j = i + 1; j < tempNode->y_max; j++){ 177 ptrNode = malloc(sizeof(struct SHEETNODE)); 178 ptrNode->next = NULL; 179 ptrNode->dx = tempNode->dx; 180 ptrNode->y_max = tempNode->y_max; 181 //printf("%f\n",tempNode->dx); 182 ptrNode->x_cross = tempNode->x_cross + (j - i)*tempNode->dx; 183 //printf("插入 %.1f,%.1f,%d\n", ptrNode->dx, ptrNode->x_cross, ptrNode->y_max); 184 InsertIntoSheet(ptrNode, &s_dynamic[j]); 185 } 186 } 187 ptr = ptr->next; 188 } 189 } 190 return s_dynamic; 191 } 192 void displayLine(Point A, Point B){ 193 glColor3f(1.0, 0.0, 0); 194 glBegin(GL_LINES); 195 //printf("A.x=%d A.y=%d",A.x,A.y); 196 //printf("B.x=%d B.y=%d", B.x, B.y); 197 //printf("\n"); 198 glVertex2i(A.x, A.y); 199 glVertex2i(B.x, B.y); 200 glEnd(); 201 } 202 void paint(Sheet sheet){ 203 int i; int minNum; int j; 204 SheetNode *ptrNode = NULL; 205 SheetNode *A_Node = NULL; 206 SheetNode *B_Node = NULL; 207 for (i = 0; i < max_y; i++){ 208 ptrNode = &sheet[i]; 209 while (ptrNode->next != NULL){ 210 //结点总是成对出现 211 A_Node = ptrNode->next; 212 B_Node = ptrNode->next->next; 213 Point A, B; 214 A.y = i; B.y = i; 215 A.x = A_Node->x_cross; 216 B.x = B_Node->x_cross; 217 displayLine(A, B); 218 ptrNode = ptrNode->next->next; 219 } 220 } 221 } 222 Sheet ProcessBegin(){ 223 //1.按顺序将多边形顶点输入数组 224 Point *p = NULL; 225 p = InitPoint(); 226 printf("1.输出多边形的所有顶点坐标:\n"); printPoints(p); 227 //2.依据顶点初始化此多边形的各个边 228 Edge *e = NULL; 229 e = InitEdge(p); 230 printf("2.打印待扫描多边形所有的边\n"); printEdge(e); 231 //3.初始化新边表 232 Sheet newSheet = NULL; 233 newSheet = InitNewEdgeSheet(e); 234 printf("3.打印新边表:\n"); printSheet(newSheet); 235 //4.初始化活性边表 236 Sheet dynamicSheet = NULL; 237 dynamicSheet = InitDynamicEdgeSheet(newSheet); 238 printf("4.打印活性边表:\n"); printSheet(dynamicSheet); 239 //进行多边形扫描转化 240 return dynamicSheet; 241 } 242 void Init(){ 243 glClearColor(0, 0, 0, 0); 244 glMatrixMode(GL_PROJECTION); 245 glLoadIdentity(); 246 //定义裁剪区域 247 gluOrtho2D(0, 500, 0, 400); 248 } 249 250 void display(void){ 251 glClear(GL_COLOR_BUFFER_BIT); 252 glColor3d(1.0, 0, 0); 253 Sheet tempSheet = ProcessBegin(); 254 paint(tempSheet); 255 glFlush(); 256 } 257 int main(int argc, char *argv[]){ 258 glutInit(&argc, argv); 259 glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB); 260 glutInitWindowPosition(400, 200); 261 glutInitWindowSize(500, 400); 262 glutCreateWindow("扫描线画多边形"); 263 glutDisplayFunc(display); 264 Init(); 265 glutMainLoop(); 266 return 0; 267 }
控制台输出:
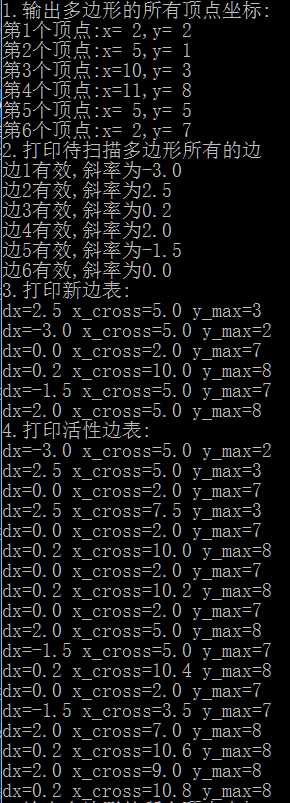
图形绘制:
由于这里图形太小所以多边形的扫描转化并不明显,因此我将每个坐标扩大40倍,通过修改代码中的initPoints()函数实现:
Point *InitPoint(){ n = 6;//六个点 Point *pNumGroup = malloc(n*sizeof(struct POINT)); pNumGroup[0].x = 4*20; pNumGroup[0].y = 4*20; pNumGroup[1].x = 4*50; pNumGroup[1].y = 4*10; pNumGroup[2].x = 4*100; pNumGroup[2].y = 4*30; pNumGroup[3].x = 4*110; pNumGroup[3].y = 4*80; pNumGroup[4].x = 4*50; pNumGroup[4].y = 4*50; pNumGroup[5].x = 4*20; pNumGroup[5].y = 4*70; return pNumGroup; }
效果如下:(由于活性边表太长无法显示全部)
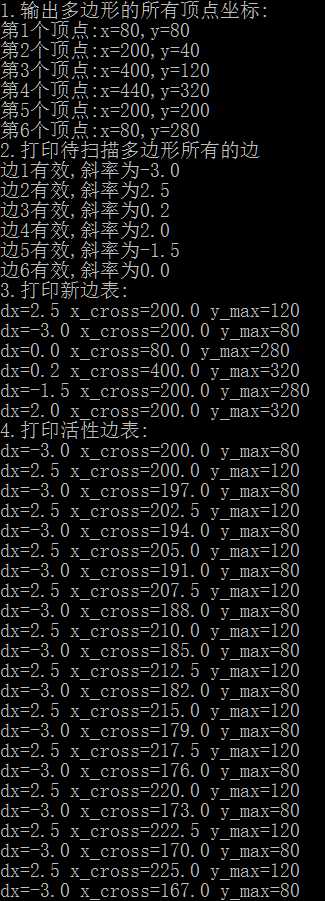
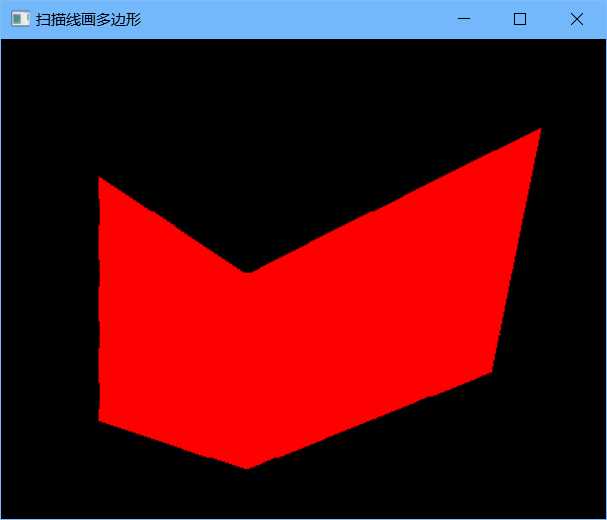
2)多边形的区域填充:
在多边形的扫描转化的测试中已经涉及到多边形的区域填充,不过那里由活性边表绘制直线得到,这里讨论的是已经表示成点阵形式的填充图形,是像素的集合。
区域的表示可采用内点或者边界点表示两种表示形式。在内点表示中,区域内的所有像素着同一颜色;在边界点表示中,区域的边界点着同一颜色。区域填充是指先将区域内的一点赋予指定的颜色,然后将该颜色扩展到整个区域的过程。
区域分为四连通和八连通两种。这里以八连通区域为例介绍区域的递归填充算法和扫描线算法。
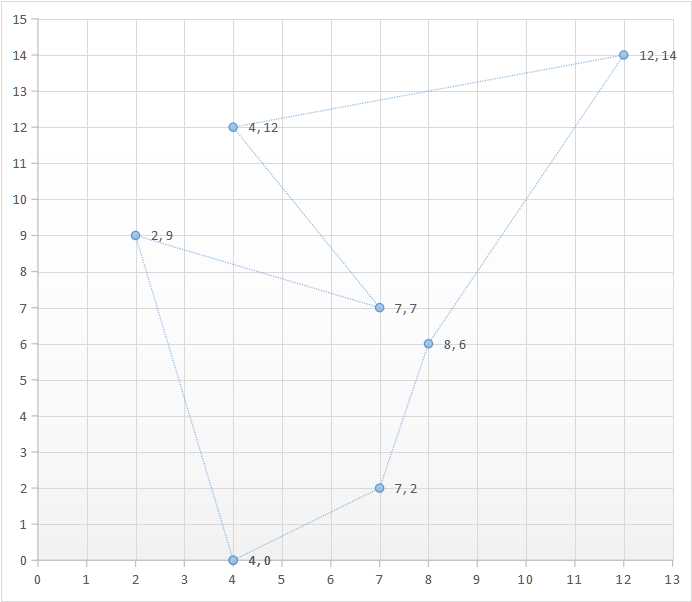
3.2.1区域填充的递归算法:
1 /* 2 ---------------------------------八连通多边形区域填充递归算法--------------------------------------------------- 3 1.初始化绘图区域的边界线的端点坐标(这里直线为例,不介绍曲线) 4 2.依据顶点初始化边界线 5 3.新建二维数组保存点阵的状态,数组值为1代表边界,0代表非边界 6 4.利用中点画线法计算各条边界线经过的像素,并将点阵中的对应坐标的值置为1,表示边界 7 上述过程意在完成图形的栅格化,并表示为点阵的形式,下面开始区域填充算法 8 5.根据点阵和递归填充算法将栅格化的图形画在显示窗体上 9 */ 10 //待填充多边形的点的个数或边的个数 11 #include <stdio.h> 12 #include <GL/glut.h> 13 14 static int n; 15 static int y_max; 16 static int x_max; 17 struct POINT{ 18 int x;//多边形顶点横坐标 19 int y;//多边形顶点纵坐标 20 }; 21 typedef struct POINT Point; 22 static Point seed;//种子坐标值 23 Point *InitPoint(){ 24 n = 7;//六个点 25 Point *pNumGroup = malloc(n*sizeof(struct POINT)); 26 pNumGroup[0].x = 4; pNumGroup[0].y = 0; 27 pNumGroup[1].x = 7; pNumGroup[1].y = 2; 28 pNumGroup[2].x = 8; pNumGroup[2].y = 6; 29 pNumGroup[3].x = 12;pNumGroup[3].y = 14; 30 pNumGroup[4].x = 4; pNumGroup[4].y = 12; 31 pNumGroup[5].x = 7; pNumGroup[5].y = 7; 32 pNumGroup[6].x = 2; pNumGroup[6].y = 9; 33 seed.x = 5;seed.y = 5; 34 return pNumGroup; 35 } 36 void setEdge(int x, int y, int **NumGroup){ 37 NumGroup[x][y] = 1; 38 //printf("NumGroup[%d][%d]=1",x,y); 39 } 40 void MidpointLine(int x0, int y0, int x1, int y1, int **NumGroup) 41 { 42 int a, b, d1, d2, d, x, y; float m; 43 if (x1<x0){ 44 d = x0, x0 = x1, x1 = d; 45 d = y0, y0 = y1, y1 = d; 46 } 47 a = y0 - y1, b = x1 - x0; 48 if (b == 0) 49 m = -1 * a * 100; 50 else 51 m = (float)a / (x0 - x1); x = x0, y = y0; 52 setEdge(x, y, NumGroup); 53 if (m >= 0 && m <= 1){ 54 d = 2 * a + b; d1 = 2 * a, d2 = 2 * (a + b); 55 while (x<x1){ 56 if (d <= 0){ 57 x++, y++, d += d2; 58 } 59 else{ 60 x++, d += d1; 61 } 62 setEdge(x, y, NumGroup); 63 } 64 } 65 else if (m <= 0 && m >= -1){ 66 d = 2 * a - b; d1 = 2 * a - 2 * b, d2 = 2 * a; 67 while (x<x1){ 68 if (d>0){ x++, y--, d += d1; } 69 else{ 70 x++, d += d2; 71 } 72 setEdge(x, y, NumGroup); 73 } 74 } 75 else if (m>1){ 76 d = a + 2 * b; d1 = 2 * (a + b), d2 = 2 * b; 77 while (y<y1){ 78 if (d>0){ 79 x++, y++, d += d1; 80 } 81 else{ 82 y++, d += d2; 83 } 84 setEdge(x, y, NumGroup); 85 } 86 } 87 else{ 88 d = a - 2 * b; d1 = -2 * b, d2 = 2 * (a - b); 89 while (y>y1){ 90 if (d <= 0){ 91 x++, y--, d += d2; 92 } 93 else{ 94 y--, d += d1; 95 } 96 setEdge(x, y, NumGroup); 97 } 98 } 99 } 100 //在视窗上将此矩阵输出 101 void printEdgeMatrix(int **NumGroupMaxtrx, int x_num, int y_num){ 102 int i; 103 int j; 104 for (i = 0; i < x_num; i++){ 105 for (j = 0; j < y_num; j++){ 106 //如果是边界点 107 if (NumGroupMaxtrx[i][j] == 1){ 108 glVertex2i(i, j); 109 } 110 } 111 112 } 113 } 114 int **InitPointMatrixByPoint(Point *p){ 115 int i; 116 y_max = p[0].x; 117 x_max = p[0].y; 118 for (i = 0; i < n;i++){ 119 if (p[i].x>x_max) 120 x_max = p[i].x; 121 if (p[i].y > y_max) 122 y_max =p[i].y; 123 } 124 y_max++; x_max++; 125 int **NumGroup_Matrix = malloc(x_max*sizeof(int *)); 126 for (i = 0; i < x_max;i++){ 127 NumGroup_Matrix[i] = malloc(y_max*sizeof(int)); 128 } 129 int j; 130 for (i = 0; i < x_max;i++){ 131 for (j = 0; j < y_max;j++){ 132 //取值有-1,0,1三种情况分别表示无效,内点和边界点 133 NumGroup_Matrix[i][j] = -1; 134 } 135 } 136 //printf("%d,%d",p[5].x,p[5].y); 137 for (i = 0; i < n; i++){ 138 if (i != n - 1) 139 MidpointLine(p[i].x, p[i].y, p[i + 1].x, p[i + 1].y,NumGroup_Matrix); 140 else 141 MidpointLine(p[i].x, p[i].y, p[0].x, p[0].y,NumGroup_Matrix); 142 } 143 //这句话用来测试边界表示多边形边界是否正确 144 //printEdgeMatrix(NumGroup_Matrix,x_max,y_max); 145 return NumGroup_Matrix; 146 } 147 void fixPaint(int **numGroup,int x,int y){ 148 if (x<0||y<0||x>=x_max||y>=y_max){ 149 return; 150 } 151 //如果当前点是无效点,说明其在区域内部 152 if (numGroup[x][y] == -1){ 153 glVertex2i(x,y); 154 numGroup[x][y] = 0; 155 fixPaint(numGroup, x, y + 1); 156 fixPaint(numGroup, x, y - 1); 157 fixPaint(numGroup, x+1, y); 158 fixPaint(numGroup, x-1, y); 159 fixPaint(numGroup, x + 1, y+1); 160 fixPaint(numGroup, x + 1, y-1); 161 fixPaint(numGroup, x - 1, y+1); 162 fixPaint(numGroup, x - 1, y-1); 163 } 164 else{ 165 return; 166 } 167 } 168 void ProcessExcute(){ 169 //1.初始化待填充区域的边界线段端点和种子坐标 170 Point *p=InitPoint(); 171 //2.栅格化边界线段端点表示的待填充区域到像素阵列数组里 172 int **numGroupMatrix = InitPointMatrixByPoint(p); 173 //3.用递归法处理八连通区域的方法将栅格化的像素矩阵表示的区域填充 174 fixPaint(numGroupMatrix,seed.x,seed.y); 175 } 176 void display(){ 177 glClear(GL_COLOR_BUFFER_BIT); 178 glColor3d(1.0, 0, 0); 179 glBegin(GL_POINTS); 180 ProcessExcute(); 181 glEnd(); 182 glFlush();; 183 } 184 //原画像素函数drawPixel改编而来 185 186 void Init(){ 187 glClearColor(0, 0, 0, 0); 188 glMatrixMode(GL_PROJECTION); 189 glLoadIdentity(); 190 //定义裁剪区域 191 gluOrtho2D(0, 500, 0, 400); 192 } 193 int main(int argc, char *argv[]){ 194 glutInit(&argc, argv); 195 glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB); 196 glutInitWindowPosition(400, 200); 197 glutInitWindowSize(500, 400); 198 glutCreateWindow("扫描线画多边形"); 199 Init(); 200 glutDisplayFunc(display); 201 glutMainLoop(); 202 return 0; 203 }
八连通区域处理区域填充时不可避免的要出现像素向原本不应该是区域内部的像素扩展,最终导致除边界像素外,所有的像素均被着色:
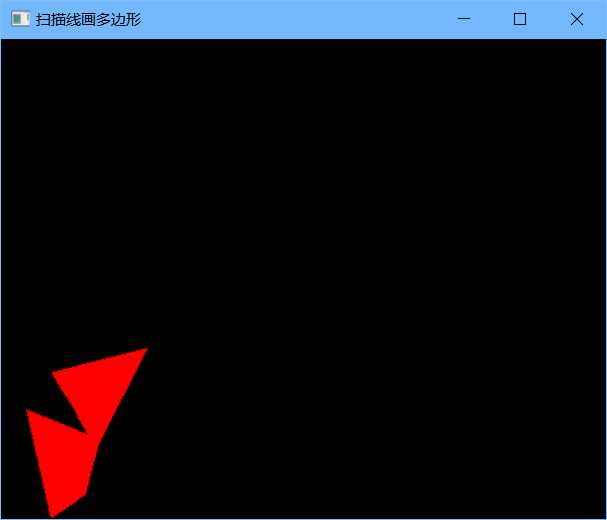
四连通区域不会出现这个问题:(将点的坐标均扩大10倍,将递归函数的八连通改为四连通):
Point *InitPoint(){ n = 7;//六个点 Point *pNumGroup = malloc(n*sizeof(struct POINT)); pNumGroup[0].x = 40; pNumGroup[0].y = 00; pNumGroup[1].x = 70; pNumGroup[1].y = 20; pNumGroup[2].x = 80; pNumGroup[2].y = 60; pNumGroup[3].x = 120; pNumGroup[3].y = 140; pNumGroup[4].x = 40; pNumGroup[4].y = 120; pNumGroup[5].x = 70; pNumGroup[5].y = 70; pNumGroup[6].x = 20; pNumGroup[6].y = 90; seed.x = 50; seed.y = 50; return pNumGroup; } void fixPaint(int **numGroup, int x, int y){ if (x<0 || y<0 || x>=x_max || y>=y_max){ return; } //如果当前点是无效点,说明其在区域内部 if (numGroup[x][y] == -1){ glVertex2i(x, y); numGroup[x][y] = 0; fixPaint(numGroup, x, y + 1); fixPaint(numGroup, x, y - 1); fixPaint(numGroup, x + 1, y); fixPaint(numGroup, x - 1, y); //fixPaint(numGroup, x + 1, y + 1); //fixPaint(numGroup, x + 1, y - 1); //fixPaint(numGroup, x - 1, y + 1); //fixPaint(numGroup, x - 1, y - 1); } else{ return; } }
解决方法:
这就要求八连通区域所有的直线的斜率都必须是0或者不存在,类似下题:
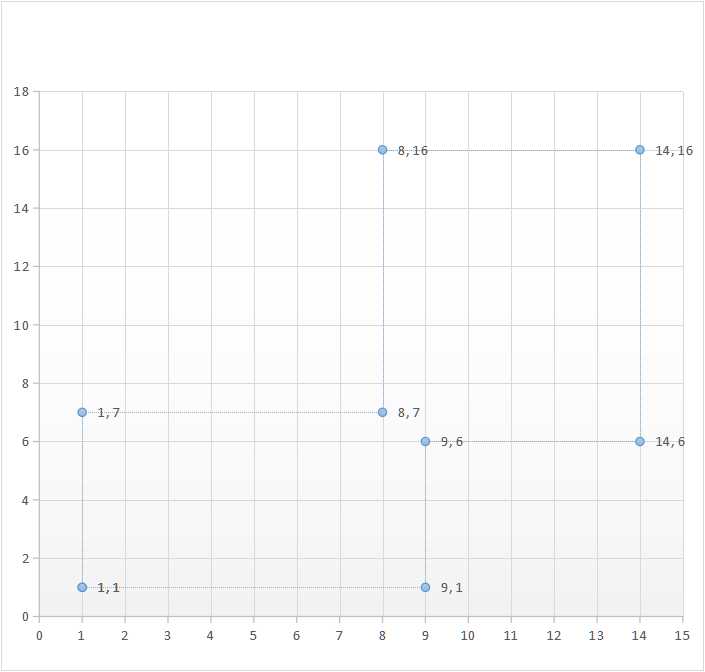
修改上述初始化点的代码为:(其余不变),并放大6倍后显示:(最大只能放大6倍,6倍以上时程序会提醒fixPaint递归函数处中断,原因不明)
Point *InitPoint(){ n = 8;//六个点 Point *pNumGroup = malloc(n*sizeof(struct POINT)); pNumGroup[0].x =6* 1; pNumGroup[0].y =6* 1; pNumGroup[1].x =6* 9; pNumGroup[1].y =6* 1; pNumGroup[2].x =6* 9; pNumGroup[2].y =6* 6; pNumGroup[3].x =6 *14; pNumGroup[3].y = 6 * 6; pNumGroup[4].x =6* 14; pNumGroup[4].y = 6*16; pNumGroup[5].x =6* 8; pNumGroup[5].y = 6*16; pNumGroup[6].x =6* 8; pNumGroup[6].y = 6*7; pNumGroup[7].x =6* 1; pNumGroup[7].y = 6*7; seed.x = 6*5; seed.y = 6*5; return pNumGroup; }
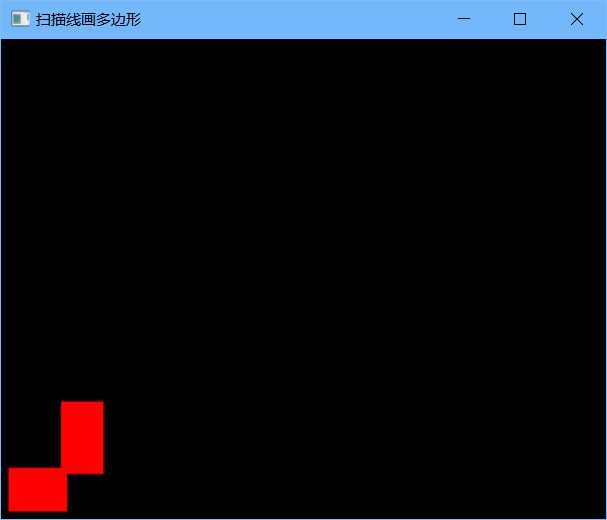
3.2.2区域填充的扫描线算法:
扫描线区域填充算法和递归八连通区域填充算法一样无法解决斜率不为0或无穷大时的情况,因此测试时边界线的斜率必须k=0或者k无穷大
扫描线区域填充算法的原理:
1)初始化,堆栈置空,将种子结点入栈; 2)出栈,若栈空则结束;否则取栈顶元素,以栈顶元素的纵坐标y为当前扫描线; 3)填充并确定种子所在区段。从种子出发沿当前扫描线向左右两个方向填充直到边界。分别标记区段左右两端的坐标为left和right; 4)确定新的种子点。在区间[left,right]中检查与当前扫描线y上下相邻的两条扫描线上的像素。若存在非边界,未填充的像素,则把每一区间最右像素作为种子点压入堆栈。 5)返回第二步,直至栈为空。
1 /* 2 ---------------------------------区域填充扫描线算法--------------------------------------------------- 3 1.初始化绘图区域的边界线的端点坐标(这里直线为例,不介绍曲线) 4 2.依据顶点初始化边界线 5 3.新建二维数组保存点阵的状态,数组值为1代表边界,0代表非边界 6 4.利用中点画线法计算各条边界线经过的像素,并将点阵中的对应坐标的值置为1,表示边界 7 上述过程意在完成图形的栅格化,并表示为点阵的形式,下面开始区域填充算法 8 5.根据点阵和扫描线算法将栅格化的图形画在显示窗体上 9 */ 10 #include <stdio.h> 11 #include <GL/glut.h> 12 13 //待填充多边形的点的个数或边的个数 14 static int n; 15 static int y_max; 16 static int x_max; 17 struct POINT{ 18 int x;//多边形顶点横坐标 19 int y;//多边形顶点纵坐标 20 }; 21 typedef struct POINT Point; 22 static Point seed;//种子坐标值 23 Point *InitPoint(){ 24 n = 8;//六个点 25 Point *pNumGroup = malloc(n*sizeof(struct POINT)); 26 pNumGroup[0].x = 1; pNumGroup[0].y = 1; 27 pNumGroup[1].x = 9; pNumGroup[1].y = 1; 28 pNumGroup[2].x = 9; pNumGroup[2].y = 6; 29 pNumGroup[3].x = 14; pNumGroup[3].y = 6; 30 pNumGroup[4].x = 14; pNumGroup[4].y = 16; 31 pNumGroup[5].x = 8; pNumGroup[5].y = 16; 32 pNumGroup[6].x = 8; pNumGroup[6].y = 7; 33 pNumGroup[7].x = 1; pNumGroup[7].y = 7; 34 seed.x = 5; seed.y = 5; 35 return pNumGroup; 36 } 37 //原画像素函数drawPixel改编而来 38 void setEdge(int x, int y, int **NumGroup){ 39 NumGroup[x][y] = 1; 40 } 41 void MidpointLine(int x0, int y0, int x1, int y1, int **NumGroup) 42 { 43 int a, b, d1, d2, d, x, y; float m; 44 if (x1<x0){ 45 d = x0, x0 = x1, x1 = d; 46 d = y0, y0 = y1, y1 = d; 47 } 48 a = y0 - y1, b = x1 - x0; 49 if (b == 0) 50 m = -1 * a * 100; 51 else 52 m = (float)a / (x0 - x1); x = x0, y = y0; 53 setEdge(x, y, NumGroup); 54 if (m >= 0 && m <= 1){ 55 d = 2 * a + b; d1 = 2 * a, d2 = 2 * (a + b); 56 while (x<x1){ 57 if (d <= 0){ 58 x++, y++, d += d2; 59 } 60 else{ 61 x++, d += d1; 62 } 63 setEdge(x, y, NumGroup); 64 } 65 } 66 else if (m <= 0 && m >= -1){ 67 d = 2 * a - b; d1 = 2 * a - 2 * b, d2 = 2 * a; 68 while (x<x1){ 69 if (d>0){ x++, y--, d += d1; } 70 else{ 71 x++, d += d2; 72 } 73 setEdge(x, y, NumGroup); 74 } 75 } 76 else if (m>1){ 77 d = a + 2 * b; d1 = 2 * (a + b), d2 = 2 * b; 78 while (y<y1){ 79 if (d>0){ 80 x++, y++, d += d1; 81 } 82 else{ 83 y++, d += d2; 84 } 85 setEdge(x, y, NumGroup); 86 } 87 } 88 else{ 89 d = a - 2 * b; d1 = -2 * b, d2 = 2 * (a - b); 90 while (y>y1){ 91 if (d <= 0){ 92 x++, y--, d += d2; 93 } 94 else{ 95 y--, d += d1; 96 } 97 setEdge(x, y, NumGroup); 98 } 99 } 100 } 101 //在视窗上将此矩阵输出 102 void printEdgeMatrix(int **NumGroupMaxtrx, int x_num, int y_num){ 103 int i; 104 int j; 105 for (i = 0; i < x_num; i++){ 106 for (j = 0; j < y_num; j++){ 107 //如果是边界点 108 if (NumGroupMaxtrx[i][j] == 1){ 109 glVertex2i(i, j); 110 } 111 } 112 113 } 114 } 115 int **InitPointMatrixByPoint(Point *p){ 116 int i; 117 y_max = p[0].x; 118 x_max = p[0].y; 119 for (i = 0; i < n; i++){ 120 if (p[i].x>x_max) 121 x_max = p[i].x; 122 if (p[i].y > y_max) 123 y_max = p[i].y; 124 } 125 y_max++; x_max++; 126 int **NumGroup_Matrix = malloc(x_max*sizeof(int *)); 127 for (i = 0; i < x_max; i++){ 128 NumGroup_Matrix[i] = malloc(y_max*sizeof(int)); 129 } 130 int j; 131 for (i = 0; i < x_max; i++){ 132 for (j = 0; j < y_max; j++){ 133 //取值有-1,0,1三种情况分别表示无效,内点和边界点 134 NumGroup_Matrix[i][j] = -1; 135 } 136 } 137 //printf("%d,%d",p[5].x,p[5].y); 138 for (i = 0; i < n; i++){ 139 if (i != n - 1) 140 MidpointLine(p[i].x, p[i].y, p[i + 1].x, p[i + 1].y, NumGroup_Matrix); 141 else 142 MidpointLine(p[i].x, p[i].y, p[0].x, p[0].y, NumGroup_Matrix); 143 } 144 //这句话用来测试边界表示多边形边界是否正确 145 //printEdgeMatrix(NumGroup_Matrix,x_max,y_max); 146 return NumGroup_Matrix; 147 } 148 struct STACKNODE{ 149 Point point; 150 struct STACKNODE *next; 151 }; 152 typedef struct STACKNODE *PtrToNode; 153 typedef struct STACKNODE *Stack; 154 Stack createStack(){ 155 Stack stack = malloc(sizeof(struct STACKNODE)); 156 stack->next = NULL; 157 return stack; 158 } 159 void *Push(Stack stack,Point point){ 160 PtrToNode tempNode = malloc(sizeof(struct STACKNODE)); 161 tempNode->point.x = point.x; 162 tempNode->point.y = point.y; 163 tempNode->next = stack->next; 164 stack->next = tempNode; 165 } 166 Point *PopAndTop(Stack stack){ 167 PtrToNode ptr = stack->next; 168 stack->next = stack->next->next; 169 return &ptr->point; 170 } 171 int IsNull(Stack s){ 172 if (s->next == NULL) 173 return 1; 174 else 175 return 0; 176 } 177 void scanLineFixArea(int **numGroupMatrix){ 178 Stack s = createStack(); 179 Push(s,seed); 180 Point *tempPoint; 181 Point left, right; 182 int i; 183 while (!IsNull(s)){ 184 tempPoint = PopAndTop(s); 185 glVertex2i(tempPoint->x, tempPoint->y); numGroupMatrix[tempPoint->x][tempPoint->y] = 0; 186 left.y = tempPoint->y; 187 right.y = tempPoint->y; 188 left.x = tempPoint->x; 189 right.x = tempPoint->x; 190 while (numGroupMatrix[left.x][left.y] != 1){ 191 glVertex2i(left.x, left.y); numGroupMatrix[left.x][left.y]=0; 192 left.x--; 193 } 194 while (numGroupMatrix[right.x][right.y] != 1){ 195 glVertex2i(right.x, right.y); numGroupMatrix[right.x][right.y] = 0; 196 right.x++; 197 } 198 for (i = right.x; i >= left.x;i--){ 199 if (numGroupMatrix[i][right.y+1]==-1){ 200 right.y++; 201 right.x = i; 202 Push(s,right); 203 break; 204 } 205 } 206 right.y = tempPoint->y; 207 for (i = right.x; i >= left.x; i--){ 208 if (numGroupMatrix[i][right.y - 1] == -1){ 209 right.y--; 210 right.x = i; 211 Push(s, right); 212 break; 213 } 214 215 } 216 } 217 } 218 void ProcessExcute(){ 219 //1.初始化待填充区域的边界线段端点和种子坐标 220 Point *p = InitPoint(); 221 //2.栅格化边界线段端点表示的待填充区域到像素阵列数组里 222 int **numGroupMatrix = InitPointMatrixByPoint(p); 223 //3.用扫描线算法进行区域填充: 224 scanLineFixArea(numGroupMatrix); 225 } 226 void display(){ 227 glClear(GL_COLOR_BUFFER_BIT); 228 glColor3d(1.0, 0, 0); 229 glBegin(GL_POINTS); 230 ProcessExcute(); 231 glEnd(); 232 glFlush();; 233 } 234 void Init(){ 235 glClearColor(0, 0, 0, 0); 236 glMatrixMode(GL_PROJECTION); 237 glLoadIdentity(); 238 //定义裁剪区域 239 gluOrtho2D(0, 500, 0, 400); 240 } 241 int main(int argc, char *argv[]){ 242 glutInit(&argc, argv); 243 glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB); 244 glutInitWindowPosition(400, 200); 245 glutInitWindowSize(500, 400); 246 glutCreateWindow("扫描线区域填充算法"); 247 Init(); 248 glutDisplayFunc(display); 249 glutMainLoop(); 250 return 0; 251 }
将坐标值扩大20倍:
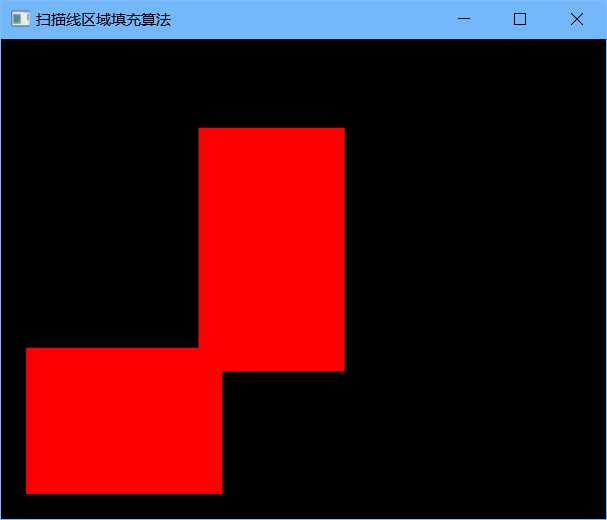
OpenGL学习进程(13)第十课:基本图形的底层实现及算法原理
标签:oop stack rgb str crt 曲线 comm and pmi
原文地址:http://www.cnblogs.com/MenAngel/p/6079548.html