标签:play dom 之间 它的 java 实现 总结 shuffle lan
写在前面的话:
一枚自学Java和算法的工科妹子。
本文是根据《算法(第四版)》的个人总结,如有错误,请批评指正。
一、快速排序介绍
快速排序(Quicksort)是一种分治的排序算法。它将一个数组分成两个数组,将两部分独立地排序,快速排序示意图如下:

与归并排序的区别:
快速算法引人注目的特点就是(1)原地排序;(2)长度N的数组排序所需时间和NlgN成正比,它的内循环比大多数排序算法都要短小,使得排序速度很快。但是主要缺点是非常脆弱,在实现时要非常小心,保持数组的随机性,将输入的待排序数组元素的顺序先打乱过,否则对于已经排好序或是逆序的数组,排序算法需要~N2/2次比较,即运行时间是平方级别的。为了预防这种情况的方法,可以用StdRandom.shuffle()方法打乱数组,这个方法在许多场合会用到,大家可以学习下。
1 public class StdRandom 2 {// 这是一个随机数静态方法库,包含各种随机数生成方法和随机数操作方法 3 ... 4 public static void shuffle(int[] a) { 5 // 参数可以改成其他数据类型double 6 if (a == null) throw new IllegalArgumentException("argument array is null"); 7 int n = a.length; 8 for (int i = 0; i < n; i++) { 9 int r = i + StdRandom.uniform(n-i); 10 //StdRandom.uniform(n-i) 方法随机产生1到n-i之间的整数 11 int temp = a[i]; 12 a[i] = a[r]; 13 a[r] = temp; 14 } 15 } 16 }
二、切分(paetition)
快速排序算法的关键在于切分(paetition),这个过程使得数组满足下面三个条件:
1. 切分(paetition)流程:
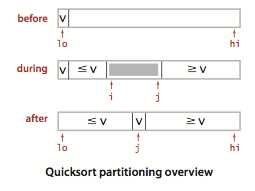
2.切分(paetition)代码实现:
1 private static int partition(Comparable[] a, int lo, int hi) { 2 int i = lo, int j = hi + 1; // 左右扫描指针 3 Comparable v = a[lo]; // 切分元素 4 while (true) 5 { // 扫描左右,检查扫描是否结束并交换元素 6 while (less(a[++i], v)) if (i == hi) break; 7 while (less(v, a[--j]))if (j == lo) break; // 条件(j == lo) 冗余 8 if (i >= j) break; 9 exch(a, i, j); 10 } 11 12 // 将切分元素v放在争取位置a[j] 13 exch(a, lo, j); 14 // 完成a[lo .. j-1] <= a[j] <= a[j+1 .. hi] 15 return j; 16 }
上述代码的优势:
3.切分(paetition)案例图:
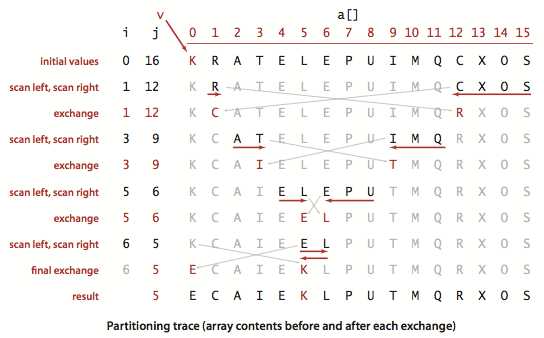
三、快速排序算法的实现
1 public class Quick { 2 3 private Quick() { } 4 5 public static void sort(Comparable[] a) { 6 StdRandom.shuffle(a); //消除对输入的依赖 7 sort(a, 0, a.length - 1); 8 assert isSorted(a); 9 } 10 11 // quicksort the subarray from a[lo] to a[hi] 12 private static void sort(Comparable[] a, int lo, int hi) { 13 if (hi <= lo) return; 14 int j = partition(a, lo, hi); 15 sort(a, lo, j-1); 16 sort(a, j+1, hi); 17 assert isSorted(a, lo, hi); 18 } 19 20 // partition the subarray a[lo..hi] so that a[lo..j-1] <= a[j] <= a[j+1..hi] 21 // and return the index j. 22 private static int partition(Comparable[] a, int lo, int hi) { 23 int i = lo, int j = hi + 1; 24 Comparable v = a[lo]; 25 while (true) { 26 while (less(a[++i], v)) if (i == hi) break; 27 while (less(v, a[--j])) if (j == lo) break; 28 if (i >= j) break; 29 exch(a, i, j); 30 } 31 32 exch(a, lo, j); 33 return j; 34 } 35 36 37 public static Comparable select(Comparable[] a, int k) { 38 if (k < 0 || k >= a.length) { 39 throw new IndexOutOfBoundsException("Selected element out of bounds"); 40 } 41 StdRandom.shuffle(a); 42 int lo = 0, hi = a.length - 1; 43 while (hi > lo) { 44 int i = partition(a, lo, hi); 45 if (i > k) hi = i - 1; 46 else if (i < k) lo = i + 1; 47 else return a[i]; 48 } 49 return a[lo]; 50 } 51 52 private static boolean less(Comparable v, Comparable w) { 53 return v.compareTo(w) < 0; 54 } 55 56 private static void exch(Object[] a, int i, int j) { 57 Object swap = a[i]; a[i] = a[j]; a[j] = swap; 58 } 59 60 private static boolean isSorted(Comparable[] a) { 61 return isSorted(a, 0, a.length - 1); 62 } 63 64 private static boolean isSorted(Comparable[] a, int lo, int hi) { 65 for (int i = lo + 1; i <= hi; i++) 66 if (less(a[i], a[i-1])) return false; 67 return true; 68 } 69 70 private static void show(Comparable[] a) { 71 for (int i = 0; i < a.length; i++) { 72 StdOut.println(a[i]); 73 } 74 } 75 }
快速排序的性能分析:
将长度为N 的数组排序,快速排序平均需要~2NlnN次数组比较,最好情况下是NlgN次数组比较,证明如下:令CN为将N个元素排序平均所需的比较次数

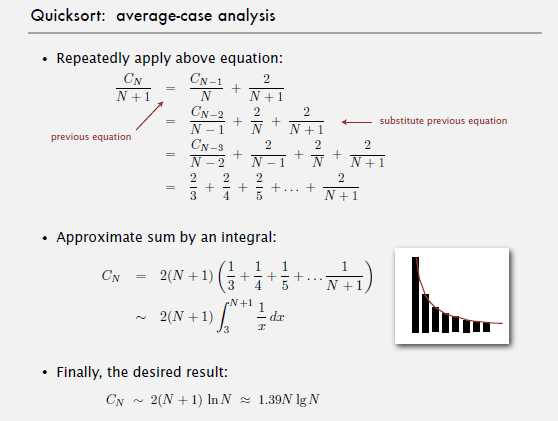
四、快速排序算法的改进
1.切换到插入算法
对于小数组,快速排序比插入排序慢,因为递归,快速排序的sort()方法在小数组中也会调用自己。改进方法:
将sort()中的语句if (hi <= lo) return; 替换成 if (hi <= lo+M) {Insertion.sort(a, lo, hi); return};。
2.三取样切分
使用子数组的一小部分元素的中位数来切分数组。
3.熵最优的排序
将数组切分成三部分,分别对应小于、等于和大于切分元素的数组元素;
Dijkstra“三向切分的排序”:从左到右遍历数组一次,维护一个指针lt使得a[lo..lt-1]中所有元素小于v, 指针gt使得 a[gt+1..hi]中所有元素大于v,指针 i使得a[lt..i-1] 中所有元素等于v,a[i..gt]中的元素都还不确定,方法流程:
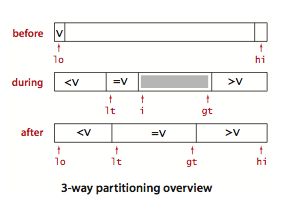
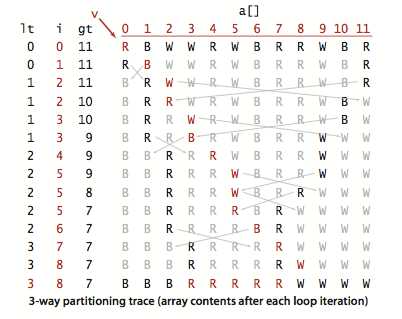
1 public class Quick3way { 2 3 private Quick3way() { } 4 5 public static void sort(Comparable[] a) { 6 StdRandom.shuffle(a); 7 sort(a, 0, a.length - 1); 8 assert isSorted(a); 9 } 10 11 // quicksort the subarray a[lo .. hi] using 3-way partitioning 12 private static void sort(Comparable[] a, int lo, int hi) { 13 if (hi <= lo) return; 14 int lt = lo, gt = hi; 15 Comparable v = a[lo]; 16 int i = lo; 17 while (i <= gt) { 18 int cmp = a[i].compareTo(v); 19 if (cmp < 0) exch(a, lt++, i++); 20 else if (cmp > 0) exch(a, i, gt--); 21 else i++; 22 } 23 24 // a[lo..lt-1] < v = a[lt..gt] < a[gt+1..hi]. 25 sort(a, lo, lt-1); 26 sort(a, gt+1, hi); 27 assert isSorted(a, lo, hi); 28 } 29 30 private static boolean less(Comparable v, Comparable w) { 31 return v.compareTo(w) < 0; 32 } 33 34 private static void exch(Object[] a, int i, int j) { 35 Object swap = a[i];a[i] = a[j];a[j] = swap; 36 } 37 38 private static boolean isSorted(Comparable[] a) { 39 return isSorted(a, 0, a.length - 1); 40 } 41 42 private static boolean isSorted(Comparable[] a, int lo, int hi) { 43 for (int i = lo + 1; i <= hi; i++) 44 if (less(a[i], a[i-1])) return false; 45 return true; 46 } 47 48 private static void show(Comparable[] a) { 49 for (int i = 0; i < a.length; i++) { 50 StdOut.println(a[i]); 51 } 52 } 53 }
作者: 邹珍珍(Pearl_zhen)
出处: http://www.cnblogs.com/zouzz/
声明:本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出 原文链接 如有问题, 可邮件(zouzhenzhen@seu.edu.cn)咨询.
标签:play dom 之间 它的 java 实现 总结 shuffle lan
原文地址:http://www.cnblogs.com/zouzz/p/6098450.html