标签:with art lin 半径 ems 搜索 sum 复杂度 git
1、简介
KNN是一种分类,主要应用领域是对未知事物的识别,即判断未知事物属于哪一类,判断思想是,基于欧几里得定理,判断未知事物的特征和哪一类已知事物的的特征最接近。该方法的思路是:如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。KNN算法中,所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。 KNN方法虽然从原理上也依赖于极限定理,但在类别决策时,只与极少量的相邻样本有关。由于KNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,KNN方法较其他方法更为适合。
2、模型
KNN的三要素是:距离度量,K值选择,分类决策;常用的距离为Lp距离,表达式为: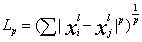 ,当p=1时,为曼哈顿距离,p=2时,为欧氏距离,p为无穷大时
,当p=1时,为曼哈顿距离,p=2时,为欧氏距离,p为无穷大时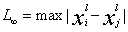 。k值的选择:k越小,近似误差越小,估计误差越大,模型越复杂,过拟合;k值越大,估计误差越小,近似误差越大,模型越简单,欠拟合;k值一般通过交叉验证来获得,一般很小。分类规则,常用的规则是多数表决规则,此时,利用0-1损失,误分类概率为
。k值的选择:k越小,近似误差越小,估计误差越大,模型越复杂,过拟合;k值越大,估计误差越小,近似误差越大,模型越简单,欠拟合;k值一般通过交叉验证来获得,一般很小。分类规则,常用的规则是多数表决规则,此时,利用0-1损失,误分类概率为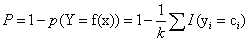 ,使p最小,相当于经验风险最小。
,使p最小,相当于经验风险最小。
实际,一般采用线性扫描和kd树来实现,kd树是一种二叉树,对k维空间进行划分,迭代的利用与坐标轴垂直的平面进行划分,每次划分选择该轴所有数据的中位数进行划分。
kd树应用于KNN中,分为构造过程和搜索过程,构造过程就是依据其划分准则,进行构建二叉树。搜索过程如下:
(1)首先从根节点开始递归往下找到包含 q 的叶子节点,每一层都是找对应的 xi
(2)将这个叶子节点认为是当前的“近似最近点”
(3)递归向上回退,如果以 q 圆心,以“近似最近点”为半径的球与根节点的另一半子区域边界相交,则说明另一半子区域中存在与 q 更近的点,则进入另一个子区域中查找该点并且更新”近似最近点“
(4)重复3的步骤,直到另一子区域与球体不相交或者退回根节点
(5)最后更新的”近似最近点“与 q 真正的最近点
3、总结
从以上简单介绍和对原理的理解可知,KNN的计算复杂度为O(logN),该算法适用于实例数远大于维度数(属性数)。从算法复杂度和效果来分析,KNN是一种相对来说较高效的算法,如下可以分析:目标样本为x,最近邻为z,则出错概率为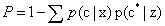 ,用
,用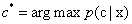 表示贝叶斯最优分类器结果,
表示贝叶斯最优分类器结果,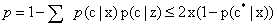 ,KNN的泛化错误率不超过贝叶斯最优分类器的两倍。
,KNN的泛化错误率不超过贝叶斯最优分类器的两倍。
相关博客有:http://blog.csdn.net/jmydream/article/details/8644004,https://my.oschina.net/u/1412321/blog/194174
以下是一些实现的代码:
from numpy import * import operator from os import listdir def classify0(inX, dataSet, labels, k): dataSetSize = dataSet.shape[0] diffMat = tile(inX, (dataSetSize,1)) - dataSet sqDiffMat = diffMat**2 sqDistances = sqDiffMat.sum(axis=1) distances = sqDistances**0.5 sortedDistIndicies = distances.argsort() classCount={} for i in range(k): voteIlabel = labels[sortedDistIndicies[i]] classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1 sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True) return sortedClassCount[0][0] def createDataSet(): group = array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]]) labels = [‘A‘,‘A‘,‘B‘,‘B‘] return group, labels def file2matrix(filename): fr = open(filename) numberOfLines = len(fr.readlines()) #get the number of lines in the file returnMat = zeros((numberOfLines,3)) #prepare matrix to return classLabelVector = [] #prepare labels return fr = open(filename) index = 0 for line in fr.readlines(): line = line.strip() listFromLine = line.split(‘\t‘) returnMat[index,:] = listFromLine[0:3] classLabelVector.append(int(listFromLine[-1])) index += 1 return returnMat,classLabelVector def autoNorm(dataSet): minVals = dataSet.min(0) maxVals = dataSet.max(0) ranges = maxVals - minVals normDataSet = zeros(shape(dataSet)) m = dataSet.shape[0] normDataSet = dataSet - tile(minVals, (m,1)) normDataSet = normDataSet/tile(ranges, (m,1)) #element wise divide return normDataSet, ranges, minVals def datingClassTest(): hoRatio = 0.50 #hold out 10% datingDataMat,datingLabels = file2matrix(‘datingTestSet2.txt‘) #load data setfrom file normMat, ranges, minVals = autoNorm(datingDataMat) m = normMat.shape[0] numTestVecs = int(m*hoRatio) errorCount = 0.0 for i in range(numTestVecs): classifierResult = classify0(normMat[i,:],normMat[numTestVecs:m,:],datingLabels[numTestVecs:m],3) print "the classifier came back with: %d, the real answer is: %d" % (classifierResult, datingLabels[i]) if (classifierResult != datingLabels[i]): errorCount += 1.0 print "the total error rate is: %f" % (errorCount/float(numTestVecs)) print errorCount def img2vector(filename): returnVect = zeros((1,1024)) fr = open(filename) for i in range(32): lineStr = fr.readline() for j in range(32): returnVect[0,32*i+j] = int(lineStr[j]) return returnVect def handwritingClassTest(): hwLabels = [] trainingFileList = listdir(‘trainingDigits‘) #load the training set m = len(trainingFileList) trainingMat = zeros((m,1024)) for i in range(m): fileNameStr = trainingFileList[i] fileStr = fileNameStr.split(‘.‘)[0] #take off .txt classNumStr = int(fileStr.split(‘_‘)[0]) hwLabels.append(classNumStr) trainingMat[i,:] = img2vector(‘trainingDigits/%s‘ % fileNameStr) testFileList = listdir(‘testDigits‘) #iterate through the test set errorCount = 0.0 mTest = len(testFileList) for i in range(mTest): fileNameStr = testFileList[i] fileStr = fileNameStr.split(‘.‘)[0] #take off .txt classNumStr = int(fileStr.split(‘_‘)[0]) vectorUnderTest = img2vector(‘testDigits/%s‘ % fileNameStr) classifierResult = classify0(vectorUnderTest, trainingMat, hwLabels, 3) print "the classifier came back with: %d, the real answer is: %d" % (classifierResult, classNumStr) if (classifierResult != classNumStr): errorCount += 1.0 print "\nthe total number of errors is: %d" % errorCount print "\nthe total error rate is: %f" % (errorCount/float(mTest))
标签:with art lin 半径 ems 搜索 sum 复杂度 git
原文地址:http://www.cnblogs.com/taojake-ML/p/6111424.html