【机器学习经典算法源码分析系列】-- 线性回归

标签：bsp   比较   范围   alt   text   log   手写   课程   and   

一、单变量线性回归：

1.数据集可视化 

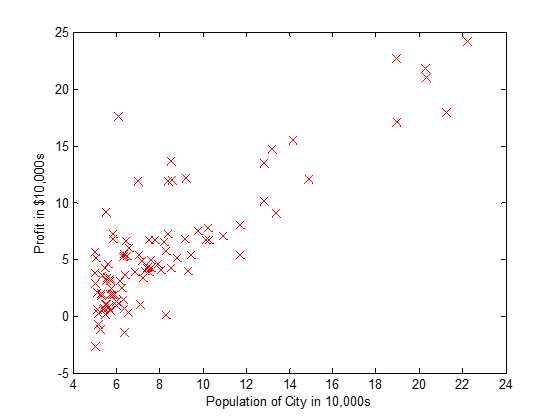
2.求解模型参数

对于线性回归模型，有两种方法可以求解模型参数。

1）  梯度下降法

将代价函数代入展开：

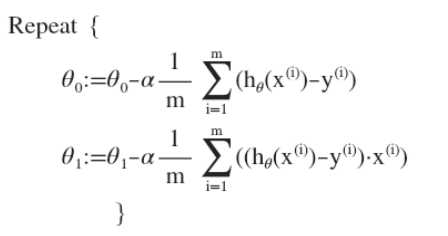
Matlab代码实现：

2）  正规方程

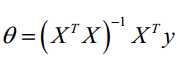
Matlab代码实现：

关于正规方程的推导：

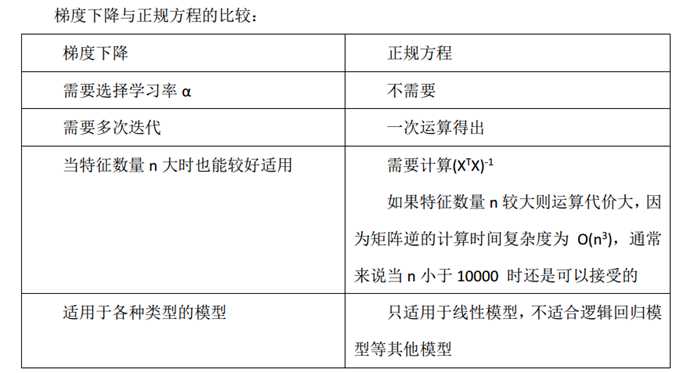
3）梯度下降法和正规方程比较

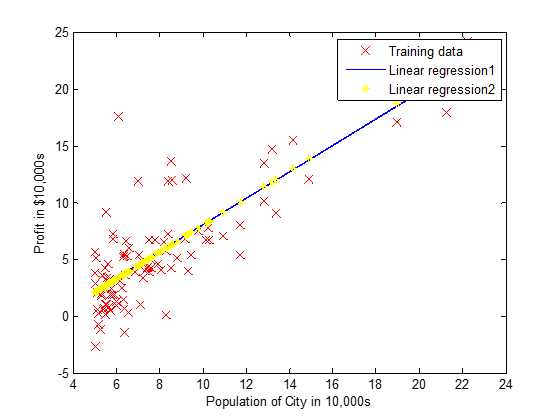
由控制台输出模型参数和回归直线可知，两者得到的结果很相近，具体选择什么方法参照以下标准。

二、多变量线性回归

多变量线性回归求解步骤和单变量线性回归相似，值得注意的一个问题是：

对于多个特征变量，在计算模型参数之前要记得进行特征缩放，使各个特征值大致在同一范围内，有利于进行梯度下降算法求解模型参数。

介绍一种方法如下：

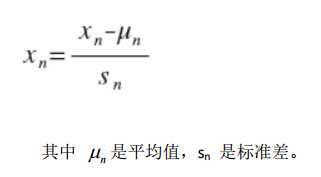
Matlab实现：

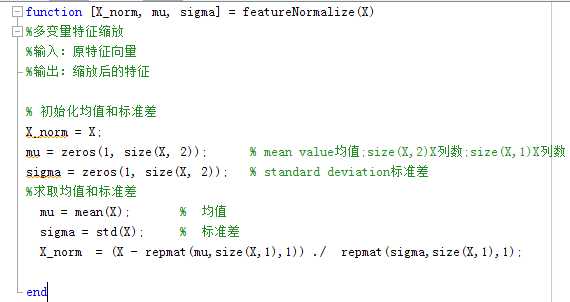
相比较而言，正规方程在处理多变量回归方程问题时省略了特征缩放的步骤，只需按照单变量的步骤进行处理即可，在简洁性上更胜一筹。

三、学习速率的选择

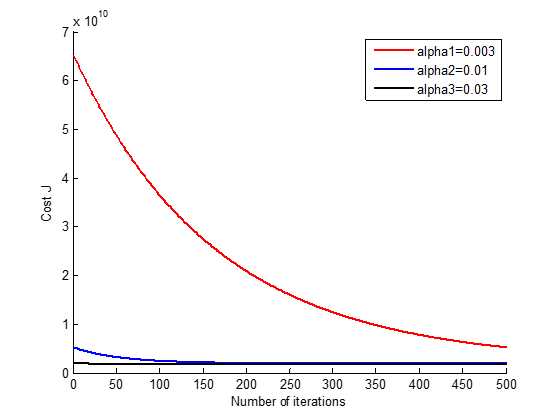
梯度下降法的效率受学习速率的影响非常大，过小，收敛速度非常缓慢，所需迭代次数增大；过大时，每次迭代可能不会减小代价函数，甚至会出现越过局部最小值无法收敛。

可以通过试凑的方式进行的选择：如0.01,0.03,0.1,0.3,1,3,10…

PS:本源码解读针对斯坦福大学机器学习课程（2014版）- 业界大牛Andrew Ng（吴恩民）担任主讲。

PPS：本系列课程笔记【小弟纯手写】：http://www.cnblogs.com/always-chang/p/5935787.html

视频网址：https://www.coursera.org/learn/machine-learning

视频下载：http://pan.baidu.com/s/1dEJcXrj 密码：bnks

源码详细分析：http://pan.baidu.com/s/1bo8rIXL 密码：hdn7

【机器学习经典算法源码分析系列】-- 线性回归

标签：bsp   比较   范围   alt   text   log   手写   课程   and   

原文地址：http://www.cnblogs.com/always-chang/p/6111784.html