标签:基于 珠穆朗玛峰 任务 坐标 介绍 np完全 1.0 span length
最近看到量子退火计算机【D-Ware】研制成功,博主表示十分的兴奋。
我就浅谈一下什么是【模拟退火算法】
----------------------【从爬山算法开始】----------------------------------
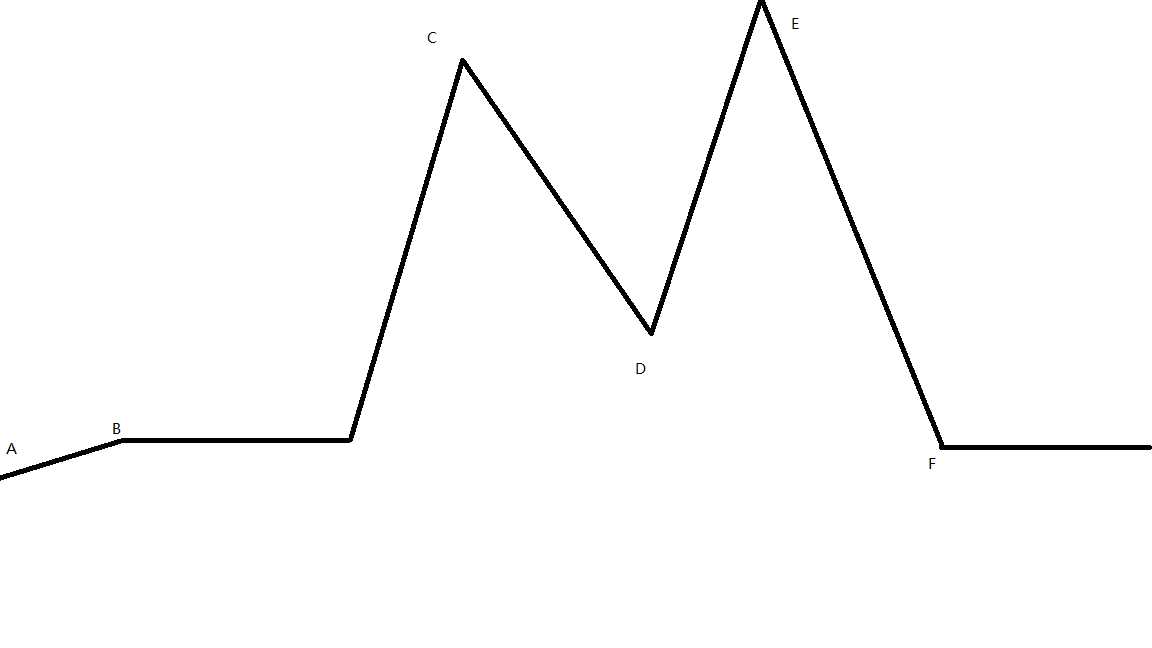
【抱歉,图画的太渣】
好的,我们现在开始假设你在爬这座山,你的任务是在爬完这座山之后告诉我最高的点是哪里。
那么我们用爬山算法的思想来模拟一下。
首先,你来到了A,你心想:这里是我到过最高的地方了(......),所以在当前情况下最优值是A
一会,你来到了B,你发现B好像比A高了一点,于是在当前情况下最高的是B
然后,你发现你的脑容量不够了,为了更加快速,你只能记下左右两个点的高度,所以比较A与B,你忘记了A的高度。
悲催的事情发生了,你走到了C,发现这里真高,应该是世界上最高的地方了,你想左右看了看,发现B与D都没有C高,于是你认为C是这座山最高的点(……)
显而易见,你被局部最优解蒙蔽了双眼……
虽然这种方法对于处理超大规模数据速度很快,但你发现这种算法有着极大的BUG。
------------------------------------【模拟退火算法(SA)】----------------------------------------------------------
那我们如何跳过这个坑呢???
然后我们发现了一种(玄学)算法,既然你的脑容量只足以记住最优两个点的高度,那么我们何不试一试随便左右走走呢?

【再回到这张图】
我们在用退火算法的思想来试一试
首先,你来到了A,你记住了这里的高度。
接着你跳过了B,直接(瞬移???)到了C,你发现这里好像很高,于是你记住了C。
然后你又随机(以一定的概率接受移动,而且这个概率随着时间推移逐渐降低(逐渐降低才能趋向稳定))跳到了D,你发现D真的很矮,但你向右看,你发现了E,于是你忘掉了C和A。
当你来到了E,你接着向F走,你发现F实在太矮了,再向右走你发现没有路了……
经历了 模拟,我们发下模拟退火算法成功的避开了陷入局部最优值的BUG。
这里的“一定的概率”的计算参考了金属冶炼的退火过程,这也是模拟退火算法名称的由来。
那么这个概率如何计算呢:
根据热力学的原理,在温度为T时,出现能量差为dE的降温的概率为P(dE),表示为:
P(dE) = exp( dE/(kT) )
其中k是一个常数,exp表示自然指数,且dE<0。这条公式说白了就是:温度越高,出现一次能量差为dE的降温的概率就越大;温度越低,则出现降温的概率就越小。又由于dE总是小于0(否则就不叫退火了),因此dE/kT < 0 ,所以P(dE)的函数取值范围是(0,1) 。
随着温度T的降低,P(dE)会逐渐降低。
我们将一次向较差解的移动看做一次温度跳变过程,我们以概率P(dE)来接受这样的移动。
让我们打一个形象的比喻:
爬山算法是一个鼠目寸光的人在爬山,他爬到了阿尔卑斯山觉得这是世界上最高的山,但不知道珠穆朗玛峰还在等着他。
模拟退火算法是一个喝醉酒了的人在爬山,他一开始随意的走着,他甚至有可能踏入盆地。但他逐渐清醒,并向高处奔去。
-------------------------------------【SA算法解决实际问题】-------------------------------------------------
SA(模拟退火)算法解决TSP(旅行商问题):有N个城市,唯一遍历所有城市,再回到出发的城市,求最短的路线。
当然SA算法是一种基于随机的算法,它能以非常快的速度获得近似解,有多快呢?O(n)。这个速度已经十分快速了,比起基于枚举的算法要快得多。
那么如何实际解决TSP问题呢?
旅行商问题属于所谓的NP完全问题(不知道的自己百度),精确的解决TSP只能通过穷举所有的路径组合,其时间复杂度是O(N!) 。So,要想尽快的解决TSP请使用SA算法。
使用模拟退火算法可以比较快的求出TSP的一条近似最优路径。(使用遗传算法也是可以的,我将在下一篇文章中介绍)模拟退火解决TSP的思路:
1. 产生一条新的遍历路径P(i+1),计算路径P(i+1)的长度L( P(i+1) )
2. 若L(P(i+1)) < L(P(i)),则接受P(i+1)为新的路径,否则以模拟退火的那个概率接受P(i+1) ,然后降温
3. 重复步骤1,2直到满足退出条件
产生新的遍历路径的方法有很多,下面列举其中3种:
1. 随机选择2个节点,交换路径中的这2个节点的顺序。
2. 随机选择2个节点,将路径中这2个节点间的节点顺序逆转。
3. 随机选择3个节点m,n,k,然后将节点m与n间的节点移位到节点k后面。
代码奉上!!!
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <ctime>//滑稽!!!!!!
const int MAXN = 27; //城市数量
const double MAX = 27.0; //城市数量
const double INIT_T = 3000; //初始温度
const double RATE = 0.95; //温度衰减率
const double FINNAL_T = 1E-10; //终止温度
const int IN_LOOP = 15000; //内循环次数
const int LIMIT = 10000; //概率选择上限
const int FINL_LOOP = 1000; //外层循环
double DD=0;
struct path
{//定义路线结构
int citys[MAXN];
double length;
}D_BestPath;
struct point
{//定义点结构
double x;
double y;
}D_Point[MAXN];
//计算点和点之间的距离
void point_dist()
{
int i, j;
double x;
for(i=0; i<MAXN; i++)
{
for(j=i+1; j<MAXN; j++)
{
x = (D_Point[i].x-D_Point[j].x)*(D_Point[i].x-D_Point[j].x);
x += (D_Point[i].y-D_Point[j].y)*(D_Point[i].y-D_Point[j].y);
D_Length[i][j] = sqrt(x);
D_Length[j][i] = D_Length[i][j];
}
}
}
//初始化
void init()
{
int i;
printf("初始状态路径:");
D_BestPath.length = 0;
for(i=0; i<MAXN; i++)
{//初始顺序经过路径
D_BestPath.citys[i] = i;
printf("%d--", i);
}
for(i=0; i<MAXN-1; i++)
{//计算路径长度
D_BestPath.length += D_Length[i][i+1];
}
printf("\n路径长度为:%.3lf\n\n", D_BestPath.length);
}
void initi()
{ //测试
int i;
D_BestPath.length = 0;
D_BestPath.citys[0] = 0;
D_BestPath.citys[1] = 1;
D_BestPath.citys[2] = 5;
D_BestPath.citys[3] = 4;
D_BestPath.citys[4] = 11;
D_BestPath.citys[5] = 12;
D_BestPath.citys[6] = 3;
D_BestPath.citys[7] = 17;
D_BestPath.citys[8] = 18;
D_BestPath.citys[9] = 19;
D_BestPath.citys[10] = 20;
D_BestPath.citys[11] = 9;
D_BestPath.citys[12] = 13;
D_BestPath.citys[13] = 14;
D_BestPath.citys[14] = 7;
D_BestPath.citys[15] = 6;
D_BestPath.citys[16] = 10;
D_BestPath.citys[17] = 8;
D_BestPath.citys[18] = 2;
D_BestPath.citys[19] = 16;
D_BestPath.citys[20] = 22;
D_BestPath.citys[21] = 21;
D_BestPath.citys[22] = 15;
D_BestPath.citys[23] = 26;
D_BestPath.citys[24] = 25;
D_BestPath.citys[25] = 24;
D_BestPath.citys[26] = 23;
for(i=0; i<MAXN-1; i++)
{//计算路径长度
D_BestPath.length += D_Length[D_BestPath.citys[i]][D_BestPath.citys[i+1]];
}
}
//输入城市坐标信息
void input()
{
int i;
for(i=0; i<MAXN; i++)
scanf("%lf%lf", &D_Point[i].x, &D_Point[i].y);
}
path getnext(path p)
{
path ret;
int i, x, y;
int te;
ret = p;
do
{
x = (int)(MAX*rand()/(RAND_MAX + 1.0));
y = (int)(MAX*rand()/(RAND_MAX + 1.0));
}
while(x == y);
te = ret.citys[x];
ret.citys[x] = ret.citys[y];
ret.citys[y] = te;
ret.length = 0;
for(i=0; i<MAXN-1; i++)
{//计算路径长度
ret.length += D_Length[ret.citys[i]][ret.citys[i+1]];
}
DD++;
return ret;
}
void sa()
{
int i, P_L=0, P_F=0;;
path curPath, newPath;
double T = INIT_T;
double p, delta;
srand((int)time(0));
curPath = D_BestPath;
while(true)
{
for(i=0; i<IN_LOOP; i++)
{
newPath = getnext(curPath);
delta = newPath.length - curPath.length;
if(delta < 0)
{//更新长度
curPath = newPath;
P_L = 0;
P_F = 0;
}
else
{
p = (double)(1.0*rand()/(RAND_MAX+1.0));
if(exp(delta/T) < 1 && exp(delta/T) > p)
{
curPath = newPath;
}
P_L ++;
}
if(P_L > LIMIT)
{
P_F ++;
break;
}
}
if(curPath.length < newPath.length) D_BestPath = curPath;
if(P_F > FINL_LOOP || T<FINNAL_T) break;
T = T * RATE;
}
}
int main()
{
input();
point_dist();
init();
sa();
}
打字真**累……
标签:基于 珠穆朗玛峰 任务 坐标 介绍 np完全 1.0 span length
原文地址:http://www.cnblogs.com/lijiaxin-blog-cpp/p/6115748.html