标签:实现 cpp 黄金分割 block 使用 梯度 想法 min image
目标函数为一元单值函数f:R->R的最小化优化问题,一般不会单独遇到,它通常作为多维优化问题中的一个部分出现,例如梯度下降法中每次最优迭代步长的估计。
一维搜索方法是通过迭代方式求解的,这不同于我们人脑的直接通过解表达式求解方法。迭代算法是从初始搜索点x(0)出发,产生一个迭代序列x(1),x(2),...。在第k=0,1,2,...次迭代中,通过当前迭代点x(k)和目标函数 f 构建下一个迭代点x(k+1)。某些算法可能只需要用到迭代点处的目标函数值,而另一些算法还可能用到目标函数的导数 f‘(x),甚至是二阶导数 f‘‘(x)。
1、问题描述:
如果一元单值函数 f:R->R 在闭区间[a0,b0]上是单峰的, 求解 f 在该区间上的极小点。
2、计算机求解方法:
以下方法的本质是:区间压缩(截取)法,通过不断缩小极小点所在的区间长度到足够的精度水平来逼近极小点。
(1)黄金分割法(每次区间截取比例为固定值)
第一步:初始区间[a0,b0],设定截取比例为 r,则第一次挑选两个中间点 a1和 b1,它们满足对称要求:a1-a0=b0-b1= r(b0-a0),显然 r<1/2,如果 f(a1) < f(b1),那么极小点应该在区间 [a0,b1] 中; 否则,如 f(a1) >= f(b1),极小点应该位于区间 [a1,b0] 中。
第二步:经过第一次压缩后,极小点所在区间变为[a0,b1],或者[a1,b0]。假定为[a0,b1],下面需要第二次挑选中间点 a2和 b2 。为了充分利用第一次的挑选点信息,减少计算次数,那么第二次挑选的点 b2 可以取第一次的挑选点 a1 ,这样就只需要计算b2(即a1)在新区间上的对称点 a2 和 f(a2) 。为了实现这样的想法,那么必须满足下面的要求: r(b1-a0)= b1 - b2=b1-a1 <=> r[b0-r(b0-a0)-a0]=(1-2r)(b0-a0)<=>r2-3r+1=0<=>1-r=(sqrt(5)-1)/2 = 0.618, 即每次截取后保留比例为0.618 故称此方法为黄金分割法。因此 N 步之后,区间长度为(1-r)N=(0.618)N, 即总压缩比。

挑选 a1和 b1 为中间点
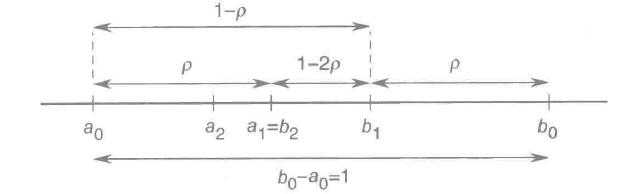
假定第一次截取[b1,b0], 然后在 [a0,b1] 上挑选 a2和 b2,为了减少计算以 a1 取代 b2, 只需计算 a2 。
(2)斐波那契数列法
在黄金分割法进行区间压缩的过程中,参数 r 始终保持不变。如果在允许参数 r 不断调整,比如 第 k 次迭代使用参数 rk,第k+1次迭代使用参数rk+1,以此类推。同时为了减少计算次数,要求每次迭代中只需要计算一次目标函数值(即在每次挑选中间点时,重复利用上一次挑选的一个中间点信息)。那么可以得出下面的等式:
rk+1(1-rk)=1-2rk <=>rk+1=1 - rk/(1-rk)
显然很多序列{rk},0= <rk<=1/2满足上式要求,比如黄金分割法中的序列。因此需要寻找最优的一种序列,使得最终得到的总压缩比达到最小,即(1-r1)(1-r2)...(1-rN)最小。经过数学分析,发现利用斐波那契数列构造数列{rk}={1-FN-k+1/FN-k+2},可以满足上面的要求,其中Fk是斐波那契数列第k个元素,k<=N,N步迭代后使得总压缩比为1//FN+1。
但是可以发现,最后一步迭代rN=1/2, 这就意味着两个中间点aN=bN , 它们位于区间中点上,相互重合,这样将使得区间无法再继续压缩下去。因此需要我们人为调整 rN=1/2 - epsion, epsion是一个很小的正实数。这样最终压缩比可以表示为(1+2*epsion)/FN+1。
算法要求预先设定参数 epsion、最终压缩比,然后求出迭代次数N。注意最后一次迭代使用的rN=1/2 - epsion!
[测试数据]:fx.dat minx.dat
[算法代码]:test.cpp goldseg.a goldseg.so fibonacci.a fibonacci.so
数值算法:无约束优化之一维搜索方法之黄金分割法、斐波那契数列法
标签:实现 cpp 黄金分割 block 使用 梯度 想法 min image
原文地址:http://www.cnblogs.com/xiehbpku/p/6129039.html