标签：之间   正态分布   产生   get   img   技术分享   三维   分解   like   

原文地址：http://ghx0x0.github.io/2014/12/30/NDT-match/

By GH

发表于 12月 30 2014

目前三维配准中用的较多的是ICP迭代算法，需要提供一个较好的初值，同时由于算法本身缺陷，最终迭代结果可能会陷入局部最优。本文介绍的是另一种比较好的配准算法，NDT配准。这个配准算法耗时稳定，跟初值相关不大，初值误差大时，也能很好的纠正过来。

绪论：

• 采样：
  • 3d点云数据在离相机近处点云密度大，远处密度小，所以在下采样时采用统一的采样方法还是会保留密度不均匀；
    一种方法是将空间划分格子，在每个格子内的点云随机取点，点数足够了即可。
  • 短波将会产生更高的分辨率和较少的镜面反射。采用多个深度相机会产生串扰的问题，尤其是镜面反射很厉害的时候。

可以采集图像深度的相机：

1. 雷达radio
2. 激光雷达lidar
   • 三角测量法
   • TOF飞行时间法
   • 相位差法
3. 声呐
4. 双目视觉
   • 双目视觉是一个被动的三角测量；
     缺点：
     A．双目视觉只有能被检测出来的特征点才能检测出深度，在低对比度的环境中，只有很少的特征点能够检测出；
     B．双目视觉的另一个缺点是岁两个相机之间的距离增大，深度精度减少，盲区增大，主要面向几米远的长距离测量。
     C．对于没有纹理的表面检测不出来。
5. 投影光三角测量
6. TOF深度相机
   • 实际上是采用相位偏移法测量；
     TOF深度相机相比lidar的TOF是 采集速度快，硬件便宜
     缺点是噪点很明显，并且需要标定，并且受外界光和本身主动光的影响。 而且曝光时间不容易确定

视图匹配（配准）：

1. ICP
   缺点：

    A．要剔除不合适的点对（点对距离过大、包含边界点的点对）
    B．基于点对的配准，并没有包含局部形状的信息
    C．每次迭代都要搜索最近点，计算代价高昂
   

   存在多种优化了的变体算法，如八叉树等
2. IDC

    ICP的一种改进，采用极坐标代替笛卡尔坐标进行最近点搜索匹配
   

3. PIC

    考虑了点云的噪音和初始位置的不确定性
   

4. Point-based probabilistic registration

    需要首先建立深度图的三角面片
   

5. NDT——正态分布变换：

    计算正态分布是一个一次性的工作（初始化），不需要消耗大量代价计算最近邻搜索匹配点   
    概率密度函数在两幅图像采集之间的时间可以离线计算出来  
   

6. Gaussian fields

    和NDT正态分布变换类似，利用高斯混合模型考察点和点的距离和点周围表面的相似性
   

7. Quadratic patches
8. Likelihood-field matching——随机场匹配
9. CRF匹配

    缺点： 运行速度慢，在3d中实时性能不好，误差大。
   

10. Branch-and-bound registration
11. Registration using local geometric features

NDT算法：

1. 将空间（reference scan）划分成各个格子cell
2. 将点云投票到各个格子

3. 计算格子的正态分布PDF参数

   

4. 将第二幅scan的每个点按转移矩阵T的变换

5. 第二幅scan的点落于reference的哪个 格子，计算响应的概率分布函数

   

6. 求所有点的最优值，目标函数为

PDF可以当做表面的近似表达，协方差矩阵的特征向量和特征值可以表达表面信息（朝向、平整度）
格子内少于3个点，经常会协方差矩阵不存在逆矩阵，所以只计算点数大于5的cell，涉及到下采样方法。

• NDT的优化：
  格子参数最重要，太大导致精度不高，太小导致内存过高，并且只有两幅图像相差不大的情况才能匹配

1. 固定尺寸
2. 八叉树建立，格子有大有小
3. 迭代，每次使用更精细的格子
4. K聚类，有多少个类就有多少个cell，格子大小不一
5. Linked-cell
6. 三线插值 平滑相邻的格子cell导致的不连续，提高精度
   缺点：插值导致时间是普通的4倍
   优点：可以提高鲁棒性

ICP算法：

1. 给定参考点集P和数据点集Q（在给定初始估计RT时）
2. 对Q中的每一个点寻找P中的对应最近点，构成匹配点对
3. 对匹配点对求欧氏距离和作为误差目标函数error
4. 利用SVD分解求出R和T，使得error最小
5. 将Q按照R和T旋转变化，并以此为基准回到1 重新寻找对应点对

NDT 耗时稳定，跟初值相关不大，初值误差大时，也能很好的纠正过来；  
ICP耗时多，容易陷入局部最优；  

可以根据格子cell的PDF的协方差矩阵计算特征向量特征值，每个格子有球形状、平面、线型三种类型，根据朝向作以统计，得到局部或者一幅图像的特征直方图  

文章来自于Martin Magnusson的The Three-Dimensional Normal-Distributions Transform— an Efficient Representation for Registration,Surface Analysis, and Loop Detection。 作者详细介绍了NDT在各个条件下的配准效果及与其他配准方法的详细实验对比，并利用NDT算法配准矿洞内三维场景，同时完成SLAM任务。

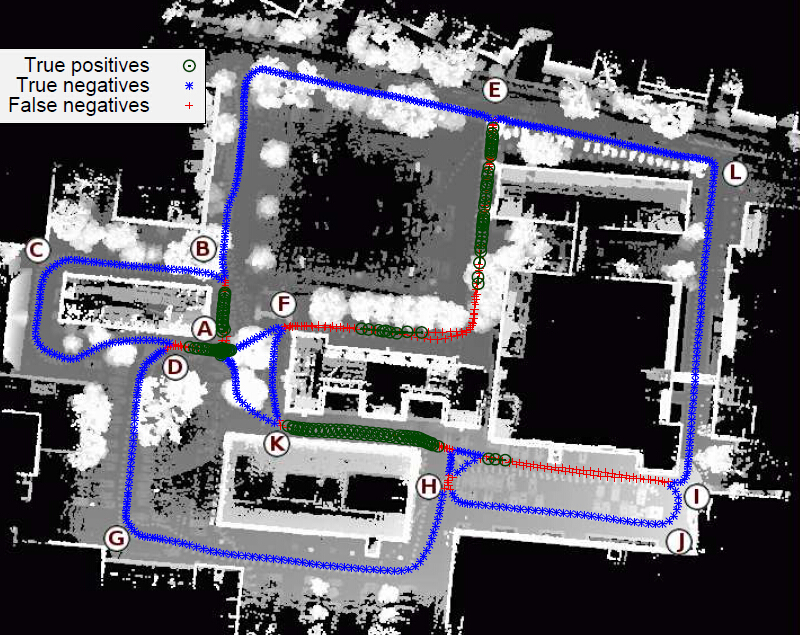
NDT（Normal Distribution Transform） 算法（与ICP对比）和一些常见配准算法

标签：之间   正态分布   产生   get   img   技术分享   三维   分解   like   

原文地址：http://www.cnblogs.com/sddai/p/6129446.html