标签:修改 大小 磁盘 back 路径 tail 文件 比赛 数据
来来来,根据这篇文章,学一下败者树吧:
http://blog.csdn.net/whz_zb/article/details/7425152
一、胜者树
胜者树的一个优点是,如果一个选手的值改变了,可以很容易地修改这棵胜者树。只需要沿着从该结点到根结点的路径修改这棵二叉树,而不必改变其他比赛的结果。
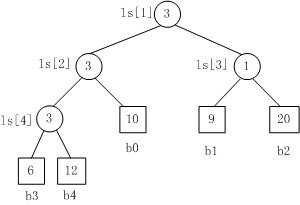
二、败者树
败者树是胜者树的一种变体。在败者树中,用父结点记录其左右子结点进行比赛的败者,而让胜者参加下一轮的比赛。败者树的根结点记录的是败者,需要加一个结点来记录整个比赛的胜利者。采用败者树可以简化重构的过程。
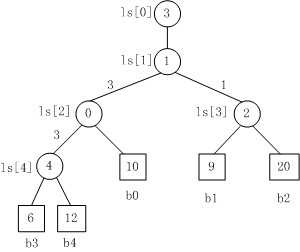
一 外部排序的基本思路
假设有一个72KB的文件,其中存储了18K个整数,磁盘中物理块的大小为4KB,将文件分成18组,每组刚好4KB。
首先通过18次内部排序,把18组数据排好序,得到初始的18个归并段R1~R18,每个归并段有1024个整数。
然后对这18个归并段使用4路平衡归并排序。
第1次归并:产生5个归并段
R11 R12 R13 R14 R15
其中
R11是由{R1,R2,R3,R4}中的数据合并而来
R12是由{R5,R6,R7,R8}中的数据合并而来
R13是由{R9,R10,R11,R12}中的数据合并而来
R14是由{R13,R14,R15,R16}中的数据合并而来
R15是由{R17,R18}中的数据合并而来
把这5个归并段的数据写入5个文件。
类推,下略。
二 使用败者树加快合并排序
外部排序最耗时间的操作时磁盘读写,对于有m个初始归并段,k路平衡的归并排序,磁盘读写次数为
|logkm|,可见增大k的值可以减少磁盘读写的次数,但增大k的值也会带来负面效应,即进行k路合并
的时候会增加算法复杂度。
如果使用败者树,可以在O(logk)的复杂度下得到最小的数,算法复杂度将为O((n-1)*logk), 对于外部排序这种数据量超大的排序来说,这是一个不小的提高。
标签:修改 大小 磁盘 back 路径 tail 文件 比赛 数据
原文地址:http://www.cnblogs.com/charlesblc/p/6138908.html