标签:mil current undle grid 数字 方式 string repeat creat
目录

具体问题即解决方案请参考本人另一篇博客:算法笔记_001:斐波那契数的多种解法
功能界面布局main_one.xml文件对应界面图:
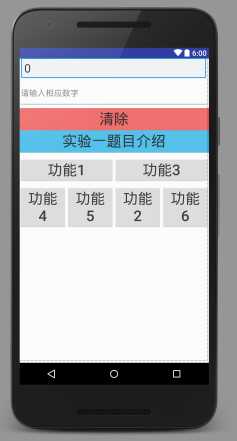
其源码:
<?xml version="1.0" encoding="utf-8" ?> <GridLayout xmlns:android="http://schemas.android.com/apk/res/android" android:layout_width="match_parent" android:layout_height="match_parent" android:rowCount="14" android:columnCount="3" android:id="@+id/root"> <!-- 定义一个横跨4列的文本框, 并设置该文本框的前景色、背景色等属性 --> <ScrollView android:layout_width="match_parent" android:layout_height="wrap_content" android:lines="8"> <TextView android:layout_width="match_parent" android:layout_height="wrap_content" android:singleLine="false" android:marqueeRepeatLimit="marquee_forever" android:ellipsize="marquee" android:scrollHorizontally="true" android:layout_columnSpan="3" android:textSize="25sp" android:layout_marginLeft="2pt" android:layout_marginRight="2pt" android:padding="3pt" android:layout_gravity="right" android:background="#eee" android:textColor="#000" android:text="0" android:id="@+id/show_result" /> </ScrollView> <!-- 定义一个横跨4列的按钮 --> <EditText android:layout_width="match_parent" android:layout_height="wrap_content" android:layout_columnSpan="3" android:lines="2" android:hint="请输入相应数字" android:selectAllOnFocus="true" android:id="@+id/number" /> <Button android:layout_width="match_parent" android:layout_height="wrap_content" android:layout_columnSpan="3" android:textSize="32sp" android:text="清除" android:background="@android:color/holo_blue_light" android:backgroundTint="#ed5454" android:id="@+id/clean" android:onClick="one_clean"/> <Button android:layout_width="match_parent" android:layout_height="wrap_content" android:layout_columnSpan="3" android:textSize="32sp" android:text="实验一题目介绍" android:background="@android:color/holo_blue_light" android:id="@+id/introduce" android:onClick="one_indrouce"/> <LinearLayout android:id="@+id/linearLayout4" android:layout_width="match_parent" android:layout_height="wrap_content" android:orientation="vertical" android:paddingTop="5dip" > <LinearLayout android:id="@+id/linearLayout2" android:layout_width="match_parent" android:layout_height="wrap_content" android:orientation="horizontal" android:paddingTop="5dip" > <Button android:id="@+id/button_one" android:layout_width="wrap_content" android:layout_height="match_parent" android:layout_weight="1" android:text="功能1" android:textSize="32sp" android:onClick="function_one"/> <Button android:id="@+id/button_three" android:layout_width="wrap_content" android:layout_height="match_parent" android:layout_weight="1" android:text="功能3" android:textSize="32sp" android:onClick="function_three"/> </LinearLayout> <LinearLayout android:id="@+id/linearLayout3" android:layout_width="match_parent" android:layout_height="wrap_content" android:orientation="horizontal" android:paddingTop="5dip" > <Button android:id="@+id/button_four" android:layout_width="wrap_content" android:layout_height="match_parent" android:layout_weight="1" android:text="功能4" android:textSize="32sp" android:onClick="function_four"/> <Button android:id="@+id/button_five" android:layout_width="wrap_content" android:layout_height="match_parent" android:layout_weight="1" android:text="功能5" android:textSize="32sp" android:onClick="function_five"/> <Button android:id="@+id/button_two" android:layout_width="wrap_content" android:layout_height="wrap_content" android:layout_weight="1" android:text="功能2" android:textSize="32sp" android:onClick="function_two"/> <Button android:id="@+id/button_six" android:layout_width="wrap_content" android:layout_height="match_parent" android:layout_weight="1" android:text="功能6" android:textSize="32sp" android:onClick="function_six"/> </LinearLayout> </LinearLayout> </GridLayout>
main_one.xml文件对应MainActivity.java文件源码:
package com.liu.zhen.algorithm; import android.app.Activity; import android.content.Intent; import android.graphics.Color; import android.net.Uri; import android.support.v7.app.AppCompatActivity; import android.os.Bundle; import android.view.Gravity; import android.view.View; import android.widget.Button; import android.widget.EditText; import android.widget.GridLayout; import android.widget.TextView; public class MainActivity extends AppCompatActivity{ @Override protected void onCreate(Bundle savedInstanceState) { super.onCreate(savedInstanceState); setContentView(R.layout.main_one); } //用迭代法寻找编程环境支持的最大整数(int型)的斐波那契数是第几个斐波那契数 public static int max_int_iteration(){ int a = 1,b = 1,c = 2; int count = 3; for( ;b < c; ){ //一旦c达到编程环境最大斐波那契数,便会产生内存溢出,从而变成一个负数,到此循环结束 a = b; b = c; c = a + b; count++; } return count; } //用迭代法寻找编程环境支持的最大整数(long型)的斐波那契数是第几个斐波那契数 public static long max_long_iteration() { long a = 1, b = 1, c = 2; long count = 3; for (; b < c; ) { //一旦c达到编程环境最大斐波那契数,便会产生内存溢出,从而变成一个负数,到此循环结束 a = b; b = c; c = a + b; count++; } return count; } //递归法 public static int recursion(int n){ int result = 0; //最后一个斐波那契数及存储中间斐波那契数的变量 if(n <= 0) result = 0; if(n == 1 || n == 2) result = 1; if(n > 2) { result = recursion(n-1) + recursion(n-2); //System.out.print(result+" "); } return result; } //规定时间内,递归法计算出的最大斐波那契数是第几个 public static int recursion_time(long time){ long starttime_dg=System.currentTimeMillis(); int i=3; long endtime_dg=0; while(endtime_dg<starttime_dg+time*1000){ endtime_dg=System.currentTimeMillis(); i++; recursion(i); } return i; } //迭代方法对斐波那契数列求解 public static int iteration(int n){ int a[]=new int[n+1]; a[0]=0;a[1]=1;int result=0; if(n==1) return 1; for(int i=2;i<n+1;i++){ a[i]=a[i-1]+a[i-2]; result=a[n]; } return result; } //规定时间内,迭代法计算出的最大斐波那契数是第几个 public static int iteration_time(long time){ long starttime_dg=System.currentTimeMillis(); int i=3; long endtime_dg=0; while(endtime_dg<starttime_dg+time*1000){ endtime_dg=System.currentTimeMillis(); i++; iteration(i); } return i; } //直接求值法(利用公式F(n) = [@n/sqrt(5)]快速计算第n个斐波那契数) public static double formula(int n){ double result = 0; double temp = Math.sqrt(5.0); result = (1/temp)*(Math.pow((1+temp)/2,n)-Math.pow((1-temp)/2, n)); return result; } //利用直接求值法,出现误差时最小的n值 public static int min_formula(){ double result_fn=1; int i=1; while(result_fn-(double)iteration(i)<1){ result_fn=formula(i); i++; } return i; } // 关联矩阵 private static final int[][] UNIT = { { 1, 1 }, { 1, 0 } }; // 全0矩阵 private static final int[][] ZERO = { { 0, 0 }, { 0, 0 } }; /** * 求斐波那契数列 * * @param n * @return */ public static int[][] fb(int n) { if (n == 0) { return ZERO; } if (n == 1) { return UNIT; } // n是奇数 if ((n & 1) == 0) { int[][] matrix = fb(n >> 1); return matrixMultiply(matrix, matrix); } // n是偶数 int[][] matrix = fb((n - 1) >> 1); return matrixMultiply(matrixMultiply(matrix, matrix), UNIT); } /** * 矩阵相乘 * * @param m * r1*c1 * @param n * c1*c2 * @return 新矩阵,r1*c2 */ public static int[][] matrixMultiply(int[][] m, int[][] n) { int rows = m.length; int cols = n[0].length; int[][] r = new int[rows][cols]; for (int i = 0; i < rows; i++) { for (int j = 0; j < cols; j++) { r[i][j] = 0; for (int k = 0; k < m[i].length; k++) { r[i][j] += m[i][k] * n[k][j]; } } } return r; } //具体实现矩阵相乘算法 public static int matrix(int n){ int[][] m = fb(n); return m[0][1]; } //清除 public void one_clean(View v) { String clean_text = "0"; TextView show_text = (TextView) findViewById(R.id.show_result); show_text.setText(clean_text); } //题目介绍 public void one_indrouce(View v) { Intent intent = new Intent(); intent.setClass(MainActivity.this,MainOneActivity.class); startActivity(intent); } //功能1 public void function_one(View v) { int a = max_int_iteration(); long b = max_long_iteration(); String function_one = "迭代法编程环境支持的最大整数(int型)值:" + a + "\n" + "迭代法编程环境支持的" + "最大整数(long型)值:" + b; TextView show_text = (TextView) findViewById(R.id.show_result); show_text.setText(function_one); } //功能2 public void function_two(View v){ TextView show_text = (TextView) findViewById(R.id.show_result); String wait_two = "请耐心等待......"; show_text.setText(wait_two); int a = 40; long starttime_dg=System.currentTimeMillis(); recursion(a); long endtime_dg=System.currentTimeMillis(); double time = (endtime_dg - starttime_dg)/1000.0; String time_two = "递归方式计算第"+a+"个斐波那契数(int型)耗时:"+time+"秒"; show_text.setText(time_two); // EditText edit_text = (EditText) findViewById(R.id.number); // show_text.setText(time_two); } //功能3 public void function_three(View v){ EditText edit_text = (EditText) findViewById(R.id.number); int t = Integer.parseInt(edit_text.getText().toString()); int a = recursion_time(t); int b = iteration_time(t); String three_function = "递归法在"+t+"秒内计算出的最大斐波那契数是第"+a+"个"+"\n"+"迭代法在"+t+"秒内" + "计算出的最大斐波那契数是第"+b+"个"; TextView show_text = (TextView) findViewById(R.id.show_result); show_text.setText(three_function); } //功能4 public void function_four(View v){ int a = min_formula(); String four_function = "利用直接求值法,出现误差时最小的n值是:"+a; TextView show_text = (TextView) findViewById(R.id.show_result); show_text.setText(four_function); } //功能5 public void function_five(View v){ EditText edit_text = (EditText) findViewById(R.id.number); int t = Integer.parseInt(edit_text.getText().toString()); int a = matrix(t); String five_function = "利用矩阵相乘法计算第"+t+"个斐波那契数的值是:"+a; TextView show_text = (TextView) findViewById(R.id.show_result); show_text.setText(five_function); } //功能6 public void function_six(View v){ EditText edit_text = (EditText) findViewById(R.id.number); int t = Integer.parseInt(edit_text.getText().toString()); //迭代法计算耗时 long starttime_iteration=System.currentTimeMillis(); int a1 = iteration(t); long endtime_iteration=System.currentTimeMillis(); double time_iteration = (endtime_iteration-starttime_iteration)/1000.0; // long time_iteration = six_time_iteration(t); String b1 = "迭代法计算第"+t+"个斐波那契数耗时:"+time_iteration+"秒 计算结果是:"+a1; //递归法计算耗时 long starttime_recursion=System.currentTimeMillis(); int a2 = recursion(t); long endtime_recursion=System.currentTimeMillis(); double time_recursion = (endtime_recursion-starttime_recursion)/1000.0; String b2 = "递归法计算第"+t+"个斐波那契数耗时:"+time_recursion+"秒 计算结果是:"+a2; //公式法计算耗时 long starttime_formula=System.currentTimeMillis(); double a3 = formula(t); long endtime_formula=System.currentTimeMillis(); double time_formula = (endtime_formula-starttime_formula)/1000.0; String b3 = "公式法计算第"+t+"个斐波那契数耗时:"+time_formula+"秒 计算结果是:"+(int)a3; //矩阵相乘法计算耗时 long starttime_matrix=System.currentTimeMillis(); int a4 = matrix(t); long endtime_matrix=System.currentTimeMillis(); double time_matrix = (endtime_matrix-starttime_matrix)/1000.0; String b4 = "矩阵相乘法计算第"+t+"个斐波那契数耗时:"+time_matrix+"秒 计算结果是:"+a4; String six_function = b1+"\n"+b2+"\n"+b3+"\n"+b4; TextView show_text = (TextView) findViewById(R.id.show_result); show_text.setText(six_function); } }
具体问题即解决方案请参考本人另一篇博客:算法笔记_002:最近点对问题
功能界面布局activity_maintwo.xml文件对应界面图:
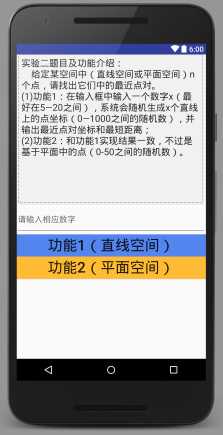
其源码:
<?xml version="1.0" encoding="utf-8"?> <GridLayout xmlns:android="http://schemas.android.com/apk/res/android" android:layout_width="match_parent" android:layout_height="match_parent" android:rowCount="17" android:columnCount="3" android:id="@+id/root"> <!-- 定义一个横跨11列的文本框, 并设置该文本框的前景色、背景色等属性 --> <TextView android:layout_width="match_parent" android:layout_height="wrap_content" android:singleLine="false" android:marqueeRepeatLimit="marquee_forever" android:ellipsize="marquee" android:scrollHorizontally="true" android:layout_columnSpan="3" android:lines="13" android:textSize="20sp" android:layout_marginLeft="2pt" android:layout_marginRight="2pt" android:padding="3pt" android:layout_gravity="right" android:background="#eee" android:textColor="#000" android:text="实验二题目及功能介绍:\n 给定某空间中(直线空间或平面空间)n个点,请找出它们中的最近点对。\n(1)功能1:在输入框中输入一个数字x(最好在5—20之间),系统会随机生成x个直线上的点坐标(0—1000之间的随机数),并输出最近点对坐标和最短距离;\n(2)功能2:和功能1实现结果一致,不过是基于平面中的点(0-50之间的随机数)。" android:id="@+id/show_two" /> <!-- 定义一个横跨2列的输入文本框 --> <EditText android:layout_width="match_parent" android:layout_height="wrap_content" android:layout_columnSpan="3" android:lines="2" android:hint="请输入相应数字" android:selectAllOnFocus="true" android:id="@+id/number_two" /> <!-- 定义一个两个功能键按钮 --> <Button android:layout_width="match_parent" android:layout_height="wrap_content" android:layout_columnSpan="3" android:textSize="32sp" android:text="功能1(直线空间)" android:background="@android:color/holo_blue_light" android:backgroundTint="#5484ed" android:id="@+id/function_line" android:onClick="function_line"/> <Button android:layout_width="match_parent" android:layout_height="wrap_content" android:layout_columnSpan="3" android:textSize="32sp" android:text="功能2(平面空间)" android:background="@android:color/holo_blue_light" android:id="@+id/function_space" android:onClick="function_space" android:backgroundTint="@android:color/holo_orange_light" /> </GridLayout>
activity_maintwo.xml对应Main2Activity.java文件源码:
package com.liu.zhen.algorithm; import android.content.Intent; import android.support.v7.app.AppCompatActivity; import android.os.Bundle; import android.view.View; import android.widget.EditText; public class Main2Activity extends AppCompatActivity { @Override protected void onCreate(Bundle savedInstanceState) { super.onCreate(savedInstanceState); setContentView(R.layout.activity_maintwo); } //初始化一个随机数组 public static int[] initializationArray(int n){ int[] result = new int[n]; for(int i = 0;i < n;i++) result[i] = (int)(Math.random()*1000); //采用随机函数随机生成0~1000之间的数 return result; } //返回数组中最大值 public static int getArrayMax(int a[] , int first , int end){ int max = a[first]; for(int i = first;i < end;i++){ if(max < a[i]) max = a[i]; } return max; } //返回数组中最小值 public static int getArrayMin(int a[] , int first , int end){ int min = a[first]; for(int i = first;i < end;i++){ if(min > a[i]) min = a[i]; } return min; } //交换数组a[n]中两个数的值 public static void swapArray(int a[] , int i , int j){ int temp = a[i]; a[i] = a[j]; a[j] = temp; } //采用分治法将数组a[n]分成两组,满足a[n1]<m,a[n2]>m(其中n1+n2 = n) public static int divideArray(int a[],int first,int end){ int max = getArrayMax(a,first,end); int min = getArrayMin(a,first,end); double m = (max + min)/2.0; //System.out.println("分治法算出中位数m:"+m); int i = first , j = end-1; //int a1 = 0; for( ;i+1 <= j;){ while(a[i] < m && i+1 <= j) i++; while(a[j] > m && i+1 <= j) j--; // a1++; // System.out.println("第"+a1+"此交换时a[i] = "+a[i]+" i = "+i+" a[j] = "+a[j]+" j = "+j); swapArray(a,i,j); //a[i]大于m的值与a[j]小于m的值进行交换,但数组的位置不变 } //System.out.println("分组后,返回的序号j值是:"+(j)); return j; } //采用递归法合并最短距离值,返回最短距离的点 public static int[] getMinDistancePoint(int a[] , int result[],int n ,int first , int end) { if(end-first <= 1){ //递归终止条件 return result; } int j = divideArray(a,first,end); int minDistance = result[1] - result[0]; //最短距离两点之间的距离大小 if(minDistance > getArrayMin(a,j,end)-getArrayMax(a,first,j)) { result[0] = getArrayMax(a,first,j); //最短距离两点中数值最小的点 result[1] = getArrayMin(a,j,end); //最短距离两点中数值最小的点 } int result_one[] = getMinDistancePoint(a,result,2,first,j); //递归 int minDistance_one = result_one[1] - result_one[0]; int result_two[] = getMinDistancePoint(a,result,2,j,end); //递归 int minDistance_two = result_two[1] - result_two[0]; if(minDistance > minDistance_one) result = result_one; if(minDistance > minDistance_two) result = result_two; return result; } //平面中求两点最短距离问题解法 //初始化一个平面中n个点,具体点的坐标值随机生成 public static Point[] initializationPlaneArray(int n){ Point result[] = new Point[n]; for(int i = 0;i < n;i++){ int x1 = (int)(Math.random()*50); //采用随机函数随机生成1~100之间的数 int y1 = (int)(Math.random()*50); result[i] = new Point(x1,y1); } return result; } //迭代法直接求平面中两点之间的最短距离,返回最短距离的两点坐标 public static Point[] getMinDistancePlanePoint(Point a[],int n){ Point result[] = new Point[2]; double min = 10000; //定义两点之间最短距离变量,初始化为10000 for(int i = 0;i < n;i++){ int x = a[i].getX(); int y = a[i].getY(); for(int j = i+1;j < n;j++){ int x1 = a[j].getX(); int y1 = a[j].getY(); long minSquare = (x-x1)^2 + (y-y1)^2; //利用数学中求两点之间距离公式,得到两点之间距离的平方 double min1 = Math.sqrt(minSquare); //求两点之间距离的中间变量 if(min > min1){ min = min1; result[0] = new Point(x,y); result[1] = new Point(x1,y1); } } } return result; } //功能1(直线空间) public void function_line(View v){ EditText edit_text = (EditText) findViewById(R.id.number_two); int t = Integer.parseInt(edit_text.getText().toString()); int a[] = new int[t]; int b[] = new int[2]; b[0] = 0; b[1] = 1000; a = initializationArray(t); String one_text = ""; for(int i = 0;i < t;i++) one_text += "直线随机点Point["+i+"] = "+a[i]+"\n"; int result[] = getMinDistancePoint(a,b,2,0,t); one_text += "最短距离点对第1点result[0] = "+result[0]+"\n"+"最短距离点对第2点result[1] = "+result[1]; //System.out.print(one_text); Intent intent = new Intent(); Bundle bundle = new Bundle(); bundle.putString("str",one_text); intent.putExtras(bundle); intent.setClass(Main2Activity.this,TwoResultActivity.class); startActivity(intent); } //功能2(平面空间) public void function_space(View v){ EditText edit_text = (EditText) findViewById(R.id.number_two); int t = Integer.parseInt(edit_text.getText().toString()); String two_text = ""; Point c[] = initializationPlaneArray(t); for(int i = 0;i < t;i++) two_text += "平面随机点Point["+i+"] = "+"("+c[i].getX()+","+c[i].getY()+")"+"\n"; Point back[] = getMinDistancePlanePoint(c,t); for(int i = 0;i < 2;i++) two_text += "距离最短的两点第"+(i+1)+"个点坐标是:"+"("+back[i].getX()+","+back[i].getY()+")"+"\n"; Intent intent = new Intent(); Bundle bundle = new Bundle(); bundle.putString("str",two_text); intent.putExtras(bundle); intent.setClass(Main2Activity.this,TwoResultActivity.class); startActivity(intent); } }
附本项目源码:
https://coding.net/u/LiuZhen1995/p/MyDemo/git/tree/origin_six/
标签:mil current undle grid 数字 方式 string repeat creat
原文地址:http://www.cnblogs.com/liuzhen1995/p/6159900.html