标签:make 标准 9.png pixel http 空间 lda led 属性
K-means(K均值)是基于数据划分的无监督聚类算法。
一、基本原理
聚类算法可以理解为无监督的分类方法,即样本集预先不知所属类别或标签,需要根据样本之间的距离或相似程度自动进行分类。聚类算法可以分为基于划分的方法、基于联通性的方法、基于概率分布模型的方法等,K-means属于基于划分的聚类方法。
基于划分的方法是将样本集组成的矢量空间划分为多个区域{Si}i=1k,每个区域都存在一个区域相关的表示{ci}i=1k,通常称为区域中心。对于每个样本,可以建立一种样本到区域中心的映射q(x):
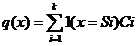
其中1()为指示函数。
根据建立的映射q(x),可以将所有样本分类到相应的中心{ci}i=1k,得到最终的划分结果。如下图所示:
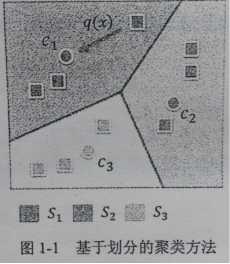
不同的基于划分的聚类算法的主要区别在于如何建立相应的映射方式q(x)。在经典的K-means算法中,映射是通过样本与各中心之间的误差平方和最小准则来建立的。
假设有样本集合D={xj}j=1n,xj∈Rd,K-means聚类算法的目标是将数据集划分为k(k<n)类:S={S1,S2,...,Sk},使划分后的k个子集合满足类内的误差平方和最小:
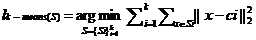
其中: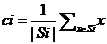
求解目标函数 是一个经典的NP-hard问题,无法保证得到一个稳定的全局最优解。在Sturat Lloyd所提出的经典K-means聚类算法中,采取迭代优化策略,有效地求解目标函数的局部最优解。算法包括样本分配、更新聚类中心等4个步骤。
是一个经典的NP-hard问题,无法保证得到一个稳定的全局最优解。在Sturat Lloyd所提出的经典K-means聚类算法中,采取迭代优化策略,有效地求解目标函数的局部最优解。算法包括样本分配、更新聚类中心等4个步骤。
1.初始化聚类中心c1(0),c2(0),...,ck(0),可选取样本集的前k个样本或者随机选取k个样本;
2.分配各样本xj到相近的聚类集合,样本划分依据为:
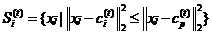
式中i=1,2,...,k,p≠j。
3.根据步骤2的分配结果,更新聚类中心:
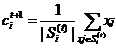
4.若迭代达到最大迭代步数或者前后两次迭代的差小于设定阈值ε,即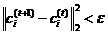 ,则算法结束;否则重复步骤2.
,则算法结束;否则重复步骤2.
K-means聚类算法中的步骤2和步骤3分别对样本集合进行重新分配和重新计算聚类中心,通过迭代计算过程优化目标函数 ,实现类内误差平方和最小。
,实现类内误差平方和最小。
二、算法改进
2.1 算法的计算复杂度分析
首先,在样本分配阶段,需要计算kn次误差平方和,计算复杂度为O(knd).其次,在更新聚类中心阶段,计算复杂度为O(nd)。如果迭代次数为t,则算法的计算复杂度为O(kndt).因此K-means针对样本个数n具有线性的计算复杂度,是一种非常有效的大数据聚类算法。其中:
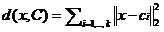
2.2 聚类中心初始化的改进
K-means对聚类中心的初始化比较敏感,不同初始化会带来不同的聚类结果,这是因为K-means仅仅是对目标函数 求取近似局部最优解,不能保证得到全局最优解
求取近似局部最优解,不能保证得到全局最优解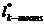 ,即在一定数据分布下聚类结果会因为初始化的不同产生很大偏差。
,即在一定数据分布下聚类结果会因为初始化的不同产生很大偏差。
在标准初始化K-means中,初始聚类中心采用随机采样方式,不能保证得到期望的聚类结果。为了获得较好的聚类结果,可以多次随机初始化聚类中心,得到多组结果进行对比和选择。这么做会大大影响计算时间。
简单有效的改进方式是David Arthur提出的K-means++算法,该算法能够有效产生初始的聚类中心,保证初始化后的K-means可以得到O(logk)的近似解,其理论证明可以参考文献。首先随机初始化一个聚类中心C={ci};然后通过迭代计算最大概率值:
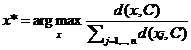
加入下一个聚类中心:
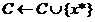
直到选择k个中心。
K-means++算法的计算复杂度为O(knd),没有增加过多的计算负担,同时可以保证算法更有效地近似于最优解。
2.3 类别个数的自适应确定
在经典的K-means算法中,聚类个数k需要预先设定,不具备自适应选择能力,算法的每一步迭代都会单调地降低目标函数 ,在保持类别个数不变的前提下对样本空间进行重新划分得到{Si}i=1k。
,在保持类别个数不变的前提下对样本空间进行重新划分得到{Si}i=1k。
聚类算法中类别个数设定将会在很大程度上决定聚类效果,该参数根据自身的先验知识或启发式来确定,如事先已经知道样本的大体分布或者知道样本中包含的属性个数,如数字、性别类型的样本等。那么如何在算法中加入自适应决定类别个数的过程?
经典方法是ISODATA算法,该算法与K-means在基本原则上一致,通过计算误差平方和最小来实现聚类。但是ISODATA算法在迭代过程中引入类别的合并与分开机制。
在每一次迭代中,ISODATA算法首先在固定类别个数的情况下进行聚类,然后根据设定样本之间的距离阈值进行合并操作,并根据每一组类别Si中的样本协方差矩阵信息来判断是否分开。
ISODATA算法在K-means迭代过程加入附加的启发式重初始化,相比经典的K-means,计算效率会大大降低。
2.4 面向非标准正态分布或非均匀样本集的算法改进
经典的K-means采取二次欧式距离作为相似性度量,并且假设 中的误差服从标准的正态分布。因此,K-means在处理非标准正态分布和非均匀样本集合时聚类效果较差。
中的误差服从标准的正态分布。因此,K-means在处理非标准正态分布和非均匀样本集合时聚类效果较差。
如图所示,针对非标准正态分布和非均匀样本集时,K-means聚类不能得到预期结果,原因在于假设相似度度量为二次欧式距离,在实际的样本集合中该假设不一定都会适用。
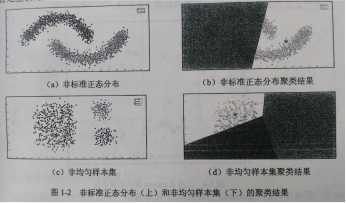
为了有效克服该局限性假设,K-means需要推广到更广义的度量空间,经典的两种改进框架为Kernel K-means和谱聚类Spectral Clustering.
Kernel K-means将样本点xi通过某种映射方式xi->Φ(xi)到新的高维空间Φ,在该空间中样本点之间的内积可以通过对应的核函数进行计算,即:k(xi,xj)=Φ(xi)TΦ(xj)
借助核函数的存在,可以在新空间进行K-means聚类,样本之间的相似性度量就取决与核函数的选择。
谱聚类算法尝试着变换样本的度量空间,首先需要求取样本集合的仿射矩阵,然后计算仿射矩阵的特征向量,利用得到特征向量进行K-means聚类。仿射矩阵的特征向量隐含地重新定义样本定的相似性。
2.5 二分K-means聚类
按照K-means聚类规则很容易陷入局部最小值,马尔科夫随机场中配置的代价函数不是好的目标函数,为了解决该问题,有人提出K-means聚类算法。首先把所有样本作为一个簇,然后二分该簇,接着选择其中一个簇继续进行二分。选择哪一个簇二分的原则就是能否使得误差平方和尽可能小。该算法有了好的目标函数,SSE的计算其实就是距离和。
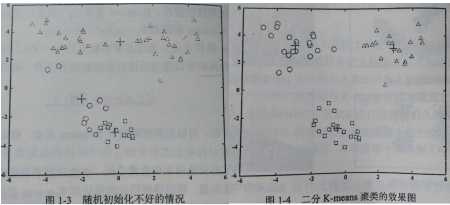
图1-3是K-means算法在随机初始化不好的情况下聚类的效果。采用二分K-means聚类得到的效果如图1-4所示。
三、仿真实验
3.1 基于K-means的图像分割
首先对原始彩色图像进行颜色空间转换,从RGB通道转为Lab颜色空间。
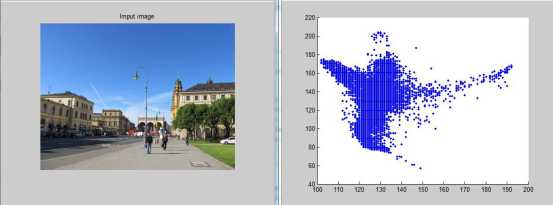
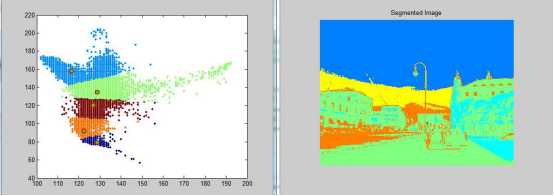
然后在二维的ab通道建立图像像素点,如图1-5所示,测试图像大小为300X400,可以得到2X120000的样本集合,样本分布情况如图1-5(c)所示。
接着对该样本集合利用K-means进行聚类,采用K-means++进行初始化。当设定类别个数k=5时,可以得到如图1-5(b)所示的分割结果,每一种颜色代表不同的聚类类别。
K-means有效地根据图像的颜色信息对图像的不同全区域进行标记,如天空、地面、建筑物等。

%实现如何利用Kmeans聚类实现图像的分割; function kmeans_demo1() clear;close all;clc; %% 读取测试图像 im = imread(‘city.jpg‘); imshow(im), title(‘Imput image‘); %% 转换图像的颜色空间得到样本 cform = makecform(‘srgb2lab‘); %%rgb空间转换成L*a*b*空间结构 lab = applycform(im,cform); %%rgb空间转换成L*a*b*空间 ab = double(lab(:,:,2:3)); %%把I_lab(:,:,2:3)转变为double类型数据 nrows = size(lab,1); ncols = size(lab,2);%计算lab的维数,输出一行向量[m n p]% X = reshape(ab,nrows*ncols,2)‘; %改变矩阵的列数和行数,但是数据总个数不变 figure, scatter(X(1,:)‘,X(2,:)‘,3,‘filled‘); % box on; %显示颜色空间转换后的二维样本空间分布 %scatter可用于描绘散点图。 %1.scatter(X,Y) %X和Y是数据向量,以X中数据为横坐标,以Y中数据位纵坐标描绘散点图,点的形状默认使用圈。 %2.scatter(...,‘filled‘) %描绘实心点。 %3.scatter3(x,y,z) %描绘三维图像。 %print -dpdf 2D1.pdf %% 对样本空间进行Kmeans聚类 k = 5; % 聚类个数 max_iter = 100; %最大迭代次数 [centroids, labels] = run_kmeans(X, k, max_iter); %% 显示聚类分割结果 figure, scatter(X(1,:)‘,X(2,:)‘,3,labels,‘filled‘); %显示二维样本空间聚类效果 hold on; scatter(centroids(1,:),centroids(2,:),60,‘r‘,‘filled‘) hold on; scatter(centroids(1,:),centroids(2,:),30,‘g‘,‘filled‘) box on; hold off; %print -dpdf 2D2.pdf pixel_labels = reshape(labels,nrows,ncols); rgb_labels = label2rgb(pixel_labels); figure, imshow(rgb_labels), title(‘Segmented Image‘); %print -dpdf Seg.pdf end function [centroids, labels] = run_kmeans(X, k, max_iter) % 该函数实现Kmeans聚类 % 输入参数: % X为输入样本集,dxN % k为聚类中心个数 % max_iter为kemans聚类的最大迭代的次数 % 输出参数: % centroids为聚类中心 dxk % labels为样本的类别标记 %% 采用K-means++算法初始化聚类中心 centroids = X(:,1+round(rand*(size(X,2)-1)))%四舍五入取整 labels = ones(1,size(X,2)); %产生大小为1行,size(x,2)列的矩阵,矩阵元素都是1。 %size(x,2)表示x的列数;假设所有样本标记为1 for i = 2:k %5个聚类个数 D = X-centroids(:,labels); D = cumsum(sqrt(dot(D,D,1)));%dot(A,B,DIM)将返回A和B在维数为DIM的点积, %cumsum计算一个数组各行的累加值 if D(end) == 0, centroids(:,i:k) = X(:,ones(1,k-i+1)); return; end centroids(:,i) = X(:,find(rand < D/D(end),1)); [~,labels] = max(bsxfun(@minus,2*real(centroids‘*X),dot(centroids,centroids,1).‘)); end %% 标准Kmeans算法 for iter = 1:max_iter for i = 1:k, l = labels==i; centroids(:,i) = sum(X(:,l),2)/sum(l); end [~,labels] = max(bsxfun(@minus,2*real(centroids‘*X),dot(centroids,centroids,1).‘),[],1); end end
3.2 基于K-means的字典学习
在视觉的特征学习算法中,字典学习是关键步骤,K-means算法可以看成一种最为基本的字典学习方法。
首先从测试灰度图像中收集10000张6x6大小的图像小片(Patches);然后按照文献的建议对所有图像小片进行白化操作;最后,将所有图像小片作为样本集合,利用K-means进行聚类,那么聚类的中心便可作为字典元素。
如图1-6所示,学习到的字典元素类似于Gabor小波基,可以有效地刻画图像的边缘信息,因此K-means是一种有效的字典学习方式。

四、算法特点
K-means聚类算法是最为经典的机器学习方法之一,其目的在于把输入的样本向量分为k个组,求每组的聚类中心,使每组的聚类中心,使非相似性(距离)指标的价值函数(目标函数)最小。
K-means聚类简洁快速,假设均方误差是计算群组分散度的最佳参数,对于满足正态分布的数据聚类效果很好。可应用于机器学习、数据挖掘、模式识别、图像分析和生物信息学等。
K-means的性能依赖于聚类中心的初始位置,不能确保收敛于最优解,对孤立点敏感。可以采用一些前端方法,首先计算出初始聚类中心,或者每次用不同的初始聚类中心将算法运行多次,然后择优确定。
虽然二分K-means聚类算法改进了K-means的不足,但是它们共同的缺点就是必须实现确定K的值,不合适的k可能返回较差结果。对于海量数据,如何确定K的值是学术界一直在研究的问题,常用方法是层次聚类,或者借鉴LDA聚类分析。
参考书籍:视频机器学习20讲及其配套代码
标签:make 标准 9.png pixel http 空间 lda led 属性
原文地址:http://www.cnblogs.com/xiaotongtt/p/6182835.html